4 Properties of \(\mathbb{R}\)
Now that we established the axiomatic definition of the Real Numbers \(\mathbb{R}\) as a complete ordered field, let us investigate some of the properties of \(\mathbb{R}\). These will be consequence of the axioms of the real numbers, particulaly of the Axiom of Completeness.
4.1 Archimedean Property
The Archimedean property is one of the most useful properties of \(\mathbb{R}\), and it essentially states that the set of natural numbers \(\mathbb{N}\) is not bounded above in \(\mathbb{R}\).
More precisley, the Archimedean Property says two things:
For any \(x \in \mathbb{R}\) we can always find a natural number \(n \in \mathbb{N}\) such that \[ n > x \,. \]
For any \(x \in \mathbb{R}\) with \(x>0\), we can always find a natural number \(m \in \mathbb{N}\) such that \[ 0< \frac1m < x \,. \]
The situation is depicted in Figure 4.2.

Remark 1
The Archimedean property might sound trivial. However there are examples of ordered fields \(K\) that satisfy:
- \(\mathbb{N}\subseteq K\).
- \(K\) does not have the Archimedean property.
- In particular, \(\mathbb{N}\) is bounded above in \(K\).
Of course such fields \(K\) cannot be complete.
If \(K\) is complete, then \(K\) is essentially \(\mathbb{R}\), and we are going to prove the Archimedean Property holds in \(\mathbb{R}\).
Let us proceed with the precise statement of the Archimedean property in \(\mathbb{R}\).
Theorem 2: Archimedean Property
Let \(x \in \mathbb{R}\) be given. Then:
There exists \(n \in \mathbb{N}\) such that \[ n > x \,. \]
Suppose in addition that \(x>0\). There exists \(n \in \mathbb{N}\) such that \[ \frac1n < x \,. \]
Proof
Claim: \((\alpha-1)\) is not an upper bound for \(\mathbb{N}\).
Proof of Claim. Indeed, we have \[ (\alpha - 1) < \alpha \,. \tag{4.2}\] Therefore \(\alpha-1\) cannot be an upper bound for \(\mathbb{N}\). Indeed, if by contradiction \(\alpha - 1\) was an upper bound for \(\mathbb{N}\), then we would have \[ \alpha \leq (\alpha - 1)\,, \] since \(\alpha\) is the smallest upper bound for \(\mathbb{N}\). This contradicts (4.2). Therefore \(\alpha - 1\) is not an upper bound for \(\mathbb{N}\).
Conclusion. Since \(\alpha - 1\) is not an upper bound for \(\mathbb{N}\), there exists \(n_0 \in \mathbb{N}\) such that \[ \alpha - 1 < n_0 \,. \] The above implies \[ \alpha < n_0 + 1 \,. \] Since \[ (n_0+1) \in \mathbb{N}\,, \] we have obtained a contradiction, given that \(\alpha\) was the supremum of \(\mathbb{N}\). Thus (4.1) is false, meaning that there exists \(n \in \mathbb{N}\) such that \[ n > x \,. \]
Part 2. Suppose \(x \in \mathbb{R}\) with \(x>0\). We can define \[ y:=\frac1x \,. \] By Part 1 there exists \(n \in \mathbb{N}\) such that \[ n > y = \frac{1}{x} \,. \] Using that \(x>0\), we can rearrange the above inequlaity to obtain \[ \frac1n < x \,, \] which is the desired thesis.
There is another formulation of the Archimedean Property which, depending on the situation, might be more useful. This formulation says the following: If \(x,y \in \mathbb{R}\) are such that \[ 0 < x < y \,, \] then there exists \(n \in \mathbb{N}\) such that \[ nx > y \,. \] In other words, if one does \(n\) steps of size \(x\) in the positive numbers direction, then the resulting number \(nx\) will be larger than \(y\). The situation is depicted in Figure 4.2.

Theorem 3: Archimedean Property (Alternative formulation)
Proof
4.2 Nested Interval Property
Another consequence of the axiom of completeness is the Nested Interval Property. This is yet another way of saying the same thing: \(\mathbb{R}\) does not have gaps.
Let us look at a construction. Suppose given some closed intervals \[ I_n := [a_n,b_n] = \{ x \in \mathbb{R}\, \colon \,a_n \leq x \leq b_n \} \,, \] where the end points are ordered in the following way: \[ a_1 \leq a_2 \leq \ldots \leq a_n \leq \dots \leq b_n \leq \ldots b_n \leq b_1 \,, \] as shown in Figure 4.3.
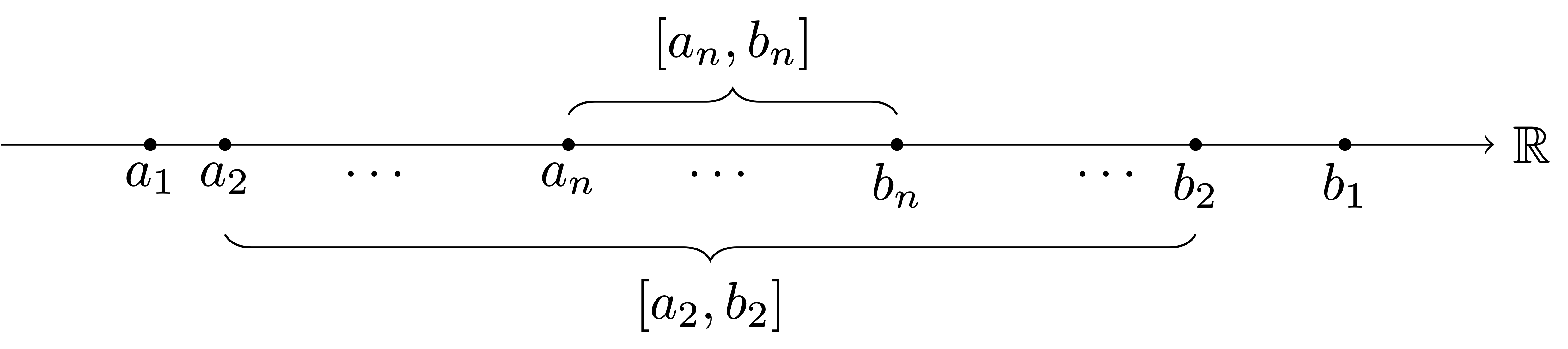
The intervals \(I_n\) are nested, meaning that \[ I_1 \supset I_2 \supset I_3 \supset \ldots I_n \supset \ldots \] For finite intersections we clearly have \[ \bigcap_{n=1}^k I_n = I_k \,, \] that is, intersecting the first \(k\) intervals yields \(I_k\), the smallest interval in the sequence.
Question 4
\[ \bigcap_{n=1}^\infty I_n := \{ x \in \mathbb{R}\, \colon \,x \in I_n \,, \forall \, n \in \mathbb{N}\} \,. \]
What can we say about it? Is it empty? Is it not empty?
The answer is that the infinite intersection is not empty, because \(\mathbb{R}\) was constructed in a way that it does not have gaps.
Theorem 5: Nested Interval Property
Proof
Idea of the Proof: Condition (4.6) is saying that it should hold \[ a_n \leq x \leq b_n \ \,, \quad \forall \, n \in \mathbb{N}\,. \] Since \(a_n\) is increasing and \(b_n\) is decreasing, the point \(x\) is being squeezed between these two sequences. This suggests \(x\) should be the largest (i.e. the supremum) of all \(a_ns\) and smallest (i.e. the infimum) of all the \(b_ns\).
Define the set \[ A:= \{ a_n \, \colon \,n \in \mathbb{N}\} \,. \] The set \(A\) is non-empty and is bounded above by any of the \(b_n\). Therefore there exists \[ x = \sup \ A \,. \] By definition of supremum and definition of the set \(A\), we have \[ a_n \leq x \,, \quad \forall \, n \in \mathbb{N}\,. \] On the other hand, consider an arbitrary number \(b_n\). By construction we have \[ a_i \leq b_n \,, \quad \forall \, i \in \mathbb{N}\,. \] Therefore \(b_n\) is an upper bound for \(A\). Since the supremum is the smallest upper bound, we conclude that \[ x \leq b_n \,. \] The index \(n\) was chosen arbitrarily, and therefore \[ x \leq b_n \,, \quad \forall \, n \in \mathbb{N}\,. \] In total we have \[ a_n \leq x \leq b_n \,, \quad \forall \, n \in \mathbb{N}\,, \] showing that \(x\) satisfies (4.6). Therefore (4.5) holds and the proof is concluded.
Example 6
Solution. Suppose by contradiction that the intersection is non-empty. Then there exists \(x \in \mathbb{N}\) such that \[ x \in I_n \,, \quad \forall \, n \in \mathbb{N}\,. \] By definition of \(I_n\) the above reads \[ 0 < x < \frac1n \,, \quad \forall \, n \in \mathbb{N}\,. \tag{4.8}\] Since \(x>0\), by the Archimedean Property in Theorem 57 Point 2, there exists \(n_0 \in \mathbb{N}\) such that \[ 0 < \frac{1}{n_0} < x \,. \] The above contradicts (4.8). Therefore (4.7) holds.
4.3 Revisiting Sup and inf
We now investigate some of the properties of supremum and infimum in \(\mathbb{R}\). The first property is an alternative characterization of the supremum, which we will often use. A sketch of such characterization is in Figure 4.4 below.
Proposition 7: Characterization of Supremum
Let \(A \subseteq \mathbb{R}\) be a non-empty set. Suppose that \(s \in \mathbb{R}\) is an upper bound for \(A\). They are equivalent:
- \(s = \sup A\)
- For every \(\varepsilon> 0\) there exists \(x \in A\) such that \[ s - \varepsilon< x \,. \]
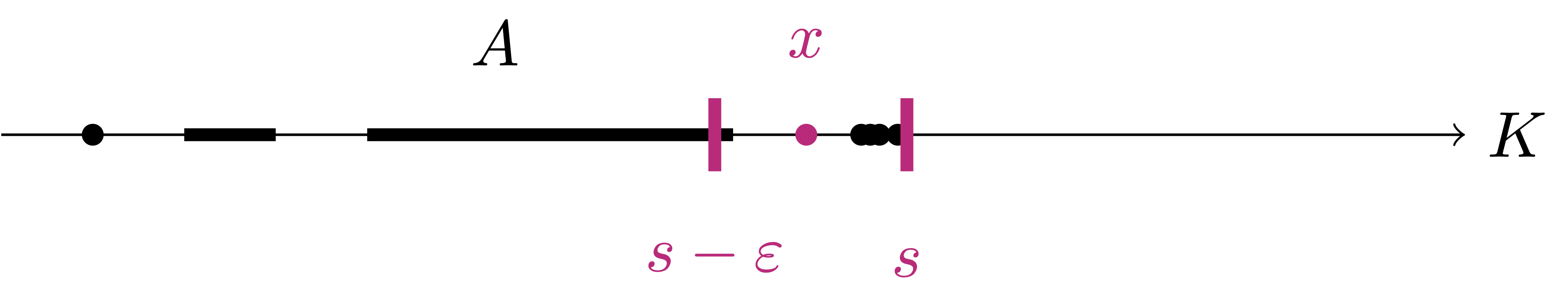
Proof: Proof of Proposition 61
Step 2. Assume that Point 2 in the statement of Proposition 61 holds. By assumption we have that \(s\) is an upper bound for \(A\). Suppose by contradiction that \[ s \neq \sup A \,. \] This is equivalent to the statement \[ s \, \mbox{ is not the smallest upper bound of } \, A. \tag{4.10}\] Hence there exists an upper bound \(b\) of \(A\) such that \[ b < s \,. \] Let \[ \varepsilon:= s - b \,. \] By assumption there exists \(x \in A\) such that \[ s - \varepsilon< x \,. \] Substituting the definition of \(\varepsilon\) we get \[ s - s + b < x \quad \implies \quad b < x \,. \] Since \(b\) is an upper bound for \(A\) and \(x \in A\), the above is a contradiction. Therefore (4.10) is false, and \(s\) is the smallest upper bound of \(A\). Thus \(s = \sup A\).
The analogue of Proposition 61 is as follows. The proof is left as an exercise.
Proposition 8: Characterization of Infimum
Let \(A \subseteq \mathbb{R}\) be a non-empty set. Suppose that \(i \in \mathbb{R}\) is a lower bound for \(A\). They are equivalent:
- \(i = \inf A\)
- For every \(\varepsilon\in \mathbb{R}\), with \(\varepsilon> 0\), there exists \(x \in A\) such that \[ x < i + \varepsilon\,. \]
A sketch of the characterization in Proposition 62 can be found in Figure 4.5 below.
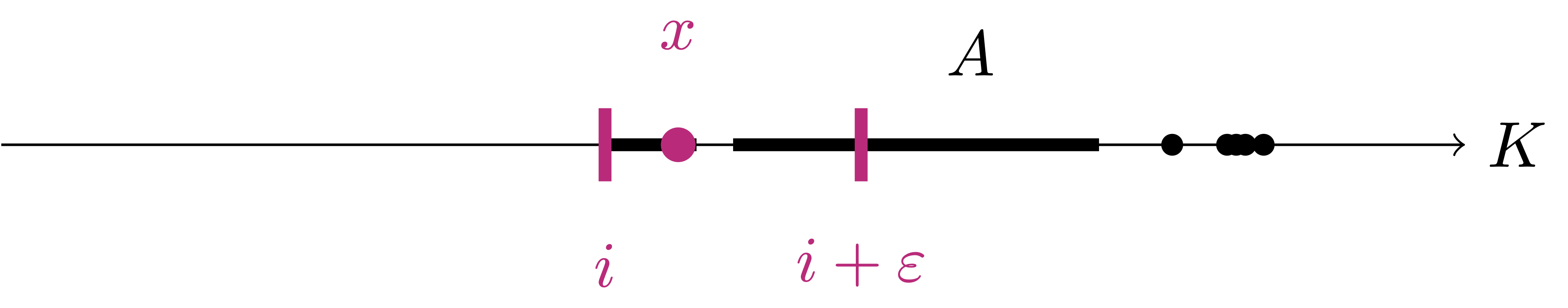
With the above characterizations of supremum and infimum, it will be easier, in some cases, to compute infimum and supremum. We now characterize infimum and supremum of an open interval of \(\mathbb{R}\).
Proposition 9
Let \(a, b \in \mathbb{R}\) with \(a<b\). Let \[ A:= (a,b) = \{ x \in \mathbb{R}\, \colon \,a < x < b \}\,. \]
We have that \[ \inf A = a \,, \quad \sup A = b \,. \]
\(\min A\) and \(\max A\) do not exist.
Proof
By definition of \(A\), we have that \[ a < x \,, \quad \forall \, x \in A \,. \] The above says that \(a\) is a lower bound for \(A\).
Claim. \(a\) is the largest lower bound of \(A\).
Proof of Claim. Let \(L\) be a lower bound for \(A\), that is, \[ L \leq x \,, \quad \forall \, x \in A \,. \] We have to prove that \[ L \leq a \,. \tag{4.11}\] Suppose by contradiction that (4.11) does not hold, namely that \[ a < L \,. \] We want to prove that \(L < b\). To conclude this, first observe that the midpoint between \(a\) and \(b\) belongs to \(A\): \[ \frac{a+b}{2} \in A \,. \]
Indeed, using that \(a<b\), we have \[ \frac{a+b}{2} > \frac{2a}{2} = a \,, \] and \[ \frac{a+b}{2} < \frac{2b}{b} = b \,, \] showing that the midpoint between \(a\) and \(b\) belongs to \(A\).
Since \(L\) is a lower bound for \(A\), and \(\frac{a+b}{2} \in A\), we have \[ L \leq \frac{a+b}{2} < b \,, \tag{4.12}\] where in the second inequality we used that \(a<b\). In particular, we have proven that \(a < L <b\), which means that \(L \in A\).
We now want to find an element of \(A\) which is less than \(L\). A good candidate is the midpoint between \(a\) and \(L\), that is, \[ M := \frac{a + L}{2} \,. \] Since \(a < L <b\), we have that \[ M \in A \,. \]
Indeed, using that \(a<L\), we have \[ a = \frac{2a}{2} < \frac{a+L}{2} = M \leq \frac{a+b}{2} \,. \] Using that \(L<b\), we have \[ M = \frac{a+L}{2} \leq \frac{a+b}{2} < b \,. \] Thus \(a < M < b\), showing that \(M \in A\).
Moreover \[ M < L \,. \]
This is because \(a<L\), and therefore \[ M = \frac{a + L}{2} < \frac{2L}{2} = L \,. \]
This is a contradiction, since \(L\) is a lower bound for \(A\) and \(M \in A\). Therefore (4.11) holds, showing that \(a\) is the largest lower bound of \(A\). We conclude that \(a = \inf A\).
Part 2. Suppose by contradiction that \(\min A\) exists. We have shown that if the minimum of a set exists, then it must be \[ \min A = \inf A \,. \] Since \[ \inf A = a\,, \] by Proposition 63, we would obtain that \[ \min A = a \,. \] As \(\min A \in A\) by definition, we infer \(a \in A\). This is contradiction. Then \(\min A\) does not exist.
The proof that \(\max A\) does not exist is similar, and is left as an exercise.
We can also consider intervals for which one or both of the sides are closed.
Corollary 10
The proof is very simple, and is left as an exercise. Let us now compute supremum and infimum of a set which is not an interval.
Proposition 11
Proof
Part 2. We have \[ \frac1n > 0 \,, \quad \forall \, n \in \mathbb{N}\,, \] showing that \(0\) is a lower bound for \(A\). Suppose by contradiction that \(0\) is not the infimum. Therefore \(0\) is not the largest lower bound. Then there exists \(\varepsilon\in \mathbb{R}\) such that:
\(\varepsilon\) is a lower bound for \(A\), that is, \[ \varepsilon\leq \frac1n \,, \quad \forall \, n \in \mathbb{N}\,, \tag{4.13}\]
\(\varepsilon\) is larger than \(0\): \[ 0 < \varepsilon\,. \]
As \(\varepsilon>0\), by the Archimedean Property there exists \(n_0 \in \mathbb{N}\) such that \[ 0 < \frac{1}{n_0} < \varepsilon\,. \] This contradicts (4.13). Thus \(0\) is the largest lower bound of \(A\), that is, \(0 = \inf A\).
Part 3. We have that \(\min A\) does not exist. Indeed suppose by contradiction that \(\min A\) exists. Then \[ \min A = \inf A \,. \] As \(\inf A = 0\) by Part 2, we conclude \(\min A = 0\). As \(\min A \in A\), we obtain \(0 \in A\), which is a contradiction.
4.4 Existence of \(k\)-th Roots
We have started our discussion in Chapter 1 by proving that \[ \sqrt{2} \notin \mathbb{Q}\,. \tag{4.14}\] We have shown that (4.14) implies that the set \[ A := \{ q \in \mathbb{Q}\, \colon \,q^2 < 2 \} \] does not have a supremum in \(\mathbb{Q}\). We then introduced the Real Numbers \(\mathbb{R}\) so that each non-empty and bounded above set would have a supremum. As the set \(A\) is non-empty and bounded above, there exists \(\alpha \in \mathbb{R}\) such that \[ \alpha = \sup A \,. \] We are going to prove that \[ \alpha^2 = 2 \,, \] which means that \(\alpha\) is the square root of \(2\).
More in general, we can prove existence of \(k\)-th roots: Let \(x \in \mathbb{R}\) with \(x \geq 0\) and \(k \in \mathbb{N}\). Define the set \[ A := \{ t \in \mathbb{R}\, \colon \,t^k < x \} \] We will see that \(A\) is non-empty and bounded above. By the axiom of completeness there exists \(\alpha \in \mathbb{R}\) such that \[ \alpha = \sup A \] In the following Theorem we will prove that \[ \alpha^k = x \,, \] meaning that \(\alpha\) is the \(k\)-th root of \(x\).
Theorem 12: Existence of \(k\)-th roots
The proof of Theorem 12 rests on similar ideas to the ones used to prove that \(\mathbb{Q}\) does not have the cut property.
Proof: Proof of Theorem 12
Suppose \(\alpha_1,\alpha_2 \in \mathbb{R}\) are such that \[ \alpha_1^k = \alpha_2^k = x \,. \] If \(\alpha_1 \neq \alpha_2\), then \[ \alpha_1^k \neq \alpha_2^k \,, \] obtaining a contradiction. Therefore \(\alpha_1 = \alpha_2\).
Part 2: Existence.
Let \(x \in \mathbb{R}\) with \(x \geq 0\). If \(x = 0\) there is nothing to prove, as \[ 0^k = 0 \,, \] so that \(\alpha = 0\). Therefore we can assume \(x>0\). Define the subset of \(\mathbb{R}\) \[ A := \{ t \in \mathbb{R}\, \colon \,t^k < x \} \,. \] Clearly \(A\) is non-empty and bounded above.
An upper bound is given, for example, by \(b := x + 1\). Indeed, since we are assuming \(x \geq 0\), then \(x+1 \geq 1\). In particular we have \[ (x+1)^k \geq x + 1 \,. \] Let \(t \in A\). Then \[ t^k < x < x + 1 < (x+1)^k , \] showing that \(t< x+1\).
By the Axiom of Completeness of \(\mathbb{R}\), there exists \(\alpha \in \mathbb{R}\) such that \[ \alpha = \sup A \,. \] We claim that \[ \alpha^k = x \,. \tag{4.15}\] Suppose by contradiction that (4.15) does not hold. We will need the formula: For all \(a,b \in \mathbb{R}\) it holds \[ a^k-b^k = (a - b)( a^{k-1} + a^{k-2} b + a^{k-3}b^k + \ldots + a b^{k-2} + b^{k-1} ) \,. \tag{4.16}\] Formula (4.16) can be easily proven by induction on \(k\). Since we are assuming that (4.15) does not hold, we have two cases:
\(\alpha^k < x\): We know that \(\alpha\) is the supremum of \(A\). We would like to violate this, by finding a number \(L\) which is larger than \(\alpha\), but still belongs to \(A\). This means \(L\) has to satisfy \[ \alpha < L \,, \quad L^k < x \,. \] We look for \(L\) of the form \[ L_n := \alpha + \frac{1}{n} \] for \(n \in \mathbb{N}\) to be chosen later. Clearly \[ \alpha < L_n \,, \tag{4.17}\] for all \(n \in \mathbb{N}\). We now search for \(n_0 \in \mathbb{N}\) such that \[ L_{n_0}^k < x \,. \] Using formula (4.16) with \(a = \alpha\) and \(b = L_{n_0}\) we obtain \[ L_{n_0}^k - \alpha^k = \frac{1}{n_0} \left( L_{n_0}^{k-1} + L_{n_0}^{k-2} \alpha + \ldots + L_{n_0}\alpha^{k-2} + \alpha^{k-1} \right) \,. \tag{4.18}\] Now notice that (4.17) implies \[ \alpha^j < L_{n_0}^j \] for all \(j \in \mathbb{N}\). Using this estimate on all the terms \(\alpha^j\) appearing in the RHS of (4.18) we obtain \[\begin{align*} L_{n_0}^k - \alpha^k & = \frac{1}{n_0} \left( L_{n_0}^{k-1} + L_{n_0}^{k-2} \alpha + \ldots + L_{n_0}\alpha^{k-2} + \alpha^{k-1} \right) \\ & < \frac{1}{n_0} \left( L_{n_0}^{k-1} + L_{n_0}^{k-2} L_{n_0} + \ldots + L_{n_0} L_{n_0}^{k-2} + L_{n_0}^{k-1} \right) \\ & = \frac{k}{n_0} \, L_{n_0}^{k-1} \end{align*}\] Rearranging the above we get \[ L_{n_0}^k < \frac{k}{n_0} \, L_{n_0}^{k-1} + \alpha^k \,. \tag{4.19}\] Now note that \[ L_{n_0} = \alpha + \frac{1}{n_0} < \alpha + 1 \,. \] Therefore \[ L_{n_0}^{k-1} < (\alpha + 1)^{k-1} \,, \] and from (4.19) we obtain \[ L_{n_0}^k < \frac{k}{n_0} \, (\alpha + 1)^{k-1} + \alpha^k \,. \] We wanted to find \(n_0 \in \mathbb{N}\) so that \(L_{n_0}^k < x\). Therefore we impose \[ \frac{k}{n_0} \, (\alpha + 1)^{k-1} + \alpha^k < x \,, \] and find that the above is satisfied for \[ n_0 > \frac{ k (\alpha + 1)^{k-1} }{ x - \alpha^k } \,. \tag{4.20}\] Notice that the RHS in (4.20) is a positive real number, since \(\alpha^k < x\) by assumption. Therefore, by the Archimedean Property of Theorem 57 Point 1, there exists \(n_0 \in \mathbb{N}\) satisfying (4.20).
We have therefore shown the existence of \(n_0 \in \mathbb{N}\) such that \[ \alpha < L_{n_0} \,, \quad L_{n_0}^k < x \,. \] The above says that \(L_{n_0} \in A\) and that \[ L_{n_0} > \alpha = \sup A \,, \] which is a contradiction, as \(\sup A\) is an upper bound for \(A\).\(\alpha^k > x\): We know that \(\alpha\) is the supremum of \(A\). We would like to find a contradiction, by finding an upper bound \(L\) for \(A\) which is smaller than \(\alpha\). This means \(L\) has to satisfy \[ L < \alpha \,, \quad L^k > x \,. \]
Such \(L\) is an upper bound for \(A\): If \(t \in A\) then \[ t^k < x < L^k \quad \implies \quad t < L \,. \]
We therefore look for \(L\) of the form \[ L_n := \alpha - \frac{1}{n} \] for \(n \in \mathbb{N}\) to be chosen later. In this way \[ L_n < \alpha \,, \tag{4.21}\] for all \(n \in \mathbb{N}\). We now search for \(n_0 \in \mathbb{N}\) such that \[ L_{n_0}^k > x \,. \] Using formula (4.16) with \(a = L_{n_0}\) and \(b = \alpha\) we obtain \[ \alpha^k - L_{n_0}^k = \frac{1}{n_0} \left( \alpha^{k-1} + \alpha^{k-2} L_{n_0} + \ldots + \alpha L_{n_0}^{k-2} + L_{n_0}^{k-1} \right) \,. \tag{4.22}\] Now notice that (4.21) implies \[ L_{n_0}^j < \alpha^j \] for all \(j \in \mathbb{N}\). Using this estimate on all the terms \(L_{n_0}^j\) appearing in the RHS of (4.22) we obtain \[\begin{align*} \alpha^k - L_{n_0}^k & = \frac{1}{n_0} \left( \alpha^{k-1} + \alpha^{k-2} L_{n_0} + \ldots + \alpha L_{n_0}^{k-2} + L_{n_0}^{k-1} \right) \\ & < \frac{1}{n_0} \left( \alpha^{k-1} + \alpha^{k-2} \alpha + \ldots + \alpha \alpha^{k-2} + \alpha^{k-1} \right) \\ & = \frac{k}{n_0} \, \alpha^{k-1} \end{align*}\] Rearranging the above we get \[ L_{n_0}^k > \alpha^k - \frac{k}{n_0} \, \alpha^{k-1} \,. \] We wanted to find \(n_0 \in \mathbb{N}\) so that \(L_{n_0}^k > x\). Therefore we impose \[ \alpha^k - \frac{k}{n_0} \, \alpha^{k-1} > x \,, \] and find that the above is satisfied for \[ n_0 > \frac{ k \alpha^{k-1} }{ \alpha^k - x} \,. \tag{4.23}\] Notice that the RHS in (4.23) is a positive real number, since \(\alpha^k > x\) by assumption. Therefore, by the Archimedean Property of Theorem 57 Point 1, there exists \(n_0 \in \mathbb{N}\) satisfying (4.23).
We have therefore shown the existence of \(n_0 \in \mathbb{N}\) such that \[ L_{n_0} < \alpha \,, \quad L_{n_0}^k > x \,. \] Condition \(L_{n_0}^k > x\) says that \(L_{n_0}\) is an upper bound for \(A\). At the same time it holds \[ L_{n_0} < \alpha = \sup A \,, \] which is a contradiction, as \(\sup A\) is the smallest upper bound for \(A\).
Therefore, both cases \(\alpha^k > x\) and \(\alpha^k < x\) lead to a contradiction. Hence \(\alpha^k =x\), concluding.
Definition 13: \(k\)-th root of a number
4.5 Density of \(\mathbb{Q}\) in \(\mathbb{R}\)
A set \(S\) is dense in \(\mathbb{R}\) if the elements of \(S\) are arbitrarily close to the elements of \(\mathbb{R}\).
Definition 14: Dense set
In other words, the above definition is saying that \(S\) and \(\mathbb{R}\) are tightly knitted together. An equivalent definition of dense set is given below.
Remark 15
Let \(S \subseteq \mathbb{R}\). They are equivalent:
- \(S\) is dense in \(\mathbb{R}\).
- For every pair of numbers \(x,y \in \mathbb{R}\) with \(x<y\), there exists \(s \in S\) such that \[ x < s < y \,. \]
We now prove that \(\mathbb{Q}\) is dense in \(\mathbb{R}\).
Theorem 16: Density of \(\mathbb{Q}\) in \(\mathbb{R}\)

Proof
To this end, note that \(y - x >0\) by assumption. By the Archimedean Property in Theorem 57 Point 2, there exists \(n \in \mathbb{N}\) such that \[ \frac{1}{n} < y - x \,. \tag{4.26}\] Now, we would like to find \(m \in \mathbb{Z}\) such that \[ x < \frac{m}{n} \,. \] However \(m\) cannot be too large, because we also want to have \[ \frac{m}{n} < y \,. \] The right thing to do, is to take \(m \in \mathbb{Z}\) such that \[ \frac{m-1}{n} \leq x < \frac{m}{n} \,. \tag{4.27}\]
Why does such \(m\) exist? The inequality in (4.27) is equivalent to \[ m-1 \leq nx < m \,. \] As \(nx>0\), by Archimedean Property in Theorem 57 Point 1, there exists \(m \in \mathbb{Z}\) such that \[ nx < m \] We can then choose \(m'\) to be the smallest element in \(\mathbb{Z}\) such that \[ nx < m' \,. \tag{4.28}\] For such \(m'\), we have that \[ m'-1 \leq nx < m' \,. \] Indeed, if by contradiction \[ m' - 1 > nx \,, \] then \(m'-1\) would be another integer such that (4.28) holds. Since \(m'-1<m'\), this contradicts the minimality of \(m'\).
The second inequality in (4.27) implies \[ x < \frac{m}{n} \,, \] which is the first inequality in (4.25). Now note that (4.26) is equivalent to \[ x < y - \frac{1}{n} \,. \] We can use the above, and the first inequality in (4.27) to estimate \[\begin{align*} m & \leq 1 + nx \\ & < 1 + n \left( y - \frac{1}{n} \right ) \\ & = ny \,, \end{align*}\] which yields \[ \frac{m}{n} < y \,. \] Therefore the second inequality in (4.25) is proven, concluding the proof.
We have constructed the real numbers \(\mathbb{R}\) so that they would fill the gaps of \(\mathbb{Q}\). Formally, these gaps are the numbers in \(\mathbb{R}\smallsetminus \mathbb{Q}\). Let us give a name to this set.
Definition 17: Irrational numbers
Question 18
The answer is quite surprising, and is a corollary of the density result of Theorem 16: The irrational numbers are dense in \(\mathbb{R}\).
Corollary 19
Proof
4.6 Cardinality
We have proven that the sets or rational numbers \(\mathbb{Q}\) and irrational numbers \(\mathcal{I}\) are both dense in \(\mathbb{R}\), with \[ \mathbb{R}= \mathbb{Q}\cup \mathcal{I} \,. \] From this result we might think that \(\mathbb{R}\) is obtained by mixing \(\mathbb{Q}\) and \(\mathcal{I}\) in equal proportions. This is however false. We will see that \(\mathbb{R}\) has much more elements than \(\mathbb{Q}\). Therefore also the set of irrational numbers \(\mathcal{I}\) is much larger than \(\mathbb{Q}\).
To make the above discussion precise, we need to introduce the size of a set. For this, we need the concept of bijective function.
Definition 20: Bijective function
Let \(X,Y\) be sets and \(f \colon X \to Y\) be a function. We say that:
\(f\) is injective if it holds: \[ f(x)=f(y) \quad \implies \quad x = y \,. \]
\(f\) is surjective if it holds: \[ \forall \, y \in Y \,, \,\, \exists \, x \in X \, \text{ s.t. } \, f(x) = y \,. \]
\(f\) is bijective if it is both injective and surjective.
In other words: A function \(f \colon X \to Y\) is:
- Injective if any two different elements in \(X\) are mapped into two different elements in \(Y\).
- Surjective if every element in \(Y\) has at least one element in \(X\) associated via \(f\).
- Bijective if to each element in \(X\) we associate one and only one element in \(Y\) via \(f\).
Example 21: Injectivity
Consider the sets \[ X = \{ 1, 2, 3 \} \,, \quad Y = \{ a,b,c,d,e\} \,. \]
The function \(f \colon X \to Y\) defined by \[ f(1)=c \,, \quad f(2) = a \,, \quad f(3) = e \,, \] is injective.
The function \(g \colon X \to Y\) defined by \[ g(1)=c \,, \quad g(2) = a \,, \quad g(3) = c \,, \] is not injective, since \[ g(1) = g(3) = c \,, \quad 1 \neq 3 \,. \]
The function \(h \colon \mathbb{R}\to \mathbb{R}\) defined by \[ h(x) = x^2 \] is not injective, since \[ h(1) = h(-1) = 1 \,, \quad 1 \neq - 1 \,. \]
The function \(l \colon \mathbb{R}\to \mathbb{R}\) defined by \[ l(x) = 2x \] is injective, since \[ l(x) = l(y) \quad \implies \quad 2x = 2y \quad \implies \quad x = y \,. \]
Example 22: Surjectivity
Consider the sets \[ X = \{ 1, 2, 3 ,4\} \,, \quad Y = \{ a,b,c\} \,. \]
The function \(f \colon X \to Y\) defined by \[ f(1)=c \,, \quad f(2) = a \,, \quad f(3) = a \,, \quad f(4) = b \,, \] is surjective.
The function \(g \colon X \to Y\) defined by \[ g(1)=a \,, \quad g(2) = a \,, \quad g(3) = c \,, \quad g(4) = a \,, \] is not surjective, since there is no element \(x \in X\) such that \[ g(x) = b \,. \]
The function \(h \colon \mathbb{R}\to \mathbb{R}\) defined by \[ h(x) = x^2 \] is not surjective, since there is no \(x \in \mathbb{R}\) such that \[ h(x) = x^2 = -1 \,. \]
The function \(l \colon \mathbb{R}\to [0 , \infty)\) defined by \[ l(x) = x^2 \] is surjective, since for every \(y \geq 0\) there exists \(x \in \mathbb{R}\) such that \[ l(x)= x^2 = y\,. \] This is true by Theorem 12.
Example 23: Bijectivity
Let \(X = \{ 1, 2, 3 \}, Y = \{ a,b,c\}\). The function \(f \colon X \to Y\) defined by \[ f(1)=c \,, \quad f(2) = a \,, \quad f(3) = b \,, \] is bijective, since it is both injective and surjective.
Let \(X = \{ 1, 2, 3 \}, Y = \{ a,b\}\). The function \(g \colon X \to Y\) defined by \[ g(1)=a \,, \quad g(2) = b \,, \quad g(3) = b \,, \] is not bijective, since it is not injective: we have \[ g(2) = g(3) = b \, \quad 2 \neq 3 \,. \]
Let \(X = \{ 1, 2 \}, Y = \{ a,b,c\}\). The function \(h \colon \mathbb{R}\to \mathbb{R}\) defined by \[ h(1) = a \,, \quad h(2) = c \,, \] is not bijective, since it is not surjective: there is no \(x \in X\) such that \[ h(x) = b \,. \]
Let \(X = \{ 1, 2 , 3\}, Y = \{ a,b,c\}\). The function \(l \colon \mathbb{R}\to [0 , \infty)\) defined by \[ l(1) = a \,, \quad l(2) = a \,, \quad l(3) = b \,, \] is not bijective, as it is neither injective nor surjective.
Definition 24: Composition of functions
Definition 25: Identity map
Definition 26: Invertibility
Let \(X,Y\) be sets and \(f \colon X \to Y\). We say that:
A function \(g \colon Y \to X\) is the inverse of \(f\) if \[ g \circ f = \operatorname{id}_X \,, \quad f \circ g = \operatorname{id}_Y \,. \]
\(f\) is invertible if it admits an inverse \(g\).
Proposition 27
Let \(X,Y\) be sets and \(f \colon X \to Y\).
If \(f\) is invertible, the inverse is unique. We denote it by \[ g:=f^{-1} \,. \]
They are equivalent:
- \(f\) is invertible.
- \(f\) is bijective.
We are ready to define the size of a set.
Definition 28: Cardinality, Finite, Countable, Uncountable
Let \(X\) be a set. The cardinality of \(X\) is the number of elements in \(X\). We denote the cardinality of \(X\) by \[ |X| := \# \, \mbox{ of elements in } \, X \,. \] Further, we say that:
\(X\) is finite if there exists a natural number \(n \in \mathbb{N}\) and a bijection \[ f \colon \{1,2,\ldots, n \} \to X \,. \] In particular \[ |X| = n \,. \]
\(X\) is countable if there exists a bijection \[ f \colon \mathbb{N}\to X \,. \] In this case we denote the cardinality of \(X\) by \[ |X| = |\mathbb{N}| \,. \]
\(X\) is uncountable if \(X\) is neither finite, nor countable.
In other words:
\(X\) is finite if it can be listed as \[ X = \{ x_1 , \ldots, x_n \} \,, \quad x_i := f(i) \] for some \(n \in \mathbb{N}\).
\(X\) is countable if it can be listed as \[ X = \{ x_n \, \colon \,n \in \mathbb{N}\} \,, \quad x_n := f(n) \]
\(X\) is uncountable if it \(X\) cannot be listed.
Remark 29
Question 30
The answer is no, as shown in the next proposition.
Proposition 31
Proof
We define \[ g(1) := f(n_1) = x_{n_1} \,. \] Now, we want to find the second element of \(A\) in the list of elements of \(X\). We need to make sure that we do not pick \(x_{n_1}\) again. Therefore, we define the set of indices of elemets in \(A\) wich are not \(x_{n_1}\): \[\begin{align*} I_2 & := \{ n \in \mathbb{N}\, \colon \, n > n_1 \,, f(n) \in A \} \\ & = \{ n \in \mathbb{N}\, \colon \,n > n_1 \,, x_n \in A \} \,. \end{align*}\] This way \(I_2\) does not contain \(n_1\), but only successive indices. Note that \(I_2\) is non-empty, since \(f\) is surjective and \(A\) is an infinite subset of \(X\). Therefore it is well defined \[ n_2 := \min I_2 \,. \] Notice that by construction \[ n_1 < n_2 \,, \quad x_{n_2} \in A \,. \] Set \[ g(2):=f(n_2) \,. \] Iterating this procedure, we define \[\begin{align*} I_k & := \{ n \in \mathbb{N}\, \colon \, n > n_{k-1} \,, f(n) \in A \} \\ & = \{ n \in \mathbb{N}\, \colon \,n > n_{k-1} \,, x_n \in A \} \,. \end{align*}\] and set \[ n_k = \min I_k \,, \quad g(k) := f(n_k) \,. \] Note that, by construction, we have \[ n_k > n_{k-1} \,, \quad x_{n_k} \in A \,, \quad \forall \, k \in \mathbb{N}\,. \] In this way we have defined a function \[ g \colon \mathbb{N}\to A \,. \]
We have:
\(g\) is injective: Suppose \(g(k) = g(s)\). Then \(f(n_k) = f(n_s)\). From injectivity of \(f\) we infer \(n_k = n_s\). Since \(n_{k}> n_{k-1}\) for all \(k\), from the condition \(n_k = n_s\) we conclude that \(k = s\). This shows \(g\) is injective.
\(g\) is surjective: If \(x \in A\), by surjectivity of \(f\) there exists \(\widetilde{n} \in \mathbb{N}\) such that \(f(\widetilde{n})=x\). Therefore \[ \widetilde{n} \in \{ n \in \mathbb{N}\, \text{ s.t. } \, f(n) \in A \} = I_1 \,. \] Hence, by construction, there is an index \(k \in \mathbb{N}\) such that \(n_k= \widetilde{n}\). Thus \(g(k) = f(n_k) = x\), showing that \(g\) is surjective.
Hence \(g\) is bijective, showing that \(A\) is countable.
Example 32
Solution. Set \(Y=\{ 1,2,3\}\). The function \(f \colon X \to Y\) defined by \[ f(1)=a \,, \quad f(2) = b \,, \quad f(3) = c \,, \] is bijective. Therefore \(X\) is finite, with \(|X| = 3\).
Example 33
Solution. The function \(f \colon X \to \mathbb{N}\) defined by \[ f(n):=n \,, \] is bijective. Therefore \(X = \mathbb{N}\) is countable.
Example 34
Solution. Define the map \(f \colon \mathbb{N}\to X\) by \[ f(n):= 2n \,. \] We have that:
\(f\) is injective, because \[ f(m)=f(k) \, \implies \, 2m=2k \, \quad \, m=k \,. \]
\(f\) is surjective: Suppose that \(m \in X\). By definition of \(X\), there exists \(n \in \mathbb{N}\) such that \(m = 2n\). Therefore, \(f(n) = m\).
We have shown that \(f\) is bijective. Thus, \(X\) is countable.
Example 35
Solution. Define \(f \colon \mathbb{N}\to \mathbb{Z}\) by \[ f(n):= \begin{cases} \dfrac{n}{2} & \,\, \mbox{ if } \, n \, \mbox{ even } \\ -\dfrac{n+1}{2} & \,\, \mbox{ if } \, n \, \mbox{ odd } \end{cases} \] For example \[\begin{align*} f(0) & = 0 \,, \quad f(1) = -1 \,, \quad f(2) = 1 \,, \quad f(3) = -2 \,, \\ f(4) & = 2 \,, \quad f(5) = -3 \,, \quad f(6) = 3 \,, \quad f(7) = -4 \,. \end{align*}\] We have:
\(f\) is injective: Indeed, suppose that \(m \neq n\). If \(n\) and \(m\) are both even or both odd we have, respectively \[\begin{align*} f(m) = \frac{m}{2} & \neq \frac{n}{2} = f(n) \\ f(m) = -\frac{m+1}{2} & \neq - \frac{n+1}{2} = f(n) \,. \end{align*}\] If instead \(m\) is even and \(n\) is odd, we get \[ f(m) = \frac{m}{2} \neq - \frac{n+1}{2} = f(n) \,, \] since the LHS is positive and the RHS is negative. The case when \(m\) is odd and \(n\) even is similar.
\(f\) is surjective: Let \(z \in \mathbb{Z}\). If \(z \geq 0\), then \(m:=2z\) belongs to \(\mathbb{N}\), is even, and \[ f(m) = f(2z) = z \,. \] If instead \(z < 0\), then \(m := -2z -1\) belongs to \(\mathbb{N}\), is odd, and \[ f(m) = f(-2z-1) = z \,. \]
Therefore \(f\) is bijective, showing that \(\mathbb{Z}\) is countable.
We have seen that the sets \(\mathbb{N}\) and \(\mathbb{Z}\) are countable. What about \(\mathbb{Q}\)? To study this case, we need the following result.
Proposition 36
Proof
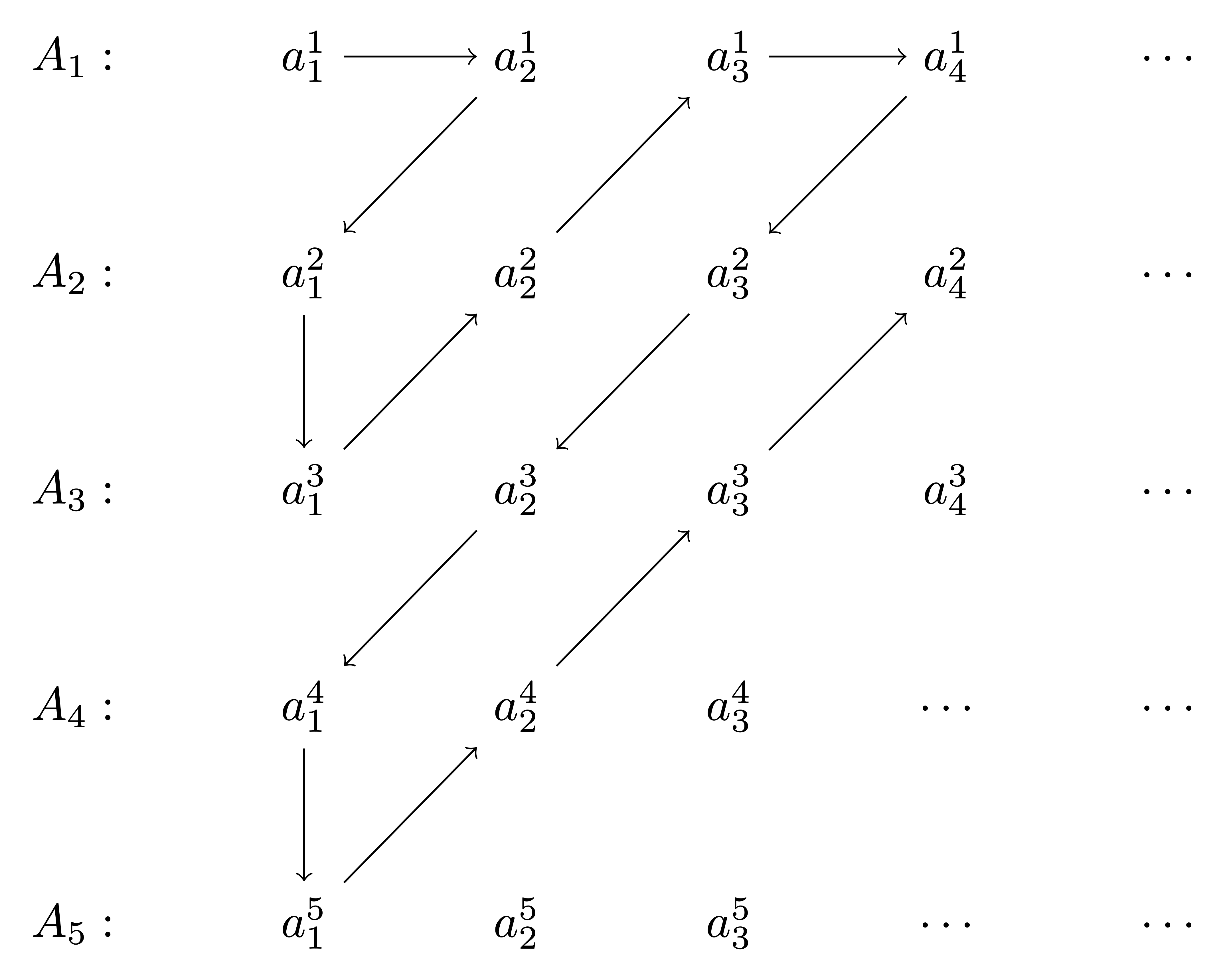
Theorem 37: \(\mathbb{Q}\) is countable
Proof
We have proven that the sets \[ \mathbb{N}\,, \quad \mathbb{Z}\,, \quad \mathbb{Q}\,, \] are all countable. What about \(\mathbb{R}\)?
Theorem 38: \(\mathbb{R}\) is uncountable
Proof
If \(x_2 \in I_1\), then we can find a closed interval \(I_2\) such that \[ x_2 \notin I_2 \,, \quad I_2 \subseteq I_1 \tag{4.30}\]
If \(x_2 \notin I_1\), we define the closed interval \(I_2 := I_1\). By construction, (4.30) is satisfied.
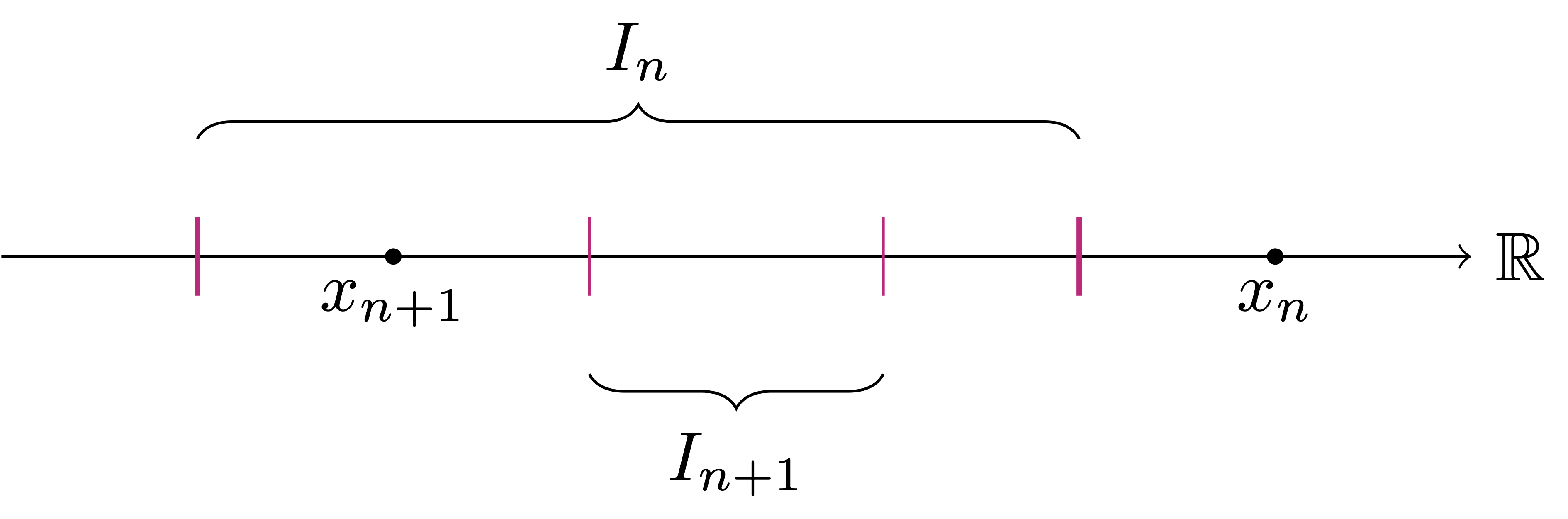
To summarize, we have found closed intervals \(I_1\) and \(I_2\) such that \[ x_1 \notin I_1 \,, \quad x_2 \notin I_2 \,, \quad I_2 \subseteq I_1 \,. \] We can iterate this procedure, and construct a sequence of closed nested intervals \(I_n\) such that \[ I_{n+1} \subseteq I_n \,, \quad x_n \notin I_n \,, \] for all \(n \in \mathbb{N}\), see Figure 4.8. Since \(x_k \notin I_k\), we conclude that \[ x_k \notin \bigcap_{n =1}^\infty \, I_n \,, \quad \forall \, k \in \mathbb{N}\,. \] As the points \(x_k\) are all the elements of \(\mathbb{R}\), we conclude that \[ \bigcap_{n =1}^\infty \, I_n = \emptyset \,. \] However, since each \(I_n\) is closed, the Nested Interval Property of Theorem 59 implies that \[ \bigcap_{n =1}^\infty \, I_n \neq \emptyset \,, \] yielding a contradiction. Therefore \(\mathbb{R}\) is uncountable.
As a corollary we obtain that also the irrational numbers are uncountable.