4 Complex Numbers
Definition 1: Complex Numbers
The set of complex numbers \(\mathbb{C}\) is defined as
\[ \mathbb{C}:= \mathbb{R}+ i \mathbb{R}:= \{x + i y \, \colon \,x, y \in \mathbb{R}\} \,. \] For a complex number \[ z = x + i y \in \mathbb{C} \] we say that
- \(x\) is the real part of \(z\), and denote it by \[ x = \operatorname{Re}(z) \]
- \(y\) is the imaginary part of \(z\), and denote it by \[ y = \operatorname{Im}(z) \]
We say that
- If \(\operatorname{Re}z = 0\) then \(z\) is a purely imaginary number.
- If \(\operatorname{Im}z = 0\) then \(z\) is a real number.
Definition 2: Addition and multiplication in \(\mathbb{C}\)
Let \(z_1,z_2 \in \mathbb{C}\), so that \[ z_1 = x_1 + i y_1 \,\,, \quad z_2 = x_2 + i y_2 \,\, , \] for some \(x_1,x_2,y_1,y_2 \in \mathbb{R}\):
The sum of \(z_1\) and \(z_2\) is \[ z_1 + z_2 :=\left(x_{1}+x_{2}\right) + i \left(y_{1}+y_{2}\right) \,. \]
The multiplication of \(z_1\) and \(z_2\) is \[\begin{align*} z_1 \cdot z_2 := \left(x_{1} \cdot x_{2} - y_{1} \cdot y_{2}\right) + i \left(x_{1} \cdot y_{2} + x_{2} \cdot y_{1} \right) \,, \end{align*}\]
Example 3
Solution. Using the definition we compute \[\begin{align*} z \cdot w & = (-2+3 i) \cdot (1 - i) \\ & = (-2-(-3))+(2+3) i \\ & = 1 + 5 i \, . \end{align*}\] Alternatively, we can proceed formally: We just need to recall that \(i^2\) has to be replaced with \(-1\): \[\begin{align*} z \cdot w & = (-2+3 i) \cdot (1 - i) \\ & = - 2 + 2i + 3i - 3 i^2 \\ & = (-2 + 3 ) + ( 2 + 3 ) i \\ & = 1 + 5 i \, . \end{align*}\]
Proposition 4: Additive inverse in \(\mathbb{C}\)
Proposition 5: Multiplicative inverse in \(\mathbb{C}\)
Proof
Example 6
Solution. By the formula in Propostion 5 we immediately get \[ z^{-1} = \frac{3}{3^{2}+2^{2}} + \, \frac{-2}{3^{2}+2^{2}} \, i = \frac{3}{13}-\frac{2}{13} \, i \,. \] Alternatively, we can proceed formally: \[\begin{align*} (3+2 i)^{-1} & = \frac{1}{3+2 i} \\ & = \frac{1}{3+2 i} \, \frac{3-2 i}{3-2 i} \\ & = \frac{3-2 i}{3^2+2^2} \\ & = \frac{3}{13}-\frac{2}{13} i \,, \end{align*}\] and obtain the same result.
Theorem 7
Example 8
Question. Let \(w=1+i\) and \(z=3-i\). Compute \(\frac{w}{z}\).
Solution. We compute \(w/z\) using the two options we have:
Using the formula for the inverse from Proposition 5 we compute \[\begin{align*} z^{-1} & = \frac{x}{x^{2}+y^{2}} + i \, \frac{-y}{x^{2}+y^{2}} \\ & = \frac{3}{3^2 + 1^2} - i \, \frac{-1}{3^2 + 1^2} \\ & = \frac{3}{10} + \frac{1}{10} \, i \end{align*}\] and therefore \[\begin{align*} \frac{w}{z} & = w \cdot z^{-1} \\ & = (1 + i) \, \left( \frac{3}{10} + \frac{1}{10} \, i \right) \\ & = \left(\frac{3}{10}-\frac{1}{10}\right)+\left(\frac{1}{10}+\frac{3}{10}\right) i \\ & = \frac{2}{10}+\frac{4}{10} i \\ & = \frac{1}{5}+\frac{2}{5} i \end{align*}\]
We proceed formally, using the multiplication by \(1\) trick. We have \[\begin{align*} \frac{w}{z} & = \frac{1+i}{3-i} \\ & = \frac{1+i}{3-i} \frac{3+i}{3+i} \\ & = \frac{3-1+(3+1) i}{3^2+1^2} \\ & =\frac{2}{10}+\frac{4}{10} i \\ & = \frac{1}{5}+\frac{2}{5} i \end{align*}\]
Definition 9: Complex conjugate
\[ \bar{z}=x- i y \, . \]
Theorem 10
For all \(z_1, z_2 \in \mathbb{C}\) it holds:
\(\overline{z_1 + z_2 }=\overline{z_1}+\overline{z_2}\)
\(\overline{z_1 \cdot z_2}=\overline{z_1} \cdot \overline{z_2}\)
4.1 The complex plane
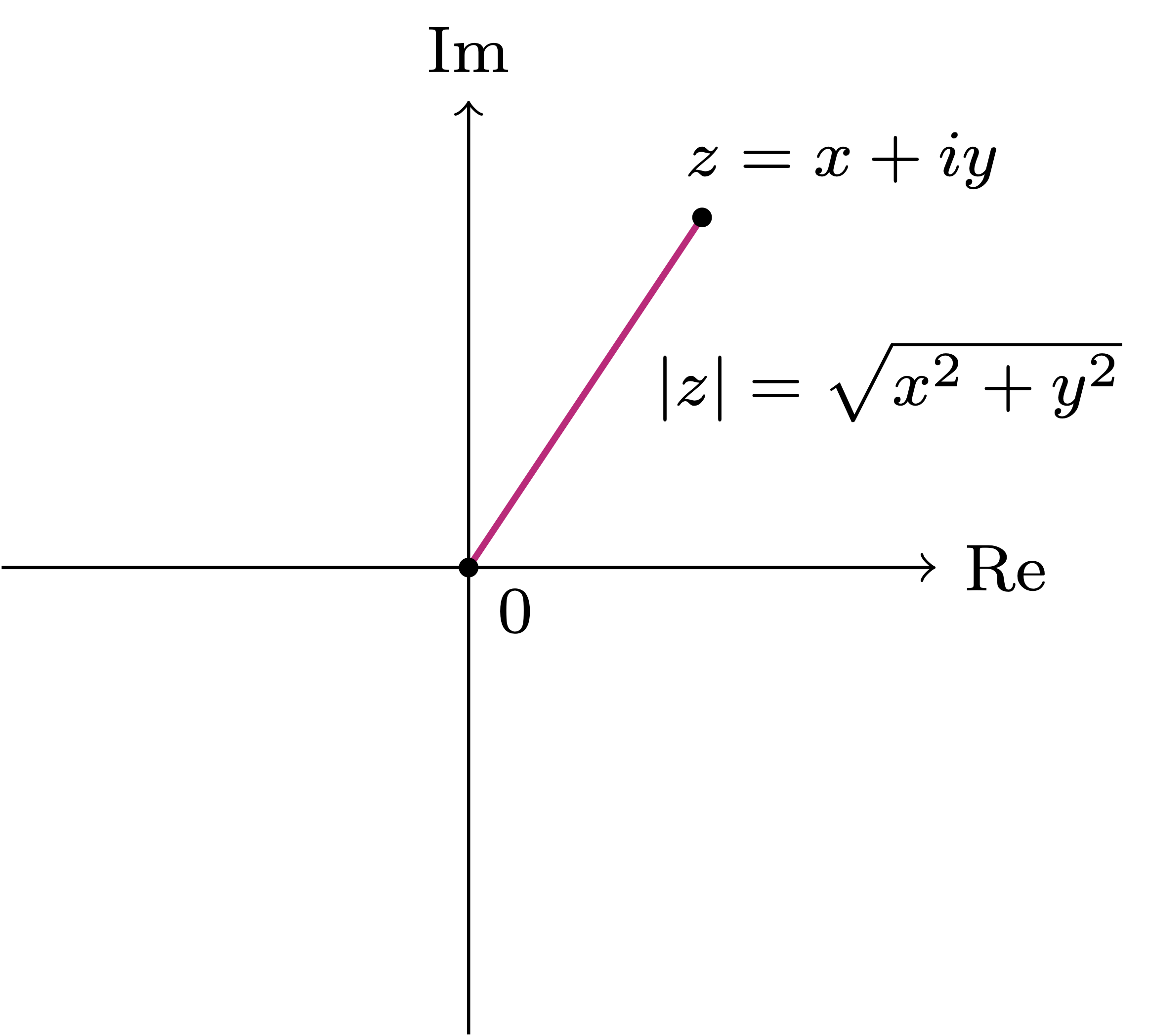
Definition 11: Modulus
Definition 12: Distance in \(\mathbb{C}\)
Theorem 13
Example 14
Solution. The distance is \[\begin{align*} |z- w| & = |(2-4 i)-(-5+i)| \\ & = |7-5 i| \\ & =\sqrt{7^{2}+(-5)^{2}} \\ & =\sqrt{74} \end{align*}\]
Theorem 15
Let \(z, z_{1}, z_{2} \in \mathbb{C}\). Then
\(\left|z_1 \cdot z_2\right|=\left|z_{1}\right|\left|z_{2}\right|\)
\(\left|z^{n}\right|=|z|^{n}\) for all \(n \in \mathbb{N}\)
\(z \cdot \bar{z}=|z|^{2}\)
Theorem 16: Triangle inequality in \(\mathbb{C}\)
For all \(x, y, z \in \mathbb{C}\),
\(|x+y| \leq|x|+|y|\)
\(|x-z| \leq|x-y|+|y-z|\)
4.2 Polar coordinates
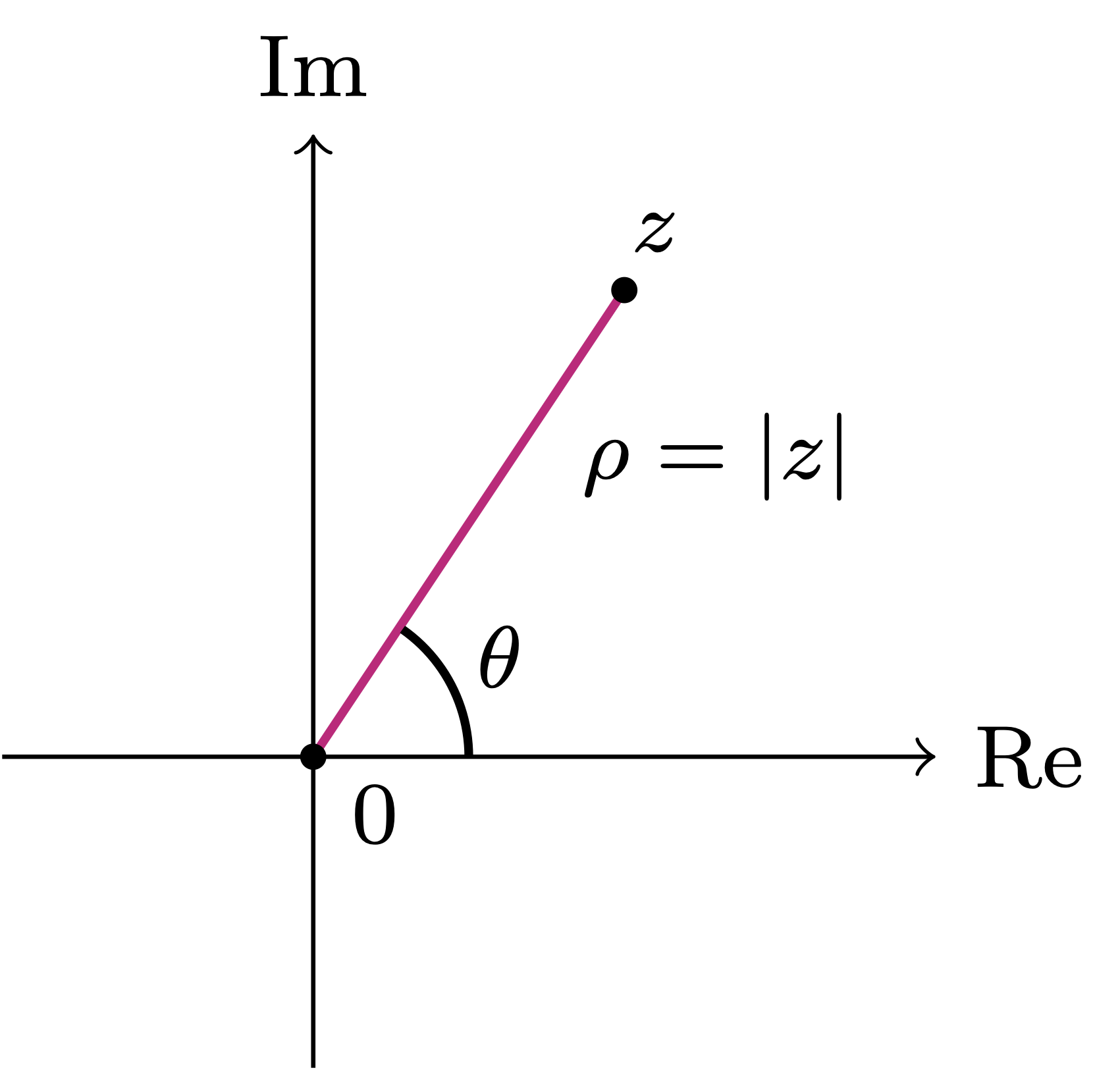
Definition 17: Argument
Example 18
Theorem 19: Polar coordinates
Definition 20: Trigonometric form
Example 21
Solution. We have \[\begin{gather*} x = \rho \cos (\theta) = \sqrt{8} \cos \left( \frac{3}{4} \pi \right) = - \sqrt{8} \cdot \frac{\sqrt{2}}{2} = -2 \\ y = \rho \sin (\theta) = \sqrt{8} \sin \left( \frac{3}{4} \pi \right) = \sqrt{8} \cdot \frac{\sqrt{2}}{2} = 2 \,. \end{gather*}\] Therefore, the cartesian form of \(z\) is \[ z = x + i y = - 2 + 2 i \,. \]
Corollary 22: Computing \(\arg(z)\)
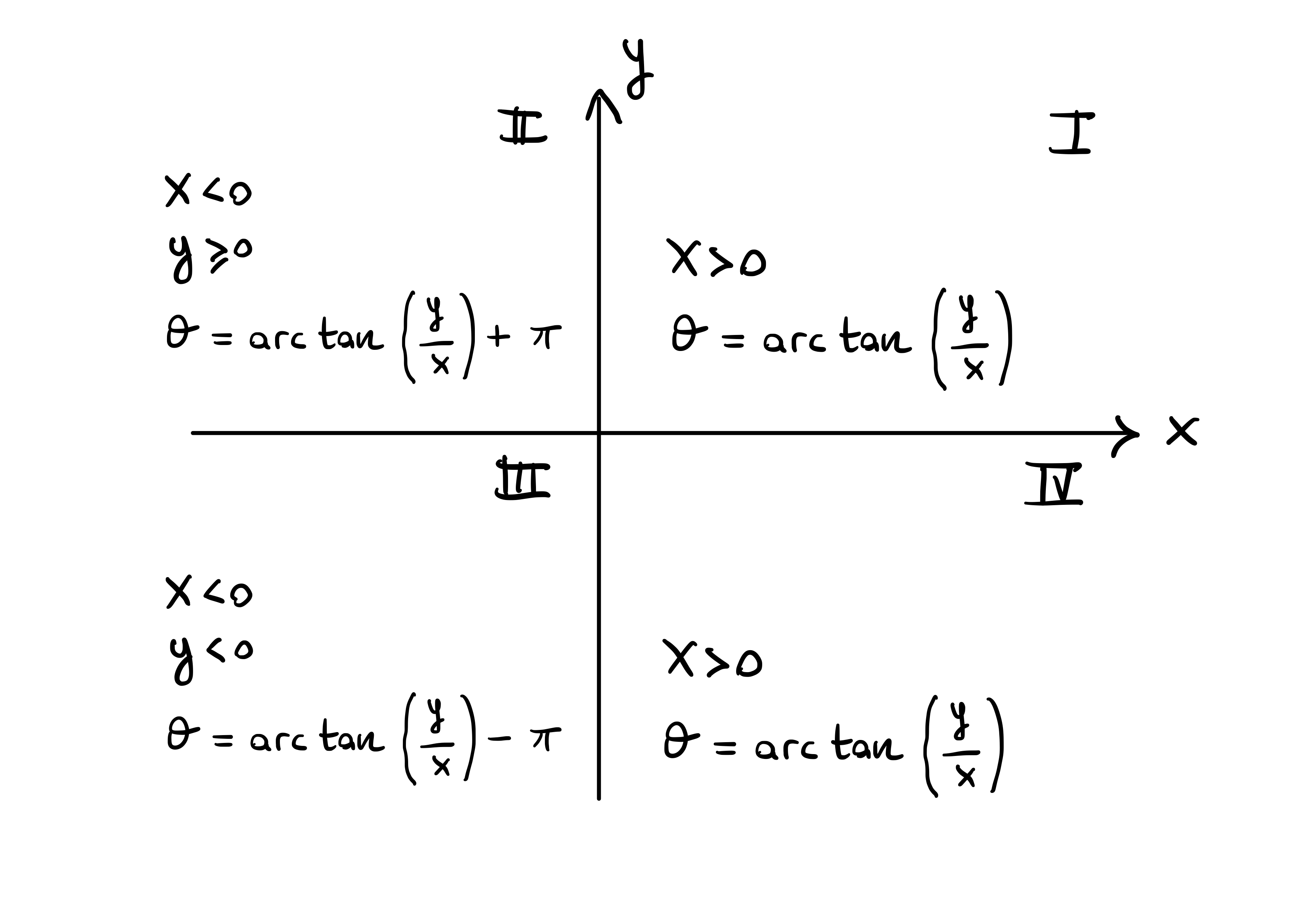
Example 23
Solution. Using the formula for \(\arg\) in Corollary 22 we have \[\begin{align*} \arg (3+4 i) & =\arctan \left(\frac{4}{3}\right) \\ \arg (3-4 i) & =\arctan \left(-\frac{4}{3}\right) = -\arctan \left(\frac{4}{3}\right) \\ \arg (-3+4 i) & = \arctan \left(-\frac{4}{3}\right) + \pi = - \arctan \left(\frac{4}{3}\right) + \pi \\ \arg (-3-4 i) & = \arctan \left(\frac{4}{3}\right) - \pi \end{align*}\]
4.3 Exponential form
Theorem 24: Euler’s identity
Theorem 25
Theorem 26
Definition 27: Exponential form
Example 28
Solution. From Example 21 we know that \(z = -2+2i\) can be written in trigonometric form as \[ z = \sqrt{8} \left[ \cos \left( \frac{3}{4} \pi \right) + i \sin \left( \frac{3}{4} \pi \right) \right] \,. \] By Euler’s identity we hence obtain the exponential form \[ z=\sqrt{8} e^{i \frac{3}{4} \pi} \,. \]
Remark 29: Periodicity of exponential
Proposition 30
Example 31
Question. Compute \((-2+2 i)^{4}\).
Solution. We have two possibilities:
Use the binomial theorem: \[\begin{align*} (-2+2 i)^{4} & =(-2)^{4}+\left(\begin{array}{l} 4 \\ 1 \end{array}\right)(-2)^{3} \cdot 2 i+\left(\begin{array}{l} 4 \\ 2 \end{array}\right)(-2)^{2} \cdot(2 i)^{2} \\ & \quad +\left(\begin{array}{l} 4 \\ 3 \end{array}\right)(-2) \cdot(2 i)^{3}+(2 i)^{4} \\ & =16-4 \cdot 8 \cdot 2 i-6 \cdot 4 \cdot 4+4 \cdot 2 \cdot 8 i+16 \\ & =16-64 i-96+64 i+16=-64 \,. \end{align*}\]
A much simpler calculation is possible by using the exponential form: We know that \[ -2+2 i = \sqrt{8} e^{i \frac{3}{4} \pi} \] by Example 28. Hence \[ (-2+2 i)^{4}=\left(\sqrt{8} e^{i \frac{3}{4} \pi}\right)^{4}=8^{2} e^{i 3 \pi}=-64 \,, \] where we used that \[ e^{i 3 \pi} = e^{i \pi} = \cos(\pi) + i \sin(\pi) = - 1 \] by \(2\pi\) periodicity of \(e^{i\theta}\) and Euler’s identity.
Definition 32: Complex exponential
Theorem 33
Example 34
Solution. We know that \[ |i| = 1 \,, \quad \arg(i) = \frac{\pi}{2} \,. \] Hence we can write \(i\) in exponential form \[ i= |i| e^{i\arg(i)} = e^{i \frac{\pi}{2}} \,. \] Therefore \[ i^{i}=\left(e^{i \frac{\pi}{2}}\right)^{i}=e^{i^2\frac{\pi}{2}}=e^{-\frac{\pi}{2}} \,. \]
4.4 Fundamental Theorem of Algebra
Theorem 35: Fundamental theorem of algebra
Example 36
Solution. The equation \(z^2 = -1\) is equivalent to \[ p(z) = 0 \,, \quad p(z):=z^{2}+1 \,. \] Since \(p\) has degree \(n=2\), the Fundamental Theorem of Algebra tells us that there are two solutions to (4.5). We have already seen that these two solutions are \(z=i\) and \(z=-i\). Then \(p\) factorizes as \[ p(z) = z^{2} + 1 = (z-i)(z+i) \,. \]
Example 37
Solution The associated polynomial equation is \[
p(z) = 0 \,, \quad p(z) := z^4 - 1 \,.
\] Since \(p\) has degree \(n=4\), the Fundamental Theorem of Algebra tells us that there are \(4\) solutions to (4.6). Let us find such solutions. We use the well known identity \[
a^2-b^2 = (a+b)(a-b) \,, \quad \forall \, a,b \in \mathbb{R}\,,
\] to factorize \(p\). We get: \[
p(z) = (z^4-1) = (z^2+1)(z^2-1) \,.
\] We know that \[
z^2 + 1 = 0
\] has solutions \(z = \pm i\). Instead
\[
z^2 - 1 = 0
\] has solutions \(x = \pm 1\). Hence, the four solutions of (4.6) are given by \[
z=1,-1, i,-i \,,
\] and \(p\) factorizes as \[
p(z) = z^4 - 1 = (z-1)(z+1)(z-i)(z+i) \,.
\]
Definition 38: Multiplicity
Example 39
The equation \[ (z-1)(z-2)^{2}(z+i)^{3}=0 \] has 6 solutions:
- \(z=1\) with multiplicity \(1\)
- \(z=2\) with multiplicity \(2\)
- \(z=-i\) with multiplicity \(3\)
4.5 Solving polynomial equations
Proposition 40: Quadratic formula
- If \(\Delta > 0\) then (4.7) has two distinct real solutions \(z_1,z_2 \in \mathbb{R}\) given by \[ z_1 = \frac{-b - \sqrt{\Delta}}{2 a} \,, \quad z_2 = \frac{-b + \sqrt{\Delta}}{2 a} \,. \]
- If \(\Delta = 0\) then (4.7) has one real solution \(z \in \mathbb{R}\) with multiplicity \(2\). Such solution is given by \[ z = z_1 = z_2 = \frac{-b}{2 a} \,. \]
- If \(\Delta < 0\) then (4.7) has two distinct complex solutions \(z_1,z_2 \in \mathbb{C}\) given by \[ z_1 = \frac{-b - i\sqrt{-\Delta}}{2 a} \,, \quad z_2 = \frac{-b + i\sqrt{-\Delta}}{2 a} \,, \] where \(\sqrt{-\Delta} \in \mathbb{R}\), since \(-\Delta>0\).
In all cases, the polynomial at (4.7) factorizes as \[ a z^{2}+b z+c = a (z-z_1)(z-z_2) \,. \]
Example 41
Question. Solve the following equations:
- \(3 z^{2}-6 z+2 = 0\)
- \(4 z^{2}-8 z+4=0\)
- \(z^{2}+2 z+3=0\)
Solution.
We have that \[ \Delta = (-6)^{2}-4 \cdot 3 \cdot 2 = 12 > 0 \] Therefore the equation has two distinct real solutions, given by \[ z=\frac{-(-6) \pm \sqrt{12}}{2 \cdot 3}=\frac{6 \pm \sqrt{12}}{6}=1 \pm \frac{\sqrt{3}}{3} \] In particular we have the factorization \[ 3 z^{2}-6 z+2 = 3 \left( z - 1 - \frac{\sqrt{3}}{3} \right) \left( z - 1 + \frac{\sqrt{3}}{3} \right) \,. \]
We have that \[ \Delta = (-8)^{2}-4 \cdot 4 \cdot 4 = 0 \,. \] Therefore there exists one solution with multiplicity \(2\). This is given by \[ z=\frac{-(-8)}{2 \cdot 4} = 1 \,. \] In particular we have the factorization \[ 4 z^{2}-8 x+4 = 4 (z-1)^2 \,. \]
We have \[ \Delta = 2^{2}-4 \cdot 1 \cdot 3 = - 8 < 0 \,. \] Therefore there are two complex solutions given by \[ z=\frac{-2 \pm i \sqrt{8}}{2 \cdot 1} = -1 \pm i \sqrt{2} \,. \] In particular we have the factorization \[ z^{2}+2 z+3 = (z + 1 - i \sqrt{2}) (z + 1 + i\sqrt{2}) \,. \]
Proposition 42: Quadratic formula with complex coefficients
Example 43
Solution. We have \[\begin{align*} \Delta & = (-(3+i))^{2}-4 \cdot \frac{1}{2} \cdot(4-i) \\ & = 8+6 i-8+2 i \\ & =8 i \,. \end{align*}\] Therefore \(\Delta \in \mathbb{C}\). We have to find solutions \(S_1\) and \(S_2\) to the equation \[ z^2 = \Delta = 8i \,. \tag{4.9}\] We look for solutions of the form \(z=a+ i b\). Then we must have that \[ z^{2}=(a+ ib)^{2}=a^{2}-b^{2}+2 a b i = 8 i \,. \] Thus \[ a^{2}-b^{2}=0 \,, \quad 2 a b = 8 \,. \] From the first equation we conclude that \(|a|=|b|\). From the second equation we have that \(ab=4\), and therefore \(a\) and \(b\) must have the same sign. Hence \(a=b\), and \[ 2 a b = 8 \quad \implies \quad a = b = \pm 2 \,. \] From this we conclude that the solutions to (4.9) are \[ S_{1} = 2+2 i \,, \quad S_{2}=-2-2 i \,. \] Hence the solutions to (4.8) are \[\begin{align*} z_1 & = \frac{3+i+S_{1}}{2 \cdot \frac{1}{2}} = 3 + i + S_{1} \\ & = 3 + i + 2 + 2i = 5 + 3i \,, \end{align*}\] and \[\begin{align*} z_2 & = \frac{3+i+S_{2}}{2 \cdot \frac{1}{2}} = 3+i+S_{2} \\ & = 3+i -2 - 2i = 1 - i \,. \end{align*}\] In particular, the given polynomial factorizes as \[\begin{align*} \frac{1}{2} z^{2}-(3+i) z+(4-i) & = \frac12 (z - z_1)(z-z_2) \\ & = \frac12 (z - 5 - 3i)(z - 1 + i) \,. \end{align*}\]
Example 44
Question. Consider the equation \[ z^{3}-7 z^{2}+6 z=0 \,. \]
- Check whether \(z=0,1,-1\) are solutions.
- Using your answer from Point 1, and polynomial division, find all the solutions.
Solution.
By direct inspection we see that \(z=0\) and \(z=1\) are solutions.
Since \(z = 0\) is a solution, we can factorize \[ z^{3}-7 z^{2}+6 z=z\left(z^{2}-7 z+6\right) \,. \] We could now use the quadratic formula on the term \(z^{2}-7 z+6\) to find the remaining two roots. However, we have already observed that \(z=1\) is a solution. Therefore \(z-1\) divides \(z^{2}-7 z+6\). Using polynomial long division, see Figure 4.4, we find that \[ \frac{z^{2}-7 z+6}{z-1}=z-6 \,. \] Therefore the last solution is \(z=6\), and \[ z^{3}-7 z^{2}+6 z=z(z-1)(z-6) \,. \]
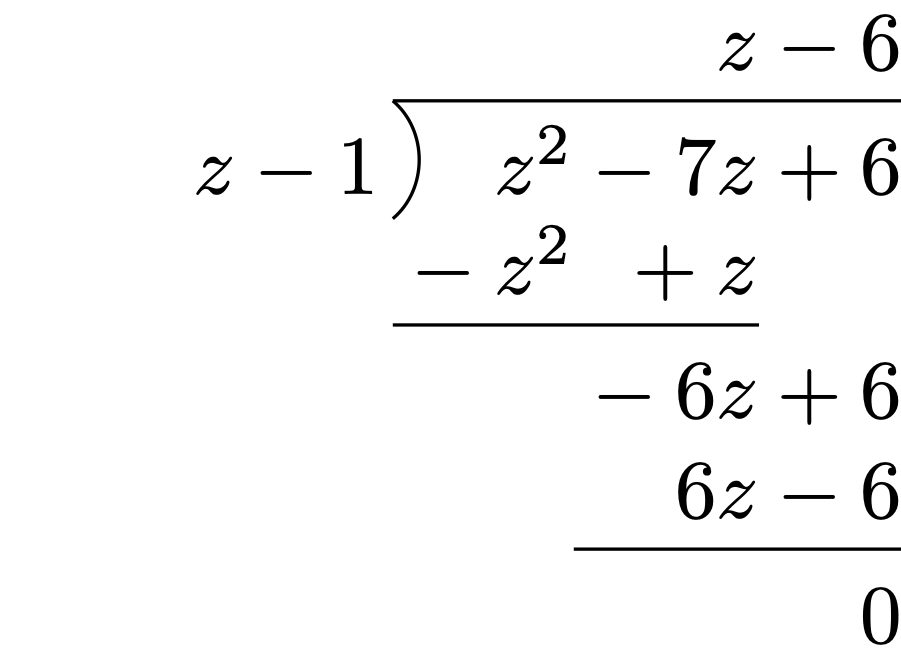
Example 45
Solution. It is easy to see \(z=1\) is a solution. This means that \(z-1\) divides \(z^{3}-7 z+6\). By using polynomial long division, see Figure 4.5, we compute that \[ \frac{z^{3}-7 z+6}{z-1}=z^{2}+z-6 \,. \] We are now left to solve \[ z^{2}+z-6 = 0\,. \] Using the quadratic formula, we see that the above is solved by \(z=2\) and \(z=-3\). Therefore the given polynomial factorizes as \[ z^{3}-7 z+6 = (z-1)(z-2)(z+3) \,. \]
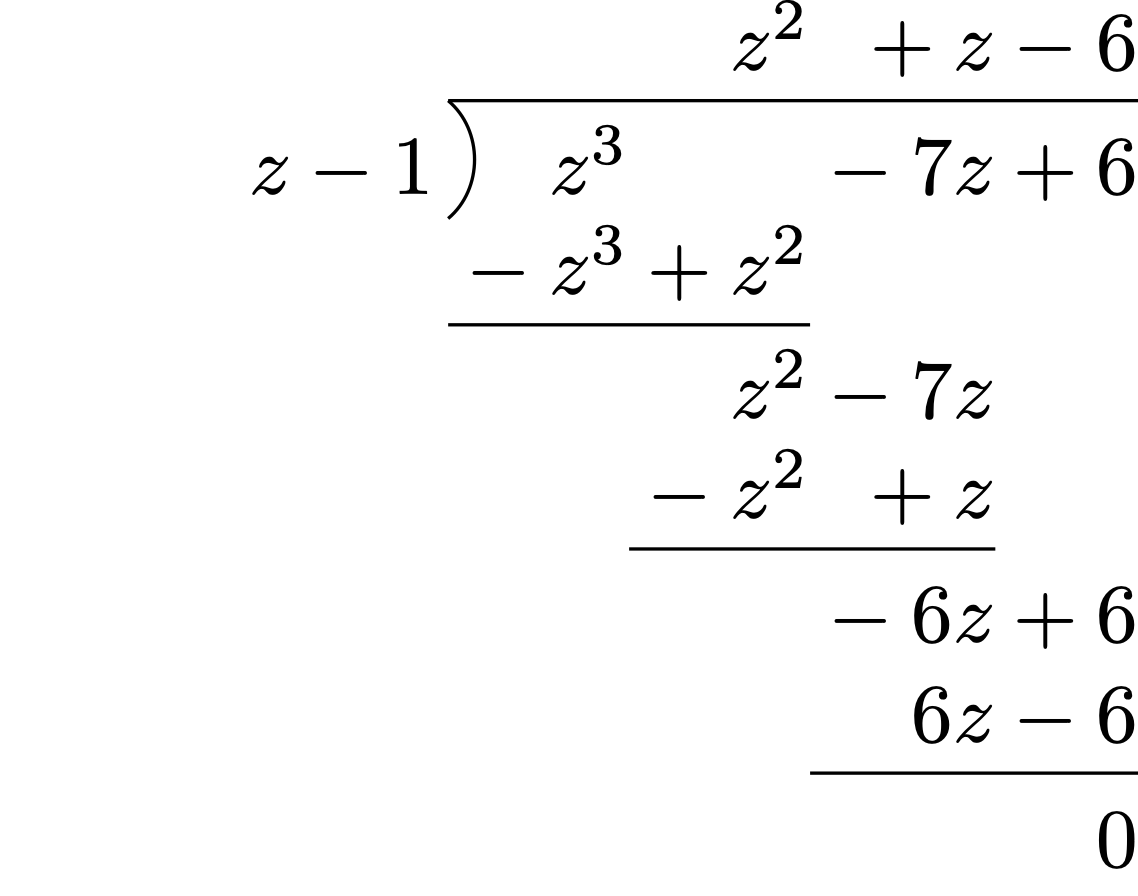
4.6 Roots of unity
Theorem 46
Definition 47
Example 48
Solution. The \(4\) solutions are given by \[ z_k = \exp \left(i \frac{2 \pi k}{4} \right) = \exp \left(i \frac{\pi k}{2} \right) \,, \] for \(k=0,1,2,3\). We compute: \[\begin{align*} z_0 & = e^{i 0} = 1 \,, & \quad & z_1 = e^{i \frac{\pi}{2}}=i \,, \\ z_2 & = e^{i \pi}=-1 \,, & \quad & z_3 = e^{i \frac{3 \pi}{2}}=-i \, . \end{align*}\] Note that for \(k=4\) we would again get the solution \(z=e^{i 2 \pi}=1\).
Example 49
Solution. The \(3\) solutions are given by \[ z_k = \exp \left( i \frac{2 \pi k}{3} \right) \,, \] for \(k=0,1,2\). We compute: \[ z_0=e^{i 0}=1, \quad z_1=e^{i \frac{2 \pi}{3}}, \quad z_2=e^{i \frac{4 \pi}{3}} . \] We can write \(z_1\) and \(z_2\) in cartesian form: \[ z_1 = e^{i \frac{2 \pi}{3}}=\cos \left(\frac{2 \pi}{3}\right)+i \sin \left(\frac{2 \pi}{3}\right)=-\frac{1}{2}+\frac{\sqrt{3}}{2} i \] and \[ z_2 = e^{i \frac{4 \pi}{3}}=\cos \left(\frac{4 \pi}{3}\right)+i \sin \left(\frac{4 \pi}{3}\right)=-\frac{1}{2}-\frac{\sqrt{3}}{2} i \,. \]
4.7 Roots in \(\mathbb{C}\)
Theorem 50
Example 51
Solution. Let \(c = -32\). We have \[ |c| = |-32|=32=2^{5}\,, \quad \theta = \arg (-32)=\pi \,. \] The \(5\) solutions are given by \[ z_k = \left(2^{5}\right)^{\frac{1}{5}} \exp \left(i \pi \, \frac{1+2 k}{5} \right) \,, \quad k \in \mathbb{Z}\,, \] for \(k=0,1,2,3,4\). We get \[\begin{align*} z_0 & = 2 e^{i \frac{\pi}{5}} \, & \quad & z_1 = 2 e^{i \frac{3 \pi}{5}} \\ z_2 & = 2 e^{i \pi}=-2 \, & \quad & z_3=2 e^{i \frac{7 \pi}{5}} \\ z_4 &= 2 e^{i \frac{9 \pi}{5}} & \quad & \end{align*}\]
Example 52
Solution. Set \[ c:=9\left(\cos \left(\frac{\pi}{3}\right)+i \sin \left(\frac{\pi}{3}\right)\right) \,. \] The complex number \(c\) is already in the trigonometric form, so that we can immediately obtain \[ |c| = 9 \,, \quad \theta = \arg(c) = \frac{\pi}{3} \,. \] The \(4\) solutions are given by \[\begin{align*} z_k & = \sqrt[4]{9} \, \exp \left( i \, \frac{ \pi/3 + 2 \pi k}{4} \right) \\ & = \sqrt{3} \exp \left( i \pi \, \frac{1+6 k}{12} \right) \end{align*}\] for \(k=0,1,2,3\). We compute \[\begin{align*} z_0 & = \sqrt{3} e^{i \pi \frac{1}{12}} & \quad & z_1 = \sqrt{3} e^{i \pi \frac{7}{12}} \\ z_2 & = \sqrt{3} e^{i \pi \frac{13}{12}} & \quad & z_3 = \sqrt{3} e^{i \pi \frac{19}{12}} \end{align*}\]