1  Introduction

The first aim of this lecture notes is to rigorously introduce the set of real numbers, which is denoted by \(\mathbb{R}\). But what do we mean by real numbers? To start our discussion, introduce the set of natural numbers (or non-negative integers) \[ \mathbb{N}= \{0,1,2,3,4,5,\dots\} \]

On this set we have a notion of sum of two numbers, denoted as usual by \[ n+m \]

for \(n,m \in \mathbb{N}\). Here the symbol \(\in\) denotes that \(m\) and \(n\) belong to \(\mathbb{N}\). For example \(3+7\) results in \(10\).

Question 1

Can the sum be inverted? That is, given any \(n,m \in \mathbb{N}\), can you always find \(x \in \mathbb{N}\) such that \[ n+x = m \,? \tag{1.1}\]

Of course to invert (1.1) we can just perform a subtraction, implying that

\[ x = m - n \,. \]

But there is a catch. In general \(x\) does not need to be in \(\mathbb{N}\). For example, take \(n=10\) and \(m=1\). Then \(x = -9\), which does not belong to \(\mathbb{N}\). Therefore the answer to Question 1 is NO.

To make sure that we can always invert the sum, we need to extend the set \(\mathbb{N}\). This is done simply by introducing the set of integers \[ \mathbb{Z}:= \{ -n,n \, \colon \, n \in \mathbb{N}\} \,, \]

that is, the set

\[ \mathbb{Z}:= \{ \ldots, -3,-2,-1,0,1,2,3,\ldots \} \,. \]

The sum can be extended to \(\mathbb{Z}\), by defining \[ (-n) + (-m) := - (m+n) \tag{1.2}\]

for all \(m,n \in \mathbb{N}\). Now every element of \(\mathbb{Z}\) possesses an inverse, that is, for each \(n \in \mathbb{Z}\), there exists \(m \in \mathbb{Z}\), such that \[ n + m = 0 \,. \]

Can we characterize \(m\) explicitly? Of course! Seeing the definition at (1.2), we simply have \[ m = - n \,. \]

On the set \(\mathbb{Z}\) we can also define the operation of multiplication, in the usual way we learnt in school. For \(n,m \in \mathbb{Z}\), we denote the multiplication by \(nm\) or \(n \cdot m\). For example \(7 \cdot 2 = 14\) and \(1 \cdot (-1) = -1\).

Question 2

Can the multiplication in \(\mathbb{Z}\) be inverted? That is, given any \(n,m \in \mathbb{Z}\), can you always find \(x \in \mathbb{Z}\) such that \[ nx = m \,? \tag{1.3}\]

To invert (1.3) if \(n \neq 0\), we can just perform a division, to obtain \[ x = \frac{m}{n} \,. \] But again there is a catch. Indeed taking \(n=2\) and \(m=1\) yields \(x = 1/2\), which does not belong to \(\mathbb{Z}\). The answer to Question 2 is therefore NO.

Thus, in order to invert the multiplication, we need to extend the set of integers \(\mathbb{Z}\). This extension is called the set of rational numbers, defined by \[ \mathbb{Q}:= \left\{ \frac{m}{n} \, \colon \, m,n \in \mathbb{Z}, \, n \neq 0 \right\} \,. \] We then extend the operations of sum and multiplication to \(\mathbb{Q}\) by defining \[ \frac{m}{n} + \frac{p}{q} := \frac{mq + np}{nq} \] and \[ \frac{m}{n} \, \cdot \, \frac{p}{q} := \frac{mp}{nq} \] Now the multiplication is invertible in \(\mathbb{Q}\). Specifically, each non-zero element has an inverse: the inverse of \(m/n\) is given by \(n/m\).

To summarize, we have extended \(\mathbb{N}\) to \(\mathbb{Z}\), and \(\mathbb{Z}\) to \(\mathbb{Q}\). By construction we have \[ \mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\,. \] Moreover sum and product are invertible in \(\mathbb{Q}\). Now we are happy right? So and so.

Question 3

Can we draw the set \(\mathbb{Q}\)?

It is clear how to draw \(\mathbb{Z}\), as seen below.

Figure 1.1: Representation of integers \(\mathbb{Z}\)

However \(\mathbb{Q}\) is much larger than the set \(\mathbb{Z}\) represented by the ticks in Figure 1.1. What do we mean by larger? For example, consider \(0 \in \mathbb{Q}\).

Question 4

What is the number \(x \in \mathbb{Q}\) which is closest to \(0\)?

There is no right answer to the above question, since whichever rational number \(m/n\) you consider, you can always squeeze the rational number \(m / (2n)\) in between: \[ 0 < \frac{m}{2n} < \frac{m}{n} \,. \] For example think about the case of the numbers \[ \frac1n \, \text{ for } \, n \in \mathbb{N}, \, n \neq 0 \,. \] Such numbers get arbitrarily close to \(0\), as depicted below.

Fractions \(\frac{1}{n}\) can get arbitrarily close to \(0\)

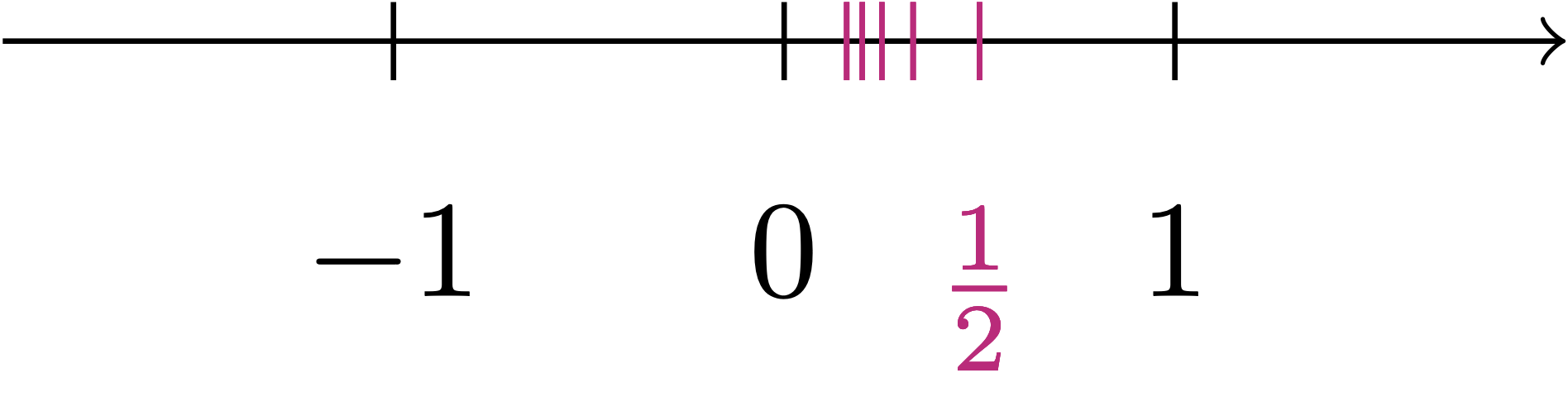
Maybe if we do the same reasoning with other progressively smaller rational numbers, we manage to fill out the interval \([0,1]\). In other words, we might conjecture the following.

Conjecture 5

Maybe \(\mathbb{Q}\) can be represented by a continuous line.

Do you think the above conjecture is true? If it was, mathematics would be quite boring. Indeed Conjecture 5 is false, as shown by the Theorem below.

Theorem 6

The number \(\sqrt{2}\) does not belong to \(\mathbb{Q}\).

Theorem 6 is the reason why \(\sqrt{2}\) is called an irrational number. For reference, a few digits of \(\sqrt{2}\) are given by \[ \sqrt{2} = 1.414213562373095048\ldots \] and the situation is as in the picture below.

Representing \(\sqrt{2}\) on the numbers line.

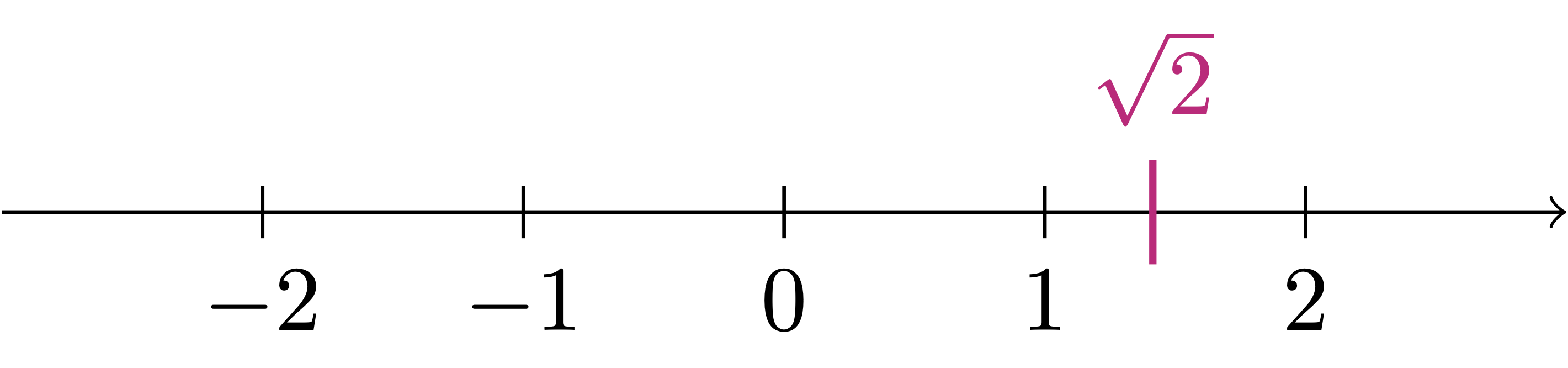
We can therefore see that Conjecture 5 is false, and \(\mathbb{Q}\) is not a line: indeed \(\mathbb{Q}\) has a gap at \(\sqrt{2}\). Let us see why Theorem 6 is true.

Proof: Proof of Theorem 6

We prove that \[ \sqrt{2} \notin \mathbb{Q} \] by contradiction.

Wait, what does this mean? Proving the claim by contradiction means assuming that the claim is false. This means we assume that \[ \sqrt{2} \in \mathbb{Q}\,. \tag{1.4}\] From this assumption we then start deducing other statements, hoping to encounter a statement which is FALSE. But if (1.4) leads to a false statement, then it must be that (1.4) is FALSE. Thus the contrary of (1.4) must hold, meaning that \[ \sqrt{2} \notin \mathbb{Q} \] as we wanted to show. This would conclude the proof.

Now we need to actually show that (1.4) will lead to a contradiction. Since this is our first proof, let us take it slowly, step-by-step.

1. Assuming (1.4) just means that there exists \(q \in \mathbb{Q}\) such that \[ q = \sqrt{2} \, . \tag{1.5}\]

2. Since \(q \in \mathbb{Q}\), by definition we have \[ q = \frac{m}{n} \] for some \(m,n \in \mathbb{N}\) with \(n \neq 0\).

3. Recalling (1.5), we then have \[ \frac{m}{n} = \sqrt{2} \,. \]

4. We can square the above equation to get \[ \frac{m^2}{n^2} = 2 \,. \tag{1.6}\]

5. Withouth loss of generality, we can assume that \(m\) and \(n\) have no common factors.

   Wait. What does Step 5 mean? You will encounter the sentence withouth loss of generality many times in mathematics. It is often abbreviated in WLOG. WLOG means that the assumption that follows is chosen arbitrarily, but does not affect the validity of the proof in general.
   For example in our case we can assume that \(m\) and \(n\) have no common factor. This is because if \(m\) and \(n\) had common factors, then it would mean \[ m = a \tilde{m} \,, \quad n = a \tilde{n} \] for some \(a \in \mathbb{N}\) with \(a \neq 0\). Then \[ \frac{m}{n} = \frac{ a \tilde{m} }{ a \tilde{n} } = \frac{ \tilde{m} }{ \tilde{n} } \,. \] Therefore by (1.6) \[ \frac{ \tilde{m}^2 }{ \tilde{n}^2 } = 2 \,. \] The proof can now proceed in the same way we would have proceeded from Step 4, but in addition we have the hypothesis that \(\tilde{m}\) and \(\tilde{n}\) have no common factors.

6. Equation (1.6) implies \[ m^2 = 2 n^2 \,. \tag{1.7}\] Therefore the integer \(m^2\) is an even number.

   Why is \(m^2\) even? As you already know, even numbers are \[ 0, 2, 4, 6, 8, 10, 12, \ldots \] All these numbers have in common that they can be divided by \(2\), and so they can be written as \[ 2 p \] for some \(p \in \mathbb{N}\). For example \(52\) is even, because \[ 52 = 2 \cdot 26 \,. \] Instead, odd numbers are \[ 1, 3, 5, 7, 8, 9, 11, \ldots \] These can be all written as \[ 2p + 1 \] for some \(p \in \mathbb{N}\). For example \(53\) is odd, because \[ 52 = 2 \cdot 26 + 1 \,. \]

7. Thus \(m\) is an even number, and so there exists \(p \in \mathbb{N}\) such that \[ m = 2p \,. \tag{1.8}\]

   Why is (1.8) true? Let us see what happens if we take the square of an even number \(m = 2p\) \[ m^2 = (2p)^2 = 4p^2 = 2 (2p^2) = 2 q \,. \] Thus \(m^2 = 2 q\) for some \(q\in \mathbb{N}\), and so \(m^2\) is an even number. If instead \(m\) is odd, then \(m = 2p + 1\) and \[ m^2 = (2p + 1 )^2 = 4p^2 + 4p + 1 = 2(2 p^2 + 2p) + 1 \] showing that also \(m^2\) is odd.
   This justifies Step 7: Indeed we know that \(m^2\) is an even number from Step 6. If \(m\) was odd, then \(m^2\) would be odd. Hence \(m\) must be even as well.

8. If we substitute (1.8) in (1.7) we get \[ m^2 = 2n^2 \, \implies \, (2p)^2 = 2n^2 \, \implies \, 4 p^2 = 2 n^2 \] Dividing both terms by \(2\), we obtain \[ n^2 = 2p^2\,. \tag{1.9}\]

9. We now make a series of observations:

   • Equation (1.9) says that \(n^2\) is even.
   • Step 6 says that \(m^2\) is even.
   • Therefore \(n\) and \(m\) are also even.
     
   • Hence \(n\) and \(m\) have \(2\) as common factor.
   • But Step 5 says that \(n\) and \(m\) have no common factors.
   • CONTRADICTION

10. Our reasoning has run into a contradiction, starting from assumption (1.4), which says that \[ \sqrt{2} \in \mathbb{Q}\,. \] Hence the above must be FALSE, and so \[ \sqrt{2} \notin \mathbb{Q}\, \] ending the proof.

Seeing that \(\sqrt{2} \notin \mathbb{Q}\), we might be tempted to just fill in the gap by adding \(\sqrt{2}\) to \(\mathbb{Q}\). However, with analogous proof to Theorem 6, we can prove that \[ \sqrt{p} \notin \mathbb{Q} \] for each prime number \(p\). As there are infinite prime numbers, this means that \(\mathbb{Q}\) has infinite gaps. Then we might attempt to fill in these gaps via the extension \[ \tilde{\mathbb{Q}} := \mathbb{Q}\cup \{ \sqrt{p} \, \colon \, p \, \text{ prime} \} \,. \] However even this is not enough, as we would still have numbers which are not contained in \(\tilde{Q}\), for example \[ \sqrt{2} + \sqrt{3} , \, \pi , \, \pi + \sqrt{2} \notin \tilde{\mathbb{Q}} \,. \]

Remark 7

Proving that \[ \sqrt{2} + \sqrt{3} \notin \mathbb{Q} \] is relatively easy, and will be left as an exercise. Instead, proving that \[ \pi \notin \mathbb{Q} \] is way more complicated. There are several proof of the fact, all requiring mathematics which is more advanced of the one presented in this course. For some proofs, see this Wikipedia page.

The reality of things is that to complete \(\mathbb{Q}\) and make it into a continuous line we have to add a lot of points. Indeed, we need to add way more points than the ones already contained in \(\mathbb{Q}\). Such extension of \(\mathbb{Q}\) will be called \(\mathbb{R}\), the set of real numbers. The inclusions will therefore be \[ \mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}\,. \] The set \(\mathbb{R}\) is not at all trivial to construct. In fact, at first we will not construct it, but just do the following:

• We will assume that \(\mathbb{R}\) exists and satisfies some basic axioms.
• One of the axioms is that \(\mathbb{R}\) fills all the gaps that \(\mathbb{Q}\) has. Therefore \(\mathbb{R}\) can be thought as a continuous line.
• We will study the properties of \(\mathbb{R}\) which descend from such axioms.

For example one of the properties of \(\mathbb{R}\) will be the following:

Theorem 8: We will prove this in the future

\(\mathbb{R}\) contains all the square roots. This means that for every \(x \in \mathbb{R}\) with \(x \geq 0\), we have \[ \sqrt{x} \in \mathbb{R}\,. \]

At the end of this chapter we will provide a concrete model for the real numbers \(\mathbb{R}\), to prove once and for all that such set indeed exists.

Theorem 9: We will prove this in the future

There exists a set \(\mathbb{R}\), called the set of real numbers, which has the following properties:

• \(\mathbb{R}\) extends \(\mathbb{Q}\), that is, \[ \mathbb{Q}\subset \mathbb{R}\,. \]
• \(\mathbb{R}\) satisfies certain axioms.
• \(\mathbb{R}\) fills all the gaps that \(\mathbb{Q}\) has. In particular \(\mathbb{R}\) can be represented by a continuous line.