4 Surfaces
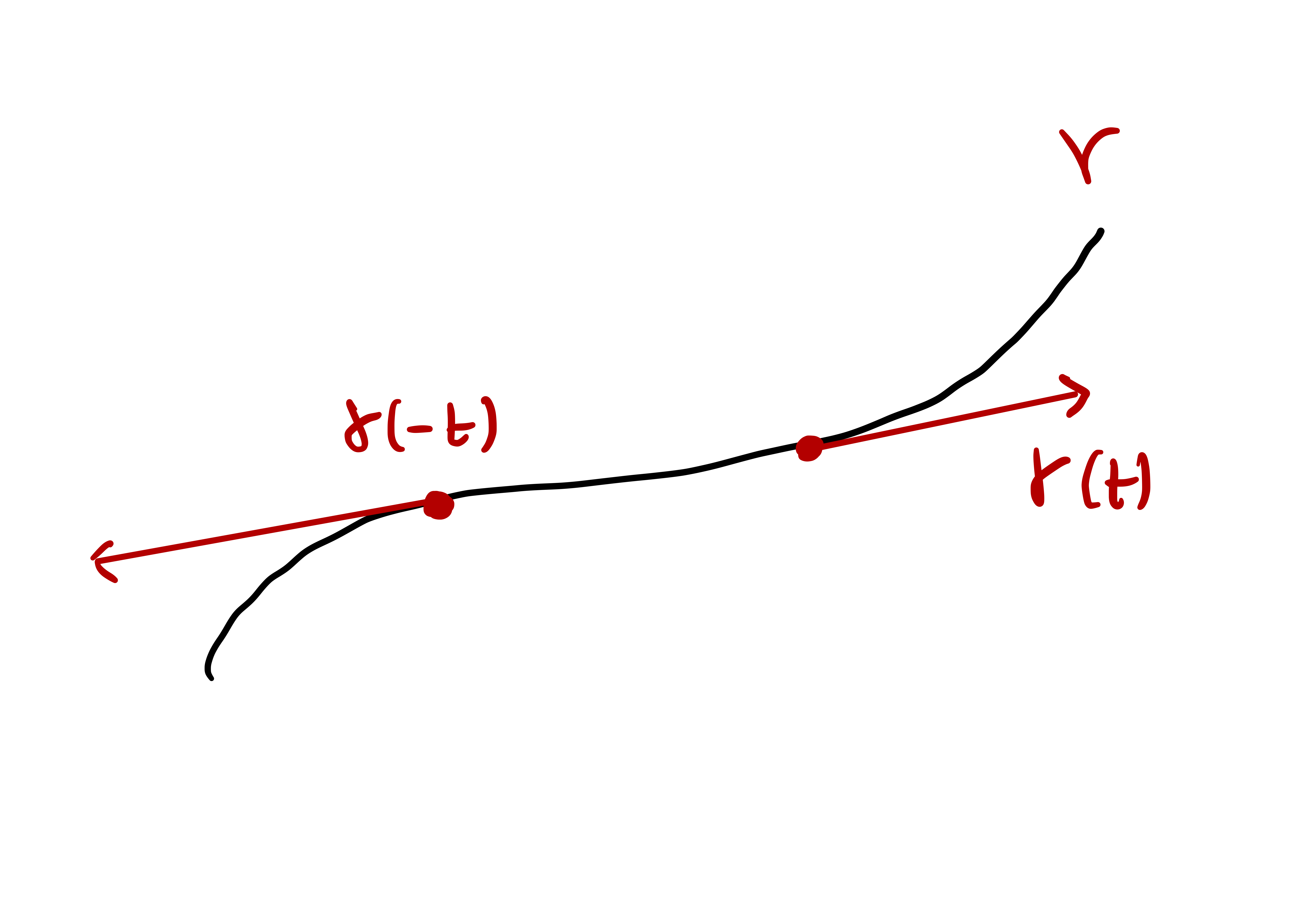
Curves are 1D objects in \(\mathbb{R}^3\), parametrized via functions \({\pmb{\gamma}}\colon (a,b) \to \mathbb{R}^3\). There is only one available direction in which to move on a curve:
- \(t \mapsto {\pmb{\gamma}}(t)\) moves forward on the curve
- \(t \mapsto {\pmb{\gamma}}(-t)\) moves backward on the curve
Surfaces are 2D objects in \(\mathbb{R}^3\). There are two directions in which one can move on a surface.
Question 1
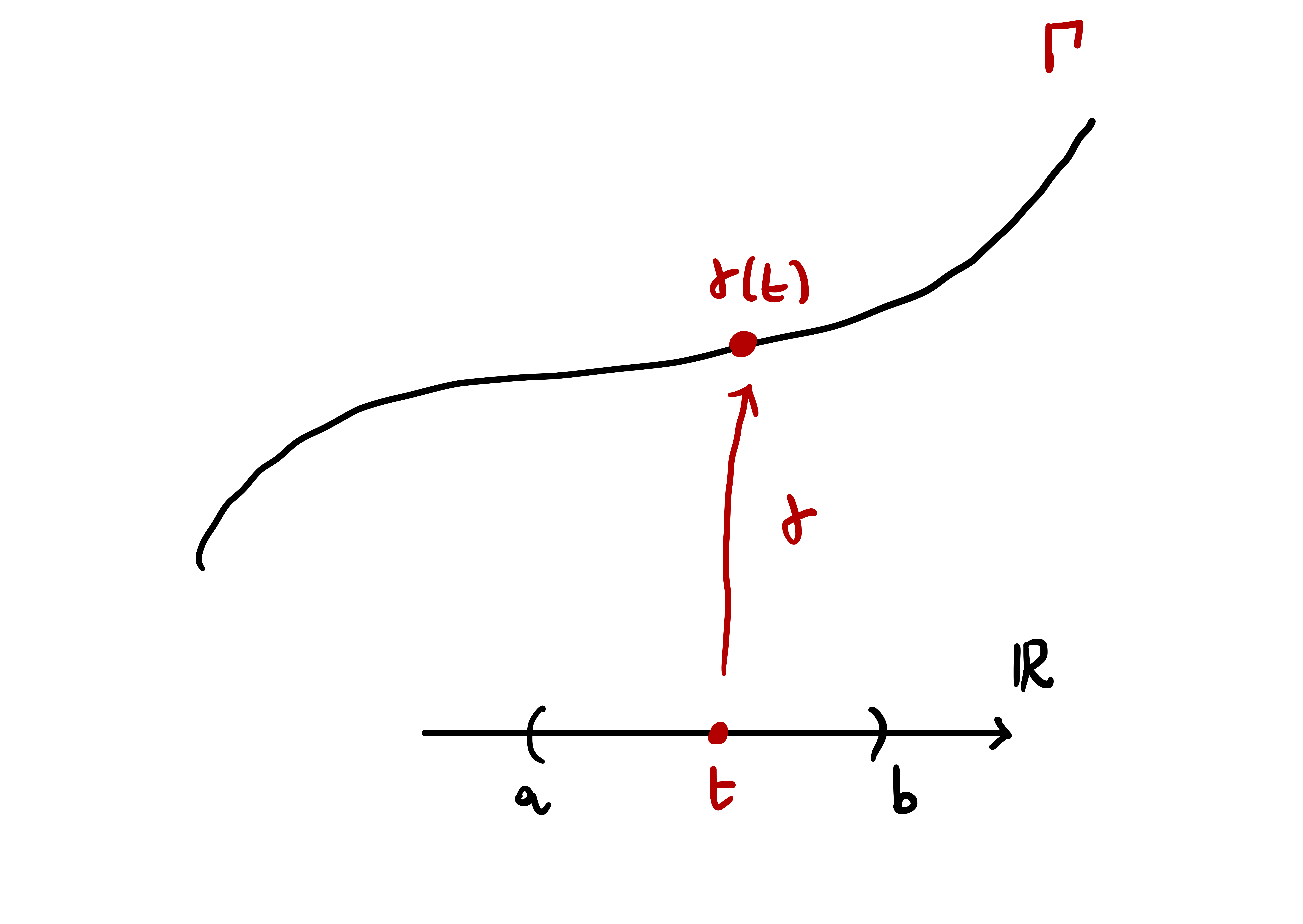
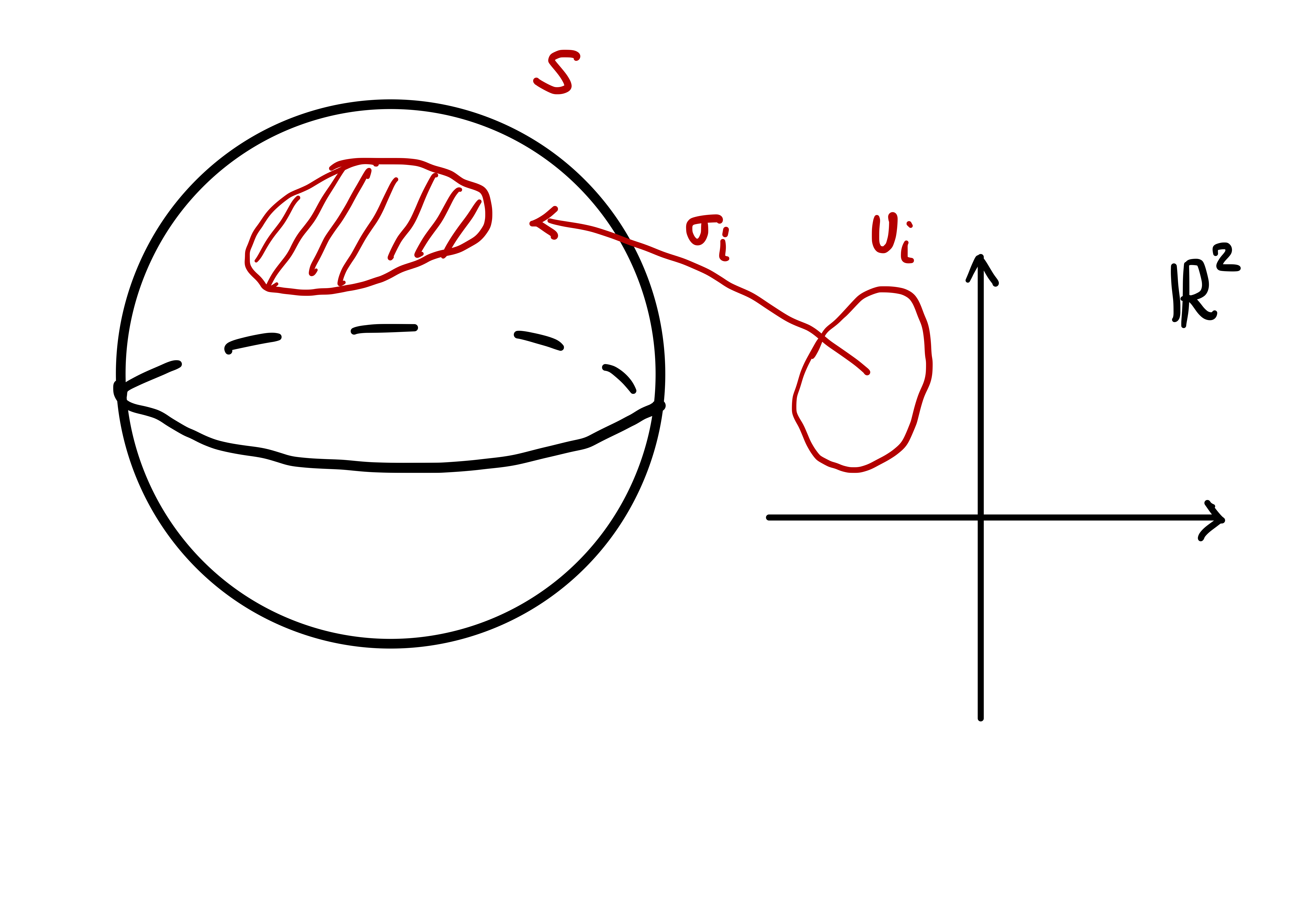
A curve \(\Gamma \subseteq \mathbb{R}^3\) can be described with one function \({\pmb{\gamma}}\colon (a,b) \to \Gamma\). The idea is that \(\Gamma\) looks locally like \(\mathbb{R}\).
A surface \(\mathcal{S}\) cannot be described, in general, with just one function \({\pmb{\sigma}}\colon U \to \mathcal{S}\), with \(U \subseteq \mathbb{R}^2\) open set. The idea is that, to describe \(\mathcal{S}\), one needs to piece together many local charts \({\pmb{\sigma}}_i \colon U_i \to \mathcal{S}\) with \(U_i \subseteq \mathbb{R}^2\) open. Such charts have to cover the whole surface \(\mathcal{S}\), e.g. \[ \mathcal{S}= \bigcup_{i} {\pmb{\sigma}}_i (U_i) \,. \]
4.1 Preliminaries
Before proceeding with the formal definition of surface, we need to establish some basic notation and terminology regarding linear algebra, the topology of \(\mathbb{R}^n\), and calculus for smooth maps from \(\mathbb{R}^n\) into \(\mathbb{R}^m\).
4.1.1 Linear algebra
Definition 2: Bilinear form
\(B\) is bilinear if \[\begin{align*} B(\lambda_1 \mathbf{v}_1 + \lambda_2 \mathbf{v}_2 , \mathbf{w}) & = \lambda_1 B(\mathbf{v}_1,\mathbf{w}) + \lambda_2 B(\mathbf{v}_2,\mathbf{w}) \,, \\ B(\mathbf{w}, \lambda_1 \mathbf{v}_1 + \lambda_2 \mathbf{v}_2 ) & = \lambda_1 B(\mathbf{w},\mathbf{v}_1) + \lambda_2 B(\mathbf{w}, \mathbf{v}_2) \,. \end{align*}\] for all \(\mathbf{v}_i,\mathbf{w}\in V\), \(\lambda_i \in \mathbb{R}\).
\(B\) is symmetric if \[ B(\mathbf{v},\mathbf{w}) = B(\mathbf{w}, \mathbf{v}) \] for all \(\mathbf{v},\mathbf{w}\in V\).
A bilinear map \(B\) is called bilinear form on \(V\).
Notation
Bilinear forms can be represented by a matrix.
Remark 3: Matrix representation for bilinear forms
Let \(\{\mathbf{v}_1, \ldots , \mathbf{v}_n \}\) be a basis for the vector space \(V\). Given a bilinear form \(B \colon V \times V \to \mathbb{R}\) we define the matrix \[ M := \left( B(\mathbf{v}_i,\mathbf{v}_j) \right)_{i,j=1}^n \in \mathbb{R}^{n \times n} \,. \] Then \[ B(\mathbf{v},\mathbf{w}) = \mathbf{x}^T \,M \, \mathbf{y}\,. \]
Proof. We can write \(\mathbf{v}\) and \(\mathbf{w}\) in cordinates as \[ \mathbf{v}= \sum_{i=1}^n \lambda_i \mathbf{v}_i \,, \quad \mathbf{w}= \sum_{i=1}^n \mu_i \mathbf{v}_i \,, \] for suitable coefficients \(\lambda_i, \mu_i \in \mathbb{R}\). Using bilinearity of \(B\) we get \[\begin{align*} B(\mathbf{v},\mathbf{w}) & = B \left( \sum_{i=1}^n \lambda_i \mathbf{v}_i, \sum_{j=1}^n \mu_j \mathbf{v}_j \right) \\ & = \sum_{i,j=1}^n \lambda_i \mu_j B(\mathbf{v}_i,\mathbf{v}_j) \\ & = \mathbf{x}^T M \mathbf{y}\,. \end{align*}\]
Definition 4: Quadratic form
A symmetric bilinear form is uniquely determinded by its quadratic form, as stated in the following proposition.
Proposition 5
The proof is an easy check, and is left as an exercise.
Definition 6: Inner product
Let \(V\) be a vector space. An inner product on \(V\) is a symmetric bilinear form \(\left\langle \cdot,\cdot \right\rangle \colon V \times V \to \mathbb{R}\) such that \[ \left\langle \mathbf{v},\mathbf{v} \right\rangle > 0 \,, \quad \forall \, \mathbf{v}\in V \,. \] Moreover:
The length of a vector \(\mathbf{v}\in V\) with respect to \(B\) is defined as \[ \| \mathbf{v}\| := \sqrt{\left\langle \mathbf{v},\mathbf{v} \right\rangle} \,. \]
Two vectors \(\mathbf{v},\mathbf{w}\in V\) are orthogonal if \[ \left\langle \mathbf{v},\mathbf{w} \right\rangle = 0 \,. \]
Example 7
Proposition 8
Definition 9: Linear map
Remark 10: Matrix representation of linear maps
Definition 11: Eigenvalues and eigenvectors
Definition 12: Self-adjoint map
Theorem 13: Spectral Theorem
There is also a matrix version of the spectral theorem. To state it, we need to introduce some terminology.
Definition 14
Let \(A \in \mathbb{R}^{n \times n}\) be a matrix. We say that:
\(A\) is symmetric if \[ A^T = A \,. \]
\(A\) is orthogonal if \[ A^T A = I \,, \] where \(I\) is the identity matrix.
Remark 15
Let \(L \colon V \to V\) be linear and \(A \in \mathbb{R}^{n \times n}\) be the matrix associated to \(L\) with respect to any basis \(\{\mathbf{v}_1,\ldots,\mathbf{v}_n\}\) of \(V\). They are equivalent:
- \(L\) is self-adjoint,
- \(A\) is symmetric.
Definition 16: Matrix eigenvalues
Remark 17
Remark 18
Let \(L \colon V \to V\) be a linear map and \(A\) the associated matrix with respect to any basis of \(V\). Then \[ L(\mathbf{v}) = A \mathbf{x}\,, \quad \, \forall \, \mathbf{v}\in V\,, \] where \(\mathbf{x}\in \mathbb{R}^n\) is the vector of coordinates of \(\mathbf{v}\). They are equivalent:
- \(\lambda\) is an eigenvalue of \(L\) of eigenvector \(\mathbf{v}\),
- \(\lambda\) is an eigenvalue of \(A\) of eigenvector \(\mathbf{x}\).
Theorem 19: Spectral Theorem for matrices
Remark 20
4.1.2 Topology of \(\mathbb{R}^n\)
The Euclidean norm on \(\mathbb{R}^n\) is denoted by \[ \| \mathbf{x}\| := \sqrt{ \sum_{i=1}^n x_i^2 }\,, \quad \mathbf{x}= (x_1 , \ldots, x_n) \in \mathbb{R}^n \,. \] The Euclidean norm induces the distance \[ d(\mathbf{x},\mathbf{y}) := \| \mathbf{x}- \mathbf{y}\| = \sqrt{ \sum_{i=1}^n (x_i - y_i)^2 } \,. \]
Definition 21: Euclidean Topology
Definition 22: Open Sets
Definition 23: Closed Sets
Example 24
The \(n\)-dimensional unit sphere \[ \mathbb{S}^n = \{ \mathbf{x}\in \mathbb{R}^{n+1} \, \colon \,\| x \| = 1 \} \] is not open in \(\mathbb{R}^{n+1}\), since for any \(\mathbf{x}\in \mathbb{S}^n\) we have \[ B_{\varepsilon} (\mathbf{x}) \not\subseteq \mathbb{S}^{n} \,. \]
The \(n\)-dimensional unit cube \[ C := \{ \mathbf{x}\in \mathbb{R}^n \, \colon \,|x_1| + \ldots + |x_n| <1 \} \] is open in \(\mathbb{R}^n\), since one can always find \(\varepsilon>0\) small enough so that \[ B_{\varepsilon} (\mathbf{x}) \not\subseteq C \,. \]
The set \[ V := \{ \mathbf{x}\in \mathbb{R}^n \, \colon \,|x_1| + \ldots + |x_n| \geq 1 \} \] is closed, since \(V^c = C\) is the unit cube, which is open.
Definition 25: Subspace Topology
4.1.3 Smooth functions
We recall some basic facts about smooth functions from \(\mathbb{R}^n\) into \(\mathbb{R}^m\). For a vector valued function \(f \colon \mathbb{R}^n \to \mathbb{R}^m\) we denote its components by \[ f = (f_1,\ldots,f_m) \,. \]
Definition 26: Continuous Function
Remark 27
Definition 28: Homeomorphism
Definition 29: Differentiable Function
We denote by \(\{\mathbf{e}_i\}_{i=1}^n\) the standard basis of \(\mathbb{R}^n\).
Definition 30: Partial Derivative
Definition 31: Jacobian Matrix
Definition 32: Multi-index notation
Definition 33: Smooth Function
Notation: Gradient and partial derivatives
For \(f \colon U \subseteq \mathbb{R}^n \to \mathbb{R}\) smooth we denote the gradient by \[ \nabla f (\mathbf{x}) = \left( f_{x_1}(\mathbf{x}) , \ldots , f_{x_n}(\mathbf{x}) \right) \,. \]
Example 34
Definition 35: Diffeomorphism
We recall, without proof, the Inverse Function Theorem. Please note that in the statement the function \(f\) is defined from \(\mathbb{R}^n\) into \(\mathbb{R}^n\).
Theorem 36: Inverse Function Theorem
Warning
Non-vanishing Jacobian determinant is a necessary condition for being a diffeomorphism.
Proposition 37
Example 38
4.2 Definition of Surface
We give our main definition of surface in \(\mathbb{R}^3\).
Definition 39: Surface
Let \(\mathcal{S}\subseteq \mathbb{R}^3\) be a connected set. We say that \(\mathcal{S}\) is a surface if for every point \(\mathbf{p}\in \mathcal{S}\) there exist an open set \(U \subseteq \mathbb{R}^2\) and a smooth map \[ {\pmb{\sigma}}\colon U \to {\pmb{\sigma}}(U) \subseteq \mathcal{S}\, \] such that
- \(\mathbf{p}\in {\pmb{\sigma}}(U)\)
- \({\pmb{\sigma}}(U)\) is open in \(\mathcal{S}\)
- \({\pmb{\sigma}}\) is a homeomorphism between \(U\) and \({\pmb{\sigma}}(U)\)
Further:
- The homeomorphism \({\pmb{\sigma}}\) is called a surface chart at \(\mathbf{p}\).
- For each \(i \in I\) suppose to have a surface chart \[ {\pmb{\sigma}}_i \colon U_i \to {\pmb{\sigma}}(U_i) \subseteq \mathcal{S}\,. \] We say that the family \[ \mathcal{A} = \{ {\pmb{\sigma}}_i\}_{i \in I} \] is an atlas of \(\mathcal{S}\) if \[ \mathcal{S}= \bigcup_{i \in I} {\pmb{\sigma}}_i(U_i) \,. \]
Remark 40
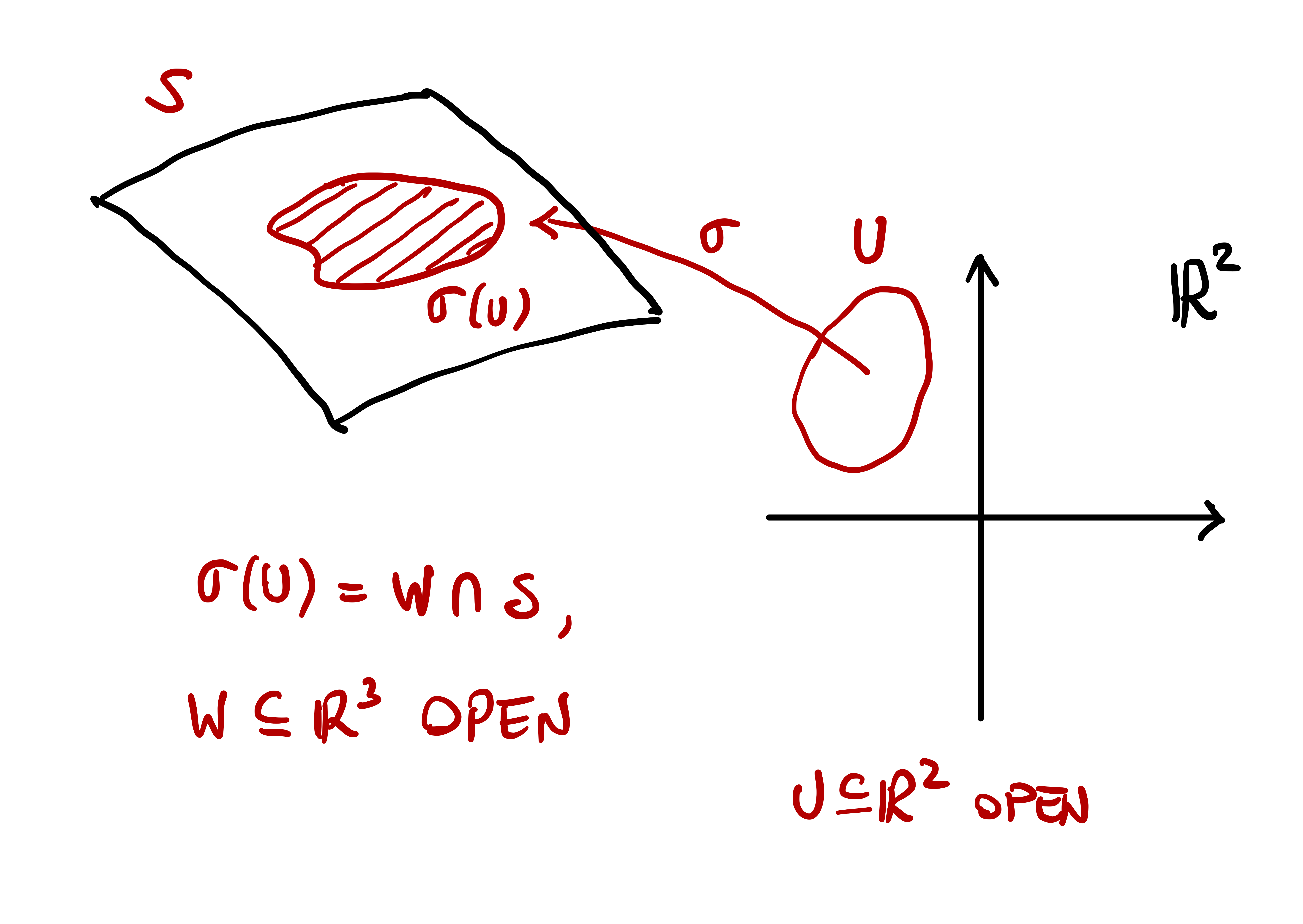
A surface chart \({\pmb{\sigma}}\) is a map \[ {\pmb{\sigma}}\colon U \to \mathbb{R}^3 \,, \] with \(U \subseteq \mathbb{R}^2\) open. Therefore smoothness of \({\pmb{\sigma}}\) is intended in the classical sense.
Given a chart \({\pmb{\sigma}}\colon U \to {\pmb{\sigma}}(U)\), the set \(U\) is open in \(\mathbb{R}^2\) while \({\pmb{\sigma}}(U)\) is open in \(\mathcal{S}\) with the subspace topology. This means that there exists \(W \subseteq \mathbb{R}^3\) open such that \[ {\pmb{\sigma}}(U) = W \cap \mathcal{S}\,. \]
The omeomorphism condition is saying that \({\pmb{\sigma}}(U) \subseteq \mathcal{S}\) looks locally (around \(\mathbf{p}\)) like an open set \(U \subseteq \mathbb{R}^2\).
Notation
Points in \(U\) will be denoted with the pair \((u,v)\).
Partial derivatives of a chart \({\pmb{\sigma}}= {\pmb{\sigma}}(u,v)\) will be denoted by \[ {\pmb{\sigma}}_u := \frac{\partial {\pmb{\sigma}}}{\partial u} \,, \quad {\pmb{\sigma}}_v := \frac{\partial {\pmb{\sigma}}}{\partial v} \,. \] Similar notations are adopted for higher order derivatives, e.g., \[\begin{align*} {\pmb{\sigma}}_{uu} & := \frac{\partial^2 {\pmb{\sigma}}}{\partial u^2} \,, & {\pmb{\sigma}}_{uv} & := \frac{\partial^2 {\pmb{\sigma}}}{\partial u \partial v} \,, \\ {\pmb{\sigma}}_{vu} & := \frac{\partial^2 {\pmb{\sigma}}}{\partial v \partial u } \,, & {\pmb{\sigma}}_{vv} & := \frac{\partial^2 {\pmb{\sigma}}}{\partial v^2 } \,, \\ \end{align*}\]
Components of \({\pmb{\sigma}}\) will be denoted by \[ {\pmb{\sigma}}= (\sigma^1, \sigma^2, \sigma^3) \,. \]
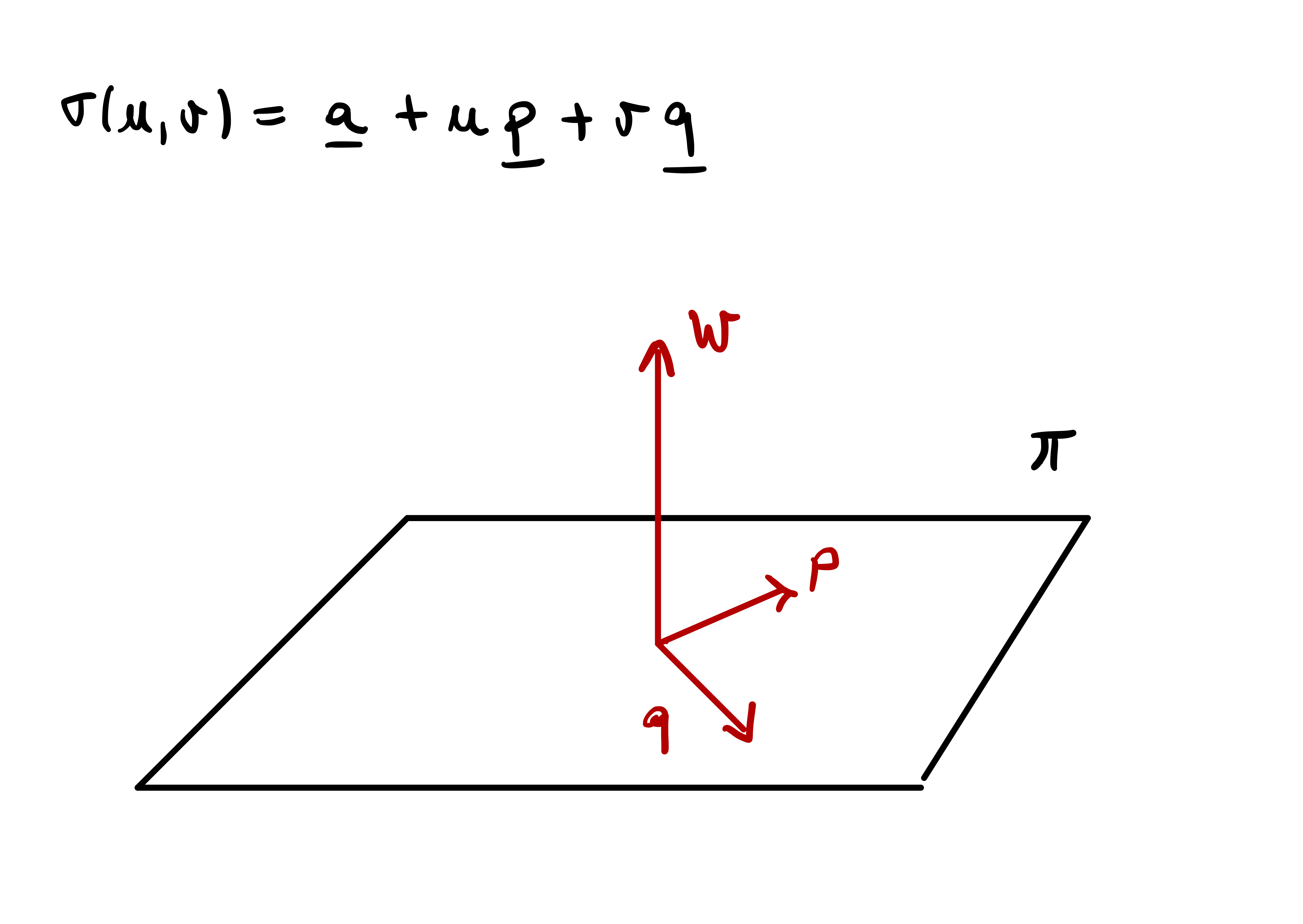
Example 41: 2D Plane in \(\mathbb{R}^3\)
- \(\mathbf{p},\mathbf{q} \in \mathbb{R}^3\) be ortoghonal to each other and to \(\mathbf{w}\).
- \(\mathbf{a} \in \pi\) be any point in the plane.
If \(\mathbf{x}\in \pi\) then \(\mathbf{x}-\mathbf{a}\) is parallel to the plane and \(\pi\) can be equivalently represented as \[ \pi = \{ \mathbf{a} + u \mathbf{p}+ v \mathbf{q} \, \colon \,u,v \in \mathbb{R}\} \,. \] Define the map \[ {\pmb{\sigma}}\colon \mathbb{R}^2 \to \pi \,, \quad {\pmb{\sigma}}(u,v):= \mathbf{a} + u \mathbf{p}+ v \mathbf{q} \,. \] We have:
- \({\pmb{\sigma}}\) is smooth.
- \(\mathbb{R}^2\) is obviously open.
- \({\pmb{\sigma}}(\mathbb{R}^2)\) is open in \(\pi\), since \({\pmb{\sigma}}(\mathbb{R}^2) = \pi\).
- The inverse of \({\pmb{\sigma}}\) is \[ {\pmb{\sigma}}^{-1} \colon \pi \to \mathbb{R}^2 \,, \quad {\pmb{\sigma}}^{-1} (\mathbf{x}) = ( (\mathbf{x}- \mathbf{a}) \cdot \mathbf{p}, (\mathbf{x}- \mathbf{a}) \cdot \mathbf{q} ) \,. \]
- As \({\pmb{\sigma}}^{-1}\) is continuous, then \({\pmb{\sigma}}\) is a homeomorphism between \(\mathbb{R}^2\) and \(\pi\).
Therefore \({\pmb{\sigma}}\) is a chart for \(\pi\). Since \[ {\pmb{\sigma}}(\mathbb{R}^2) = \pi \,, \] we have that \(\{{\pmb{\sigma}}\}\) is an atlas for \(\pi\), and hence \(\pi\) is a surface.
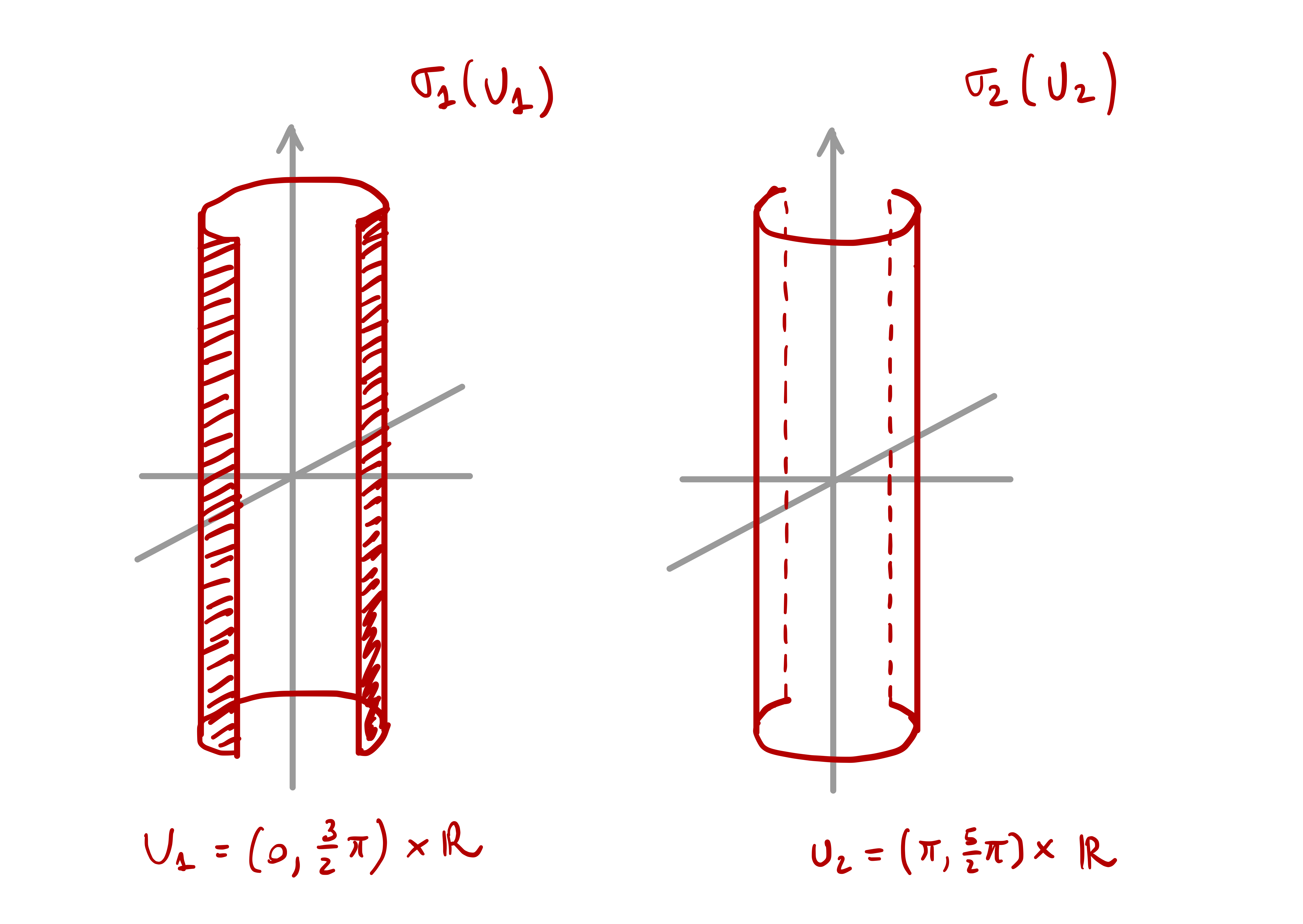
Example 42: Unit cylinder
Consider the infinite unit cylinder \[ \mathcal{S}= \{ (x,y,z) \in \mathbb{R}^3 \, \colon \,x^2 + y^2 = 1 \} \,. \] \(\mathcal{S}\) is a surface with an atlas consisting of two charts: \[ {\pmb{\sigma}}_i \colon U_i \to \mathbb{R}^3 \,, \quad {\pmb{\sigma}}_i(u,v):= (\cos(u),\sin(u),v) \] for \(i=1,2\), where \[ U_1 := \left( 0,\frac{ 3 \pi}{2} \right) \times \mathbb{R}\,, \quad U_2 := \left( \pi,\frac{ 5 \pi}{2} \right) \times \mathbb{R}\,. \]
Indeed:
- \({\pmb{\sigma}}_i\) is smooth.
- \(U_i\) is clearly open in \(\mathbb{R}^2\).
- One can check that \({\pmb{\sigma}}_i(U_i)\) is open in \(\mathcal{S}\).
- \({\pmb{\sigma}}_i\) is a homeomorphism of \(U_i\) in \({\pmb{\sigma}}(U_i)\).
- \(\{{\pmb{\sigma}}_1 , {\pmb{\sigma}}_2\}\) is an atlas for \(\mathcal{S}\), since \[ \mathcal{S}= {\pmb{\sigma}}_1(U_1) \cup {\pmb{\sigma}}_2(U_2) \,. \]
Important
Example 43: Graph of a function
Let \(U \subseteq \mathbb{R}^2\) be open and \(f \colon U \to \mathbb{R}\) be smooth. The graph of \(f\) is the set \[ \Gamma_f := \{ (u,v,f(u,v)) \, \colon \,(u,v) \in U \} \,. \] We have that \(\Gamma_f\) is a surface with atlas given by \[ \mathcal{A} = \{ {\pmb{\sigma}}\} \] where \({\pmb{\sigma}}\colon U \to \Gamma_f\) is \[ {\pmb{\sigma}}(u,v):=(u,v,f(u,v)) \,. \]
Let us check that \(\Gamma_f\) is a surface:
- \({\pmb{\sigma}}\) is smooth since \(f\) is smooth.
- \(U\) is open in \(\mathbb{R}^2\) by assumption.
- \({\pmb{\sigma}}(U) = \Gamma_f\), and therefore \({\pmb{\sigma}}(U)\) is open in \(\Gamma_f\).
- The inverse of \({\pmb{\sigma}}\) is given by \(\widetilde{{\pmb{\sigma}}} \colon \Gamma_f \to U\) defined as \[ \widetilde{{\pmb{\sigma}}}(u,v,f(u,v)) := (u,v) \,. \] Clearly \(\widetilde{{\pmb{\sigma}}}\) is continuous.
- Therefore \({\pmb{\sigma}}\) is a homeomorphism of \(U\) into \(\Gamma_f\).
- \(\mathcal{A}=\{{\pmb{\sigma}}\}\) is an atlas for \(\Gamma_f\), since \[ \Gamma_f = {\pmb{\sigma}}(U) \,. \]
Let us conclude the section with an example of a set which is not a surface.
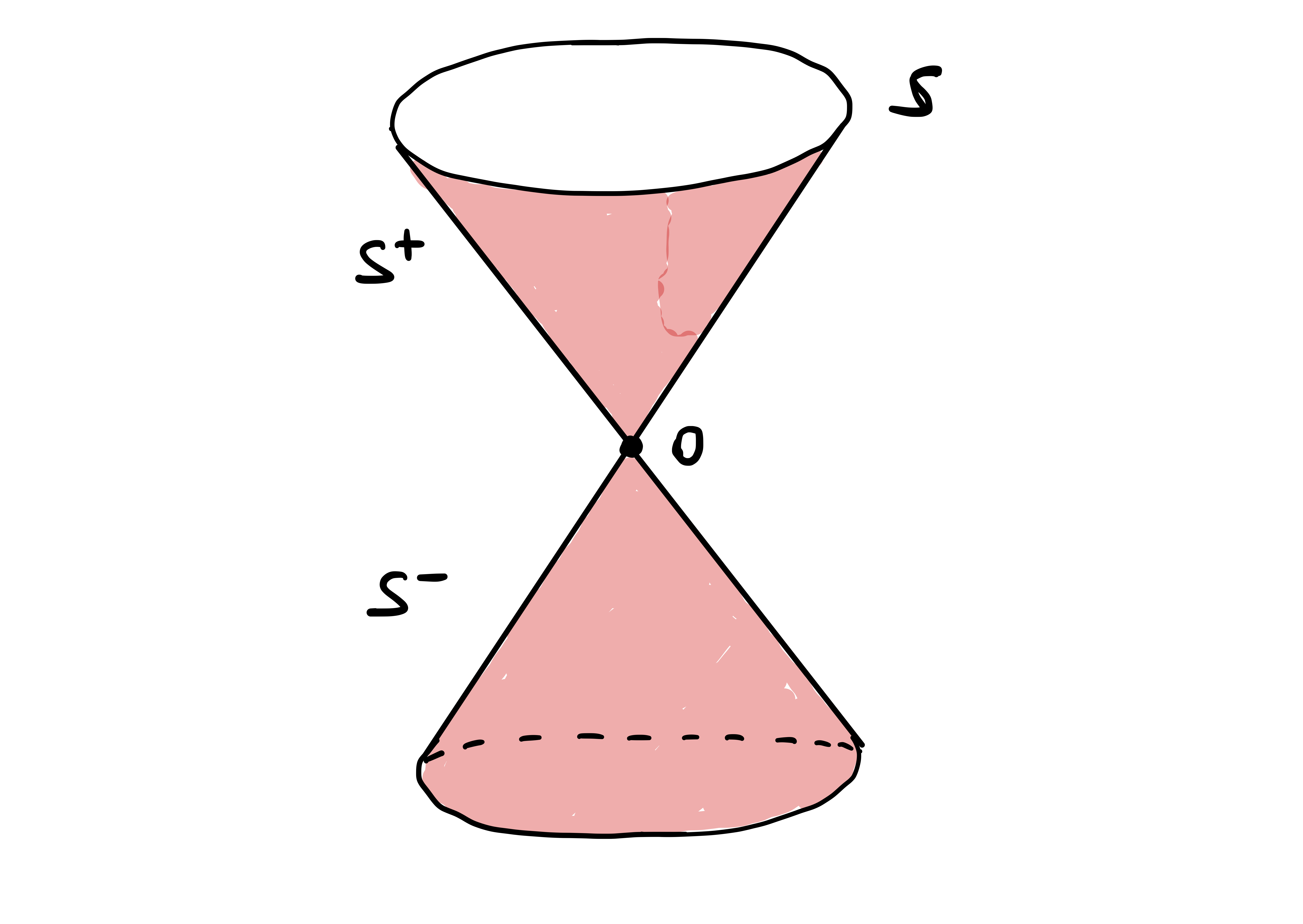
Example 44: Circular cone
To see that \(\mathcal{S}\) is not a surface, suppose there exists an atlas \(\{{\pmb{\sigma}}_i\}\) of \(\mathcal{S}\) \[ {\pmb{\sigma}}_i \colon U_i \to {\pmb{\sigma}}_i(U_i) \subseteq \mathcal{S}\,. \] In particular there exists a chart \({\pmb{\sigma}}\) such that \[ {\pmb{0}}\in {\pmb{\sigma}}(U) \,. \] Let \(\mathbf{x}_0 \in U\) be the point such that \[ {\pmb{\sigma}}(\mathbf{x}_0) = {\pmb{0}}\,. \] Since \(U\) is open in \(\mathbb{R}^2\), there exists \(\varepsilon>0\) such that \(B_{\varepsilon}(\mathbf{x}_0) \subseteq U\). Since \({\pmb{\sigma}}\) is a homeomorphism, we deduce that \[ {\pmb{\sigma}}(B_{\varepsilon}(\mathbf{x}_0)) \] is open in \(\mathcal{S}\). Hence there exists an open set \(W\) in \(\mathbb{R}^3\) such that \[ {\pmb{\sigma}}(B_{\varepsilon}(\mathbf{x}_0)) = {\pmb{\sigma}}(U) \cap W \,. \] As \({\pmb{0}}\in {\pmb{\sigma}}(B_{\varepsilon}(\mathbf{x}_0))\), we conclude that \({\pmb{0}}\in W\). Since \(W\) is open in \(\mathbb{R}^3\), there exists \(\delta > 0\) such that \[ B_{\delta} ({\pmb{0}}) \subseteq W \,. \] In particular we deduce that \[ B_{\delta} ({\pmb{0}}) \cap {\pmb{\sigma}}(U) \subseteq {\pmb{\sigma}}(B_{\varepsilon}(\mathbf{x}_0)) \,. \] Hence \({\pmb{\sigma}}(B_{\varepsilon}(\mathbf{x}_0))\) contains points of both \(\mathcal{S}^-\) and \(\mathcal{S}^+\), with \[ \mathcal{S}^- := \mathcal{S}\cap \{ z < 0 \} \,, \quad \mathcal{S}^+ := \mathcal{S}\cap \{ z > 0 \} \,. \] This implies that \[ V := {\pmb{\sigma}}(B_{\varepsilon}(\mathbf{x}_0)) \smallsetminus \{{\pmb{0}}\} \] is disconnected, with disconnection given by \[ V = ( V \cap \mathcal{S}^- ) \cup (V \cap \mathcal{S}^+) \,. \] However \(V\) is homeomorphic to \[ B_{\varepsilon} (\mathbf{x}_0) \smallsetminus \{ \mathbf{x}_0 \} \,, \] which is instead connected. Contradiction. Hence \(\mathcal{S}\) is not a surface.
4.3 Regular Surfaces
We have defined a regular curve to be a map \({\pmb{\gamma}}\colon (a,b) \to \mathbb{R}^n\) such that \[ \left\| {\pmb{\gamma}}(t) \right\| \neq 0 \,, \quad \forall \, t \in (a,b) \,. \] This allowed us to define tangent vectors and, eventually, Frenet frame.
We want to do something similar for surfaces: We look for a condition that eventually will allow us to define tangent planes. This is why we introduce regular charts and regular surfaces.
Definition 45: Regular Chart
The following gives more insight into the regularity condition.
Proposition 46
Let \(U \subseteq \mathbb{R}^2\) be open and consider a map \[ {\pmb{\sigma}}\colon U \to \mathbb{R}^3 \,. \] They are equivalent:
- \({\pmb{\sigma}}\) is a regular chart.
- The differential \(d{\pmb{\sigma}}_{\mathbf{x}} \colon \mathbb{R}^2 \to \mathbb{R}^3\) is injective for all \(\mathbf{x}\in U\).
- The Jacobian matrix \[ J{\pmb{\sigma}}(u,v) = \left( \begin{array}{ccc} \sigma^1_{u} & \sigma^1_{v} \\ \sigma^2_{u} & \sigma^2_{v} \\ \sigma^3_{u} & \sigma^3_{v} \\ \end{array} \right) \] has rank \(2\) for all \((u,v) \in U\).
- It holds \[ {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \neq 0 \, \quad \forall \, (u,v) \in U \,. \]
Proof
By the properties of vector product, we have that \[ {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \neq 0 \, \quad \, \forall (u,v) \in U \] if and only if \({\pmb{\sigma}}_u\) and \({\pmb{\sigma}}_v\) are linearly independent for all \((u,v) \in U\).
Part 2. Equivalence of Point 2 and Point 3.
The differential \(d{\pmb{\sigma}}_{\mathbf{x}} \colon \mathbb{R}^2 \to \mathbb{R}^3\) is represented in matrix form by the Jacobian \[ J{\pmb{\sigma}}(u,v) = \left( \begin{array}{ccc} \sigma^1_{u} & \sigma^1_{v} \\ \sigma^2_{u} & \sigma^2_{v} \\ \sigma^3_{u} & \sigma^3_{v} \\ \end{array} \right) \] By standard linear algebra results, \(J{\pmb{\sigma}}\) has rank 2 if and only if \(d{\pmb{\sigma}}\) is injective.
Part 3. Equivalence of Point 1 and Point 3.
A \(3 \times 2\) matrix has rank 2 if and only if its columns are linearly independent. Since the columns of \(J{\pmb{\sigma}}\) are \({\pmb{\sigma}}_u\) and \({\pmb{\sigma}}_v\), we conclude that \({\pmb{\sigma}}_u\) and \({\pmb{\sigma}}_v\) are linearly independent.
We are now ready to define regular surfaces.
Definition 47: Regular surface
Let \(\mathcal{S}\) be a surface. Let \[ \mathcal{A} = \{ {\pmb{\sigma}}_i \}_{i \in I} \,, \] be an atlas for \(\mathcal{S}\). We say that:
- \(\mathcal{A}\) is a regular atlas if the map \({\pmb{\sigma}}_i\) is a regular chart for all \(i \in I\).
- \(\mathcal{S}\) is a regular surface if there exists a regular atlas for \(\mathcal{S}\).
Example 48: 2D Plane in \(\mathbb{R}^3\)
Example 49: Unit cylinder
Example 50: Graph of a function
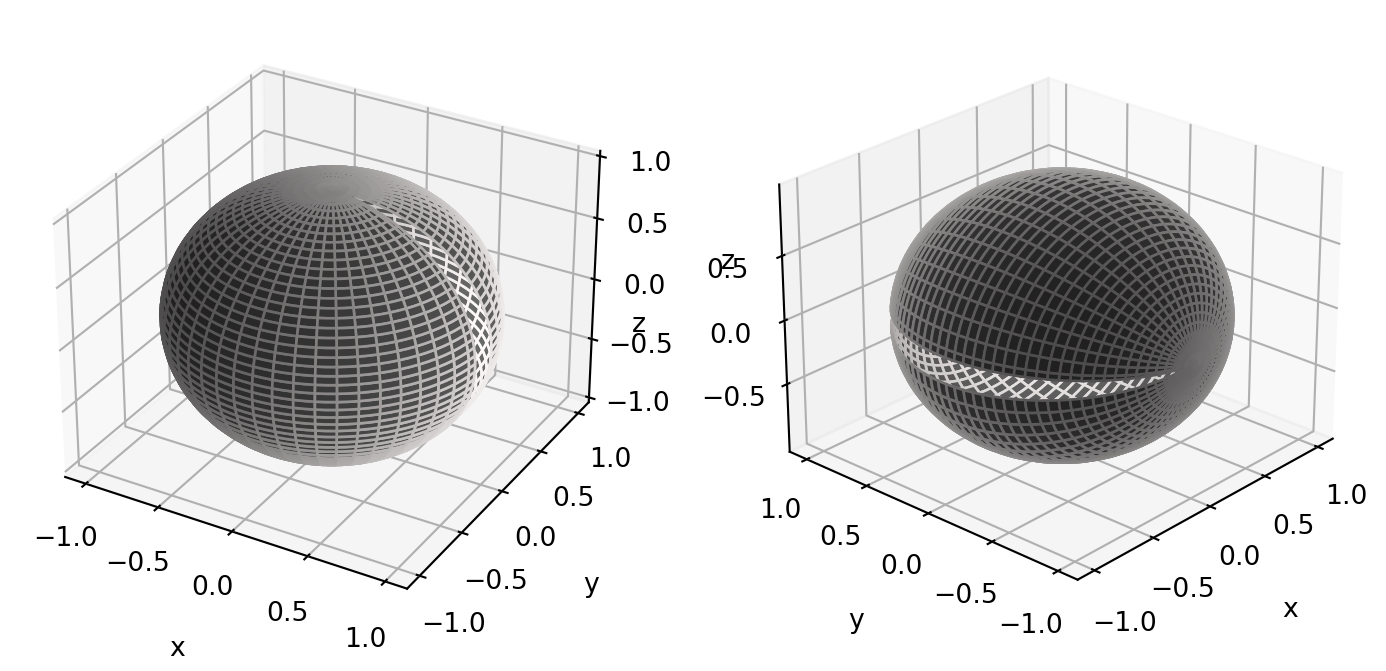
Example 51: Unit sphere
Consider the unit sphere in \(\mathbb{R}^3\) \[ \mathbb{S}^2 := \{ (x,y,z) \in \mathbb{R}^3 \, \colon \,x^2 + y^2 + z^2 = 1 \} \,. \] We have that \(\mathbb{S}^2\) is a regular surface, with regular atlas \[ \mathcal{A} = \{ {\pmb{\sigma}}_i \}_{i=1}^6 \,, \] defined as follows: Let \[ U:= \{ (u,v) \in \mathbb{R}^2 \colon u^2 + v^2 < 1 \} \] be the unit open ball in \(\mathbb{R}^2\) and define \({\pmb{\sigma}}_i \colon U \to \mathbb{R}^3\) by \[\begin{align*} {\pmb{\sigma}}_1 (u,v) & = \left(u,v,\sqrt{1-u^2-v^2} \right) \\ {\pmb{\sigma}}_2 (u,v) & = \left(u,v,-\sqrt{1-u^2-v^2} \right) \\ {\pmb{\sigma}}_3 (u,v) & = \left(u,\sqrt{1-u^2-v^2},v \right) \\ {\pmb{\sigma}}_4 (u,v) & = \left(u, -\sqrt{1-u^2-v^2}, v \right) \\ {\pmb{\sigma}}_5 (u,v) & = \left(\sqrt{1-u^2-v^2} , u ,v \right) \\ {\pmb{\sigma}}_6 (u,v) & = \left(-\sqrt{1-u^2-v^2}, u,v, \right) \\ \end{align*}\]
Exercise: Check that \(\mathbb{S}^2\) is a regular surface.
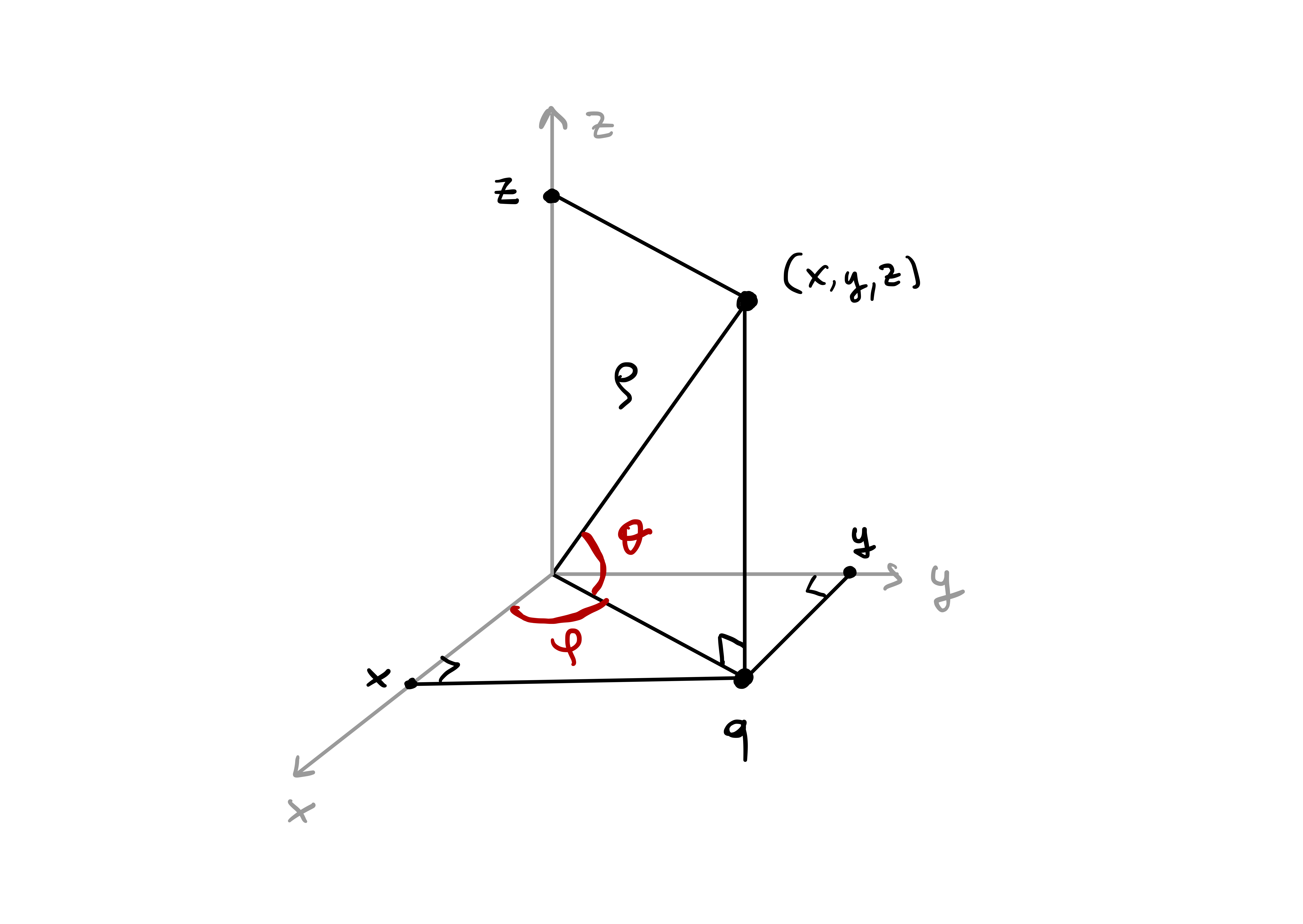
Remark 52: Spherical coordinates
The equivalent of polar coordinates in dimension \(3\) are spherical coordinates. A point \((x,y,z) \in \mathbb{R}^3 \smallsetminus \{{\pmb{0}}\}\) can be represented in spherical coordinates by \[\begin{align*} x & = \rho \cos (\theta) \cos(\phi) \\ y & = \rho \cos (\theta) \sin(\phi) \\ z & = \rho \sin (\theta) \end{align*}\] where \[ \rho:=\sqrt{ x^2 + y^2 + z^2 } \,, \quad \phi\in [0,2\pi] \,, \quad \theta \in \left[ -\frac{\pi}{2}, \frac{\pi}{2} \right] \,, \] with the angles \(\phi\) and \(\theta\) as in Figure Figure 4.1.
It is clear that \(z = \rho \sin(\theta)\), by basic trigonometry. To compute \(x\) and \(y\), we note that the segment joining \({\pmb{0}}\) to \(\mathbf{p}\) has length \[ L = \rho \cos \theta \,. \] Therefore we get \[\begin{align*} x & = L \cos (\phi) = \rho \cos (\theta) \cos(\phi) \\ y & = L \sin (\phi) = \rho \cos (\theta) \sin(\phi) \end{align*}\] concluding.
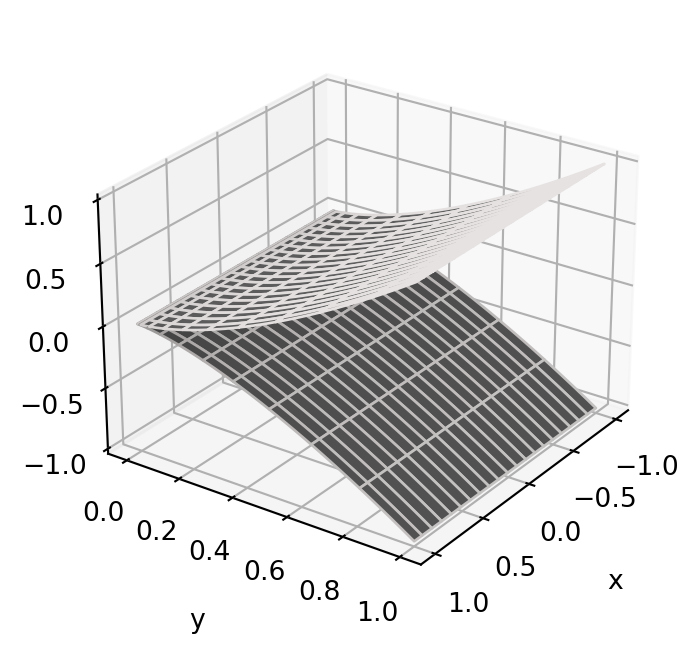
Example 53: Unit sphere in spherical coordinates
\({\pmb{\sigma}}\) is smooth.
\(U\) is open in \(\mathbb{R}^2\).
Moreover \[ {\pmb{\sigma}}(U) = \mathbb{S}^2 \smallsetminus \{ (x,0,z) \in \mathbb{R}^3 \, \colon \,x \geq 0 \} \,, \] as seen also in the left picture in Figure 4.2.
The set \({\pmb{\sigma}}(U)\) is evidently open in \(\mathbb{S}^2\).
It is easy to check that \({\pmb{\sigma}}\) is invertible, with continuous inverse.
Thus \({\pmb{\sigma}}\) is a homeomorphism from \(U\) into \({\pmb{\sigma}}(U)\).
Let us check that \({\pmb{\sigma}}\) is a regular chart: \[\begin{align*} {\pmb{\sigma}}_{\theta} & = (-\sin(\theta) \cos(\phi), -\sin(\theta) \sin(\phi), \cos(\theta) ) \\ {\pmb{\sigma}}_{\phi} & = ( - \cos(\theta) \sin(\phi), \cos(\theta) \cos(\phi), 0 ) \,. \end{align*}\] Therefore \[ {\pmb{\sigma}}_{\theta} \times {\pmb{\sigma}}_{\phi} = ( - \cos^2(\theta) \cos(\phi), - \cos^2(\theta) \sin(\phi), - \sin(\theta) \cos ( \theta ) ) \,, \] from which \[ \left\| {\pmb{\sigma}}_{\theta} \times {\pmb{\sigma}}_{\phi} \right\| = |\cos (\theta)| \, . \] Since \((\theta,\phi)\in U\), we have \(\theta \in ( -\pi/2, \pi/2 )\), and so \[ \left\| {\pmb{\sigma}}_{\theta} \times {\pmb{\sigma}}_{\phi} \right\| = |\cos (\theta)| \neq 0 \,, \] showing that \({\pmb{\sigma}}_{\theta}\) and \({\pmb{\sigma}}_{\phi}\) are linearly independent, and \({\pmb{\sigma}}\) is regular.
Since \({\pmb{\sigma}}(U) \neq \mathbb{S}^2\), the chart \({\pmb{\sigma}}\) does not form an atlas. We need a second chart. An option is to define \(\widetilde{{\pmb{\sigma}}} \colon U \to \mathbb{R}^3\) by \[ \widetilde{{\pmb{\sigma}}} := ( - \cos(\theta) \cos (\phi), -\sin(\theta) , - \cos (\theta) \sin(\phi)) \,. \] Notice that \(\widetilde{{\pmb{\sigma}}}\) is obtained by rotating \({\pmb{\sigma}}\) by \(\pi\) about the \(z\)-axis and by \(\pi/2\) about the \(y\)-axis, as seen in the right picture in Figure 4.2. It is an exercise to check that \(\widetilde{{\pmb{\sigma}}}\) is a regular chart.
Since we have \[ \widetilde{{\pmb{\sigma}}} (U) = \mathbb{S}^2 \smallsetminus \{ (x,y,0) \in \mathbb{R}^3 \, \colon \,x \leq 0 \} \,, \] it is immediate to see that \[ \mathbb{S}^2 = {\pmb{\sigma}}(U) \cup \widetilde{{\pmb{\sigma}}}(U) \,. \] Hence \[ \mathcal{A} := \{ {\pmb{\sigma}}, \widetilde{{\pmb{\sigma}}} \} \] is a regular atlas for \(\mathbb{S}^2\).
Let us make an example of a non-regular surface.
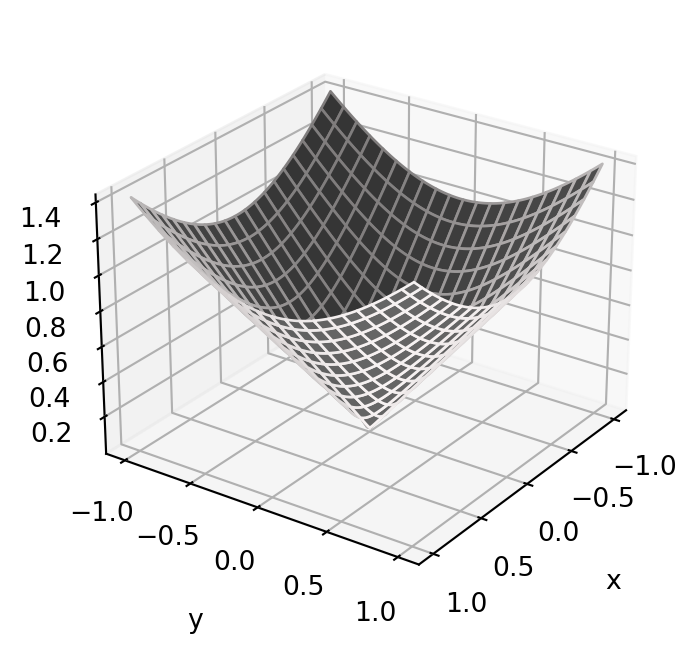
Example 54
Looking at Figure Figure 4.3, it is clear that \(\mathcal{S}\) is not regular, since \(\mathcal{S}\) has a cusp along the line \({\pmb{\sigma}}(L)\).
4.4 Level surfaces
Definition 55: Level surface
We now give a result concerning regularity of level surfaces. The proof, rather technical, is based on the Implicit Function Theorem and can be found in Proposition 3.1.25 of (Abate, Marco and Tovena, Francesca 2011). We decide to omit it.
Theorem 56
Example 57
Let us prove that \(\mathcal{S}\) is regular by using Theorem 56. To this end, define the open set \[ V := \mathbb{R}^3 \smallsetminus \{ (0,0,z) \, \colon \,z \in \mathbb{R}\} \,. \] Note that \(V\) is obtained by removing the \(z\)-axis from \(\mathbb{R}^3\). Also define the function \(f \colon \mathbb{R}^3 \to \mathbb{R}\) by \[ f(x,y,z) := x^2 + y^2 -1 \,. \] We have \[ \nabla f (x,y,z) = ( 2x, 2y, 0 ) \neq 0 \,, \quad \forall \, (x,y,z) \in V \,. \] Since \[ \mathcal{S}= \mathcal{S}_f \,, \] by Theorem 56 we conclude that \(\mathcal{S}\) is a regular surface.
Example 58: Circular cone
As a side note, a regular atlas for \(\mathcal{S}^+\) is given by \(\mathcal{A} = \{{\pmb{\sigma}}\}\) where \({\pmb{\sigma}}\colon \mathbb{R}^2 \to \mathbb{R}^3\) is defined by \[ {\pmb{\sigma}}(u,v) := (u,v,\sqrt{u^2 + v^2}) \,. \]
4.5 Reparametrizations
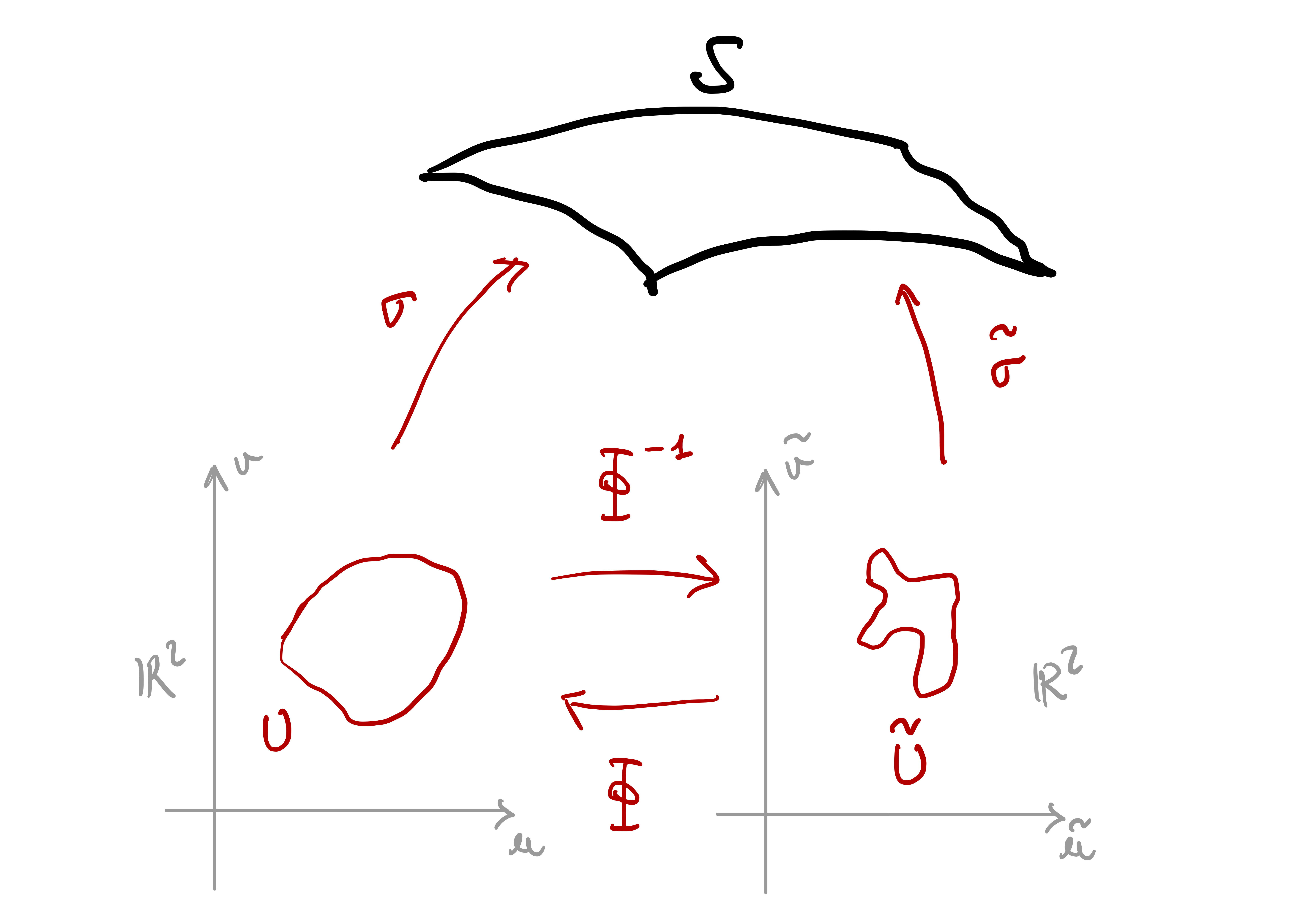
We have defined the reparametrization of curves. In a similar way, one can reparametrize surface charts.
Definition 59
We will show that reparametrizations of regular charts are regular. To prove this, first we need to recall the chain rule for multivariable functions.
Remark 60: Chain rule
The chain rule states that \[ J \tilde{f} (\tilde u, \tilde v) = Jf ( \Phi (\tilde u, \tilde v) ) \, J\Phi (\tilde u, \tilde v) \,. \] By expanding the above identity we obtain the chain rule in vectorial form \[\begin{align*} \tilde{f}_{\tilde{u}} (\tilde{u}, \tilde{v}) & = f_u ( \Phi(\tilde{u}, \tilde{v}) ) \Phi_{\tilde{u}}^1 (\tilde{u}, \tilde{v}) + f_v ( \Phi(\tilde{u}, \tilde{v}) ) \Phi_{\tilde{u}}^2 (\tilde{u}, \tilde{v}) \\ \tilde{f}_{\tilde{v}} (\tilde{u}, \tilde{v}) & = f_u ( \Phi(\tilde{u}, \tilde{v}) ) \Phi_{\tilde{v}}^1 (\tilde{u}, \tilde{v}) + f_v ( \Phi(\tilde{u}, \tilde{v}) ) \Phi_{\tilde{v}}^2 (\tilde{u}, \tilde{v}) \end{align*}\] As done previously, we introduce compact notation for reparametrizations and chain rule. Specifically, we denote the components of the diffeomorphism \(\Phi\) by \[\begin{align*} \Phi^1 \quad & \leadsto \quad (\tilde u, \tilde v) \mapsto u (\tilde u, \tilde v) \\ \Phi^2 \quad & \leadsto \quad (\tilde u, \tilde v) \mapsto v (\tilde u, \tilde v) \end{align*}\] Accordingly, the Jacobian of \(\Phi\) is denoted as: \[ J \Phi = \left( \begin{array}{cc} {\Phi}^1_{\tilde u} & {\Phi}^1_{\tilde v} \\ {\Phi}^2_{\tilde u} & {\Phi}^2_{\tilde v} \end{array} \right) \quad \leadsto \quad \left( \begin{array}{cc} \dfrac{\partial u}{\partial \tilde u} & \dfrac{\partial u}{\partial \tilde v} \\ \dfrac{\partial v}{\partial \tilde u} & \dfrac{\partial v}{\partial \tilde v} \end{array} \right) \,. \] Hence, the chain rule in vectorial form reads \[\begin{align*} \tilde{f}_{\tilde{u}} & = f_u \frac{\partial u}{\partial \tilde{u}} + f_v \frac{\partial v}{\partial \tilde{u}} \\ \tilde{f}_{\tilde{v}} & = f_u \, \frac{\partial u}{\partial \tilde{v}} + f_v \frac{\partial v}{\partial \tilde{v}} \end{align*}\]
We will now prove that the reparametrization of a regular chart is regular.
Proposition 61
Proof
4.6 Transition maps
Consider the situation in which two regular charts have overlapping image.
It is natural to ask wether these maps are reparametrizations of each other on the overlapping region, see Figure 4.5. If such reparametrization exists, it is called a transition map.
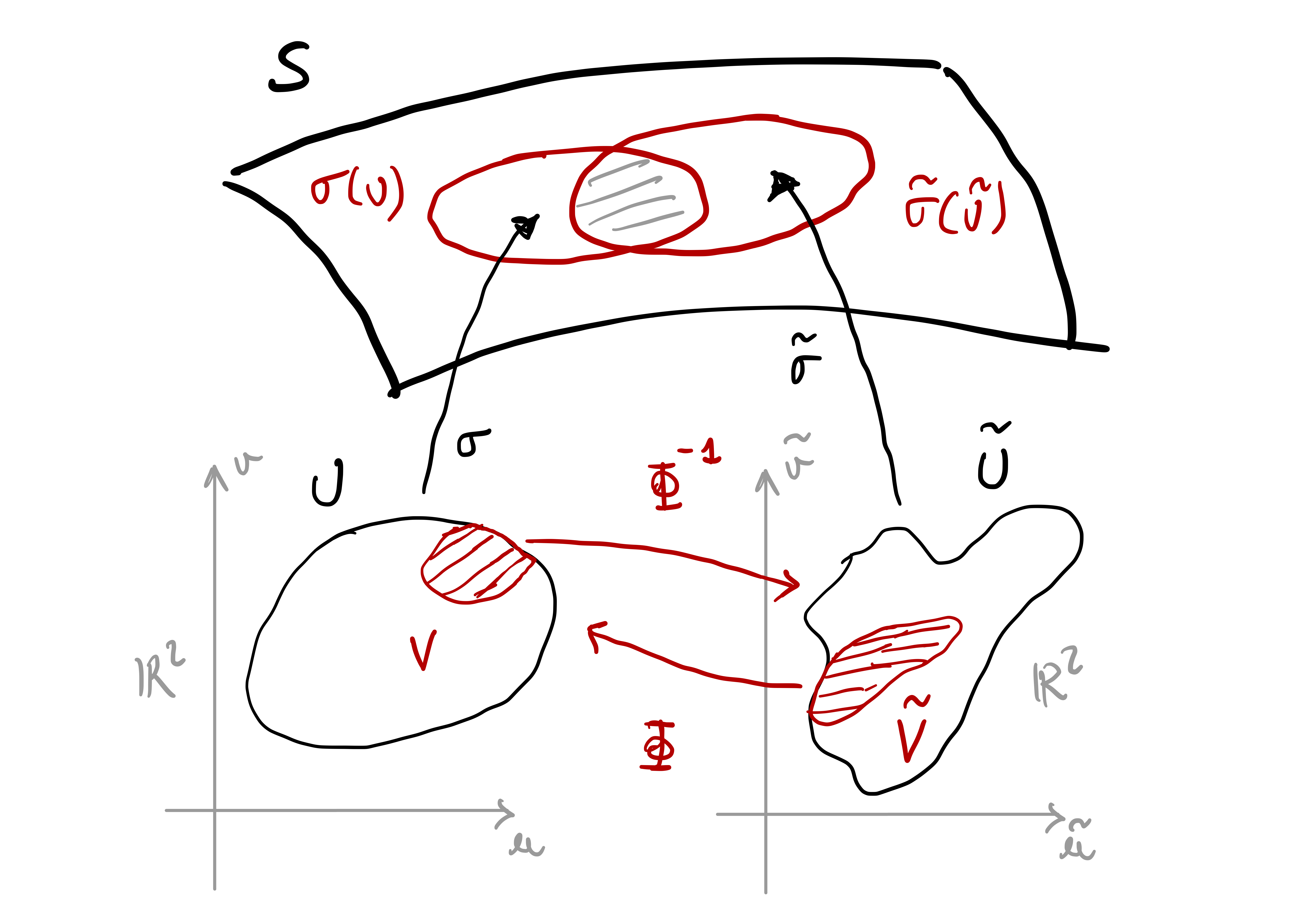
Definition 62: Transition map
The theorem below states that transition maps between regular charts are diffeomorphisms. The proof is slightly technical and is based on the Implicit Function Theorem. We decide to omit it. The interested reader can find a proof at Page 117 of (Pressley 2010).
Theorem 63
We can now use Theorem 63 to show that transition maps are reparametrizations.
Proposition 64
Proof
Important
4.7 Functions between surfaces
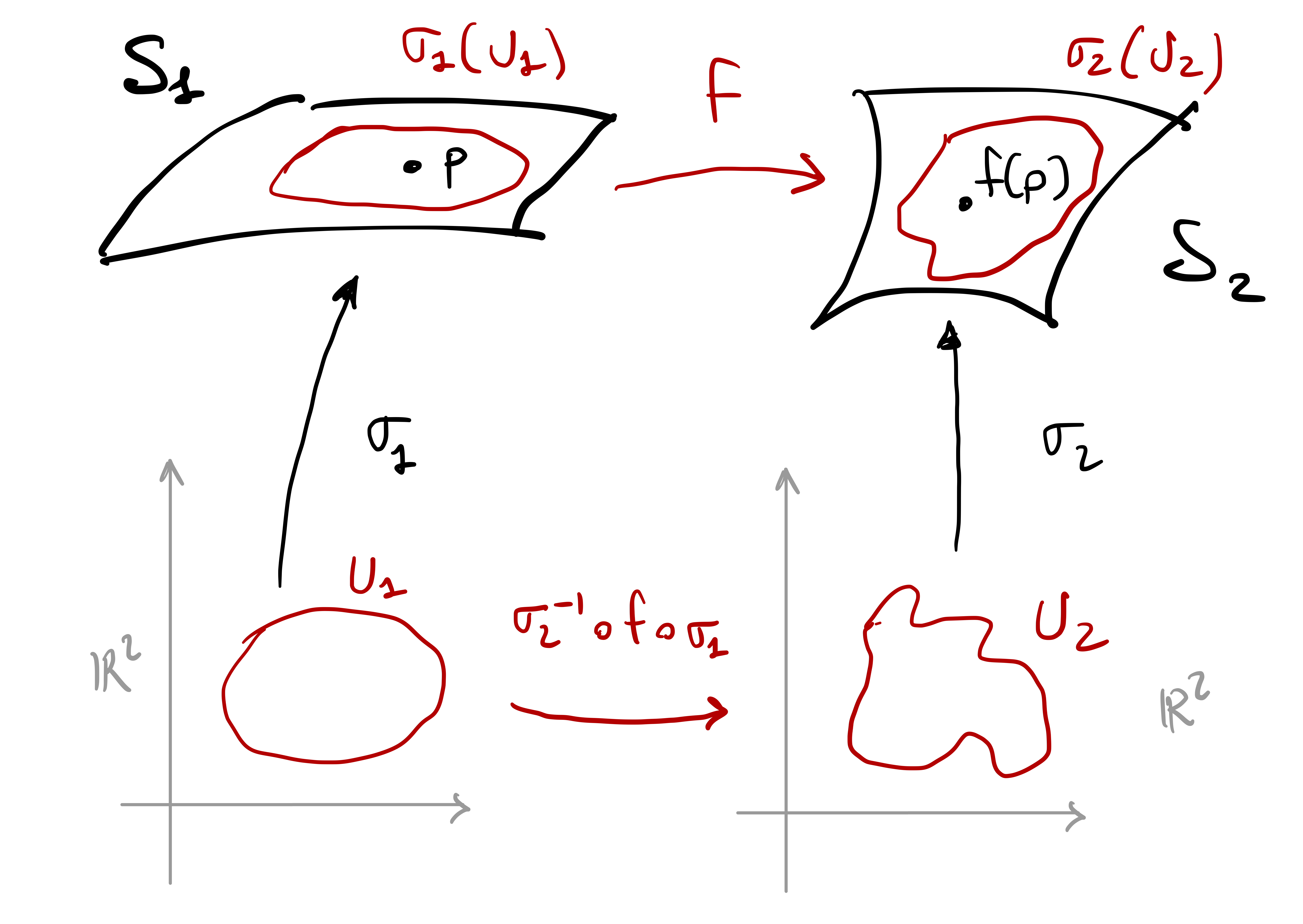
We would like to define a concept of smooth function \[ f \colon \mathcal{S}_1 \to \mathcal{S}_2 \,, \] where \(\mathcal{S}_1\) and \(\mathcal{S}_2\) are regular surfaces. So far we know what a smooth function from \(\mathbb{R}^n\) into \(\mathbb{R}^m\) is. The idea is to use surface charts to define such \(f\).
Definition 65
Let \(\mathcal{S}_1\) and \(\mathcal{S}_2\) be regular surfaces and let \[ f \colon \mathcal{S}_1 \to \mathcal{S}_2 \] be a map. We say that:
\(f\) is smooth at \(\mathbf{p}\in \mathcal{S}_1\) if there exist charts \({\pmb{\sigma}}_i \colon U_i \to \mathcal{S}_i\) for \(i=1,2\) such that \[ \mathbf{p}\in {\pmb{\sigma}}_1(U_1)\,, \quad f(\mathbf{p}) \in {\pmb{\sigma}}_2(U_2) \] and \[ ({\pmb{\sigma}}_2^{-1} \circ f \circ {\pmb{\sigma}}_1 ) \colon U_1 \to U_2 \] is smooth.
\(f\) is smooth if it is smooth for each \(\mathbf{p}\in \mathcal{S}_1\).
\(f\) is a diffeomorphism if \(f\) is smooth and invertible, with smooth inverse.
Remark 66
Definition 65 makes sense because \({\pmb{\sigma}}_2^{-1}\) exists.
The map \({\pmb{\sigma}}_2^{-1} \circ f \circ {\pmb{\sigma}}_1\) is only defined for \(\mathbf{x}\in U_1\) such that \[ f ( {\pmb{\sigma}}_1 (\mathbf{x}) ) \in {\pmb{\sigma}}_2 (U_2) \,. \]
The function \({\pmb{\sigma}}_2^{-1} \circ f \circ {\pmb{\sigma}}_1\) maps from \(\mathbb{R}^2\) into \(\mathbb{R}^2\), therefore differentiability is intended in the classical sense.
Definition 65 does not depend on the choice of charts \({\pmb{\sigma}}_1\) and \({\pmb{\sigma}}_2\)
Indeed, suppose that \(\widetilde{{\pmb{\sigma}}}_{i} \colon \widetilde{U}_i \to {\mathcal{S}}_i\) are charts such that \[ \mathbf{p}\in \widetilde{{\pmb{\sigma}}}_1( \widetilde{U}_1) \,, \quad f(\mathbf{p}) \in \widetilde{{\pmb{\sigma}}}_2(\widetilde{U}_2) \,. \] In particular we have \[ {\pmb{\sigma}}_i(U_i) \cap \widetilde{{\pmb{\sigma}}}_i (\widetilde{U}_i) \neq \emptyset \,. \] As \(\mathcal{S}_1\) and \(\mathcal{S}_2\) are regular surfaces, by Theorem 63 there exist open sets \[ V_i \subseteq U_i \,, \quad \widetilde{V}_i \subseteq \widetilde{U}_i \,, \] and transition maps \[ \Phi_i \colon \widetilde{V}_i \to V_i \] which are diffeomorphisms and satisfy \[ \widetilde{{\pmb{\sigma}}}_i = {\pmb{\sigma}}_i \circ \Phi_i \,. \] Hence \[\begin{align*} \widetilde{{\pmb{\sigma}}}_2^{-1} \circ f \circ \widetilde{{\pmb{\sigma}}}_1 & = \widetilde{{\pmb{\sigma}}}_2^{-1} \circ ( {\pmb{\sigma}}_2 \circ {\pmb{\sigma}}_2^{-1} ) \circ f \circ ( {\pmb{\sigma}}_1 \circ {\pmb{\sigma}}_1^{-1} ) \circ \widetilde{{\pmb{\sigma}}}_1 \\ & = ( \widetilde{{\pmb{\sigma}}}_2^{-1} \circ {\pmb{\sigma}}_2 ) \circ ( {\pmb{\sigma}}_2^{-1} \circ f \circ {\pmb{\sigma}}_1 ) \circ ({\pmb{\sigma}}_1^{-1} \circ \widetilde{{\pmb{\sigma}}}_1 ) \\ & = \Phi_2^{-1} \circ ( {\pmb{\sigma}}_2^{-1} \circ f \circ {\pmb{\sigma}}_1 ) \circ \Phi_1^{-1} \,. \end{align*}\] Since \(\Phi_i^{-1}\) and \({\pmb{\sigma}}_2^{-1} \circ f \circ {\pmb{\sigma}}_1\) are smooth, we conclude that \[ \widetilde{{\pmb{\sigma}}}_2^{-1} \circ f \circ \widetilde{{\pmb{\sigma}}}_1 \] is smooth. Hence Definition 65 does not depend on the choice of charts.
Proposition 67
Proof
Definition 68
The key ideas around diffeomorphisms are:
Two diffeomorphic surfaces are essentially the same. Indeed, it is immediate to show that being diffeomorphic is an equivalence relation on the set of regular surfaces.
Two diffeomorphic surfaces have essentially the same charts, as shown in the next proposition.
Proposition 69
Proof
We conclude with the definition of local diffeomorphism between surfaces.
Definition 70: Local diffeomorphism
The above definition is well posed since open subsets of surfaces are themselves surfaces.
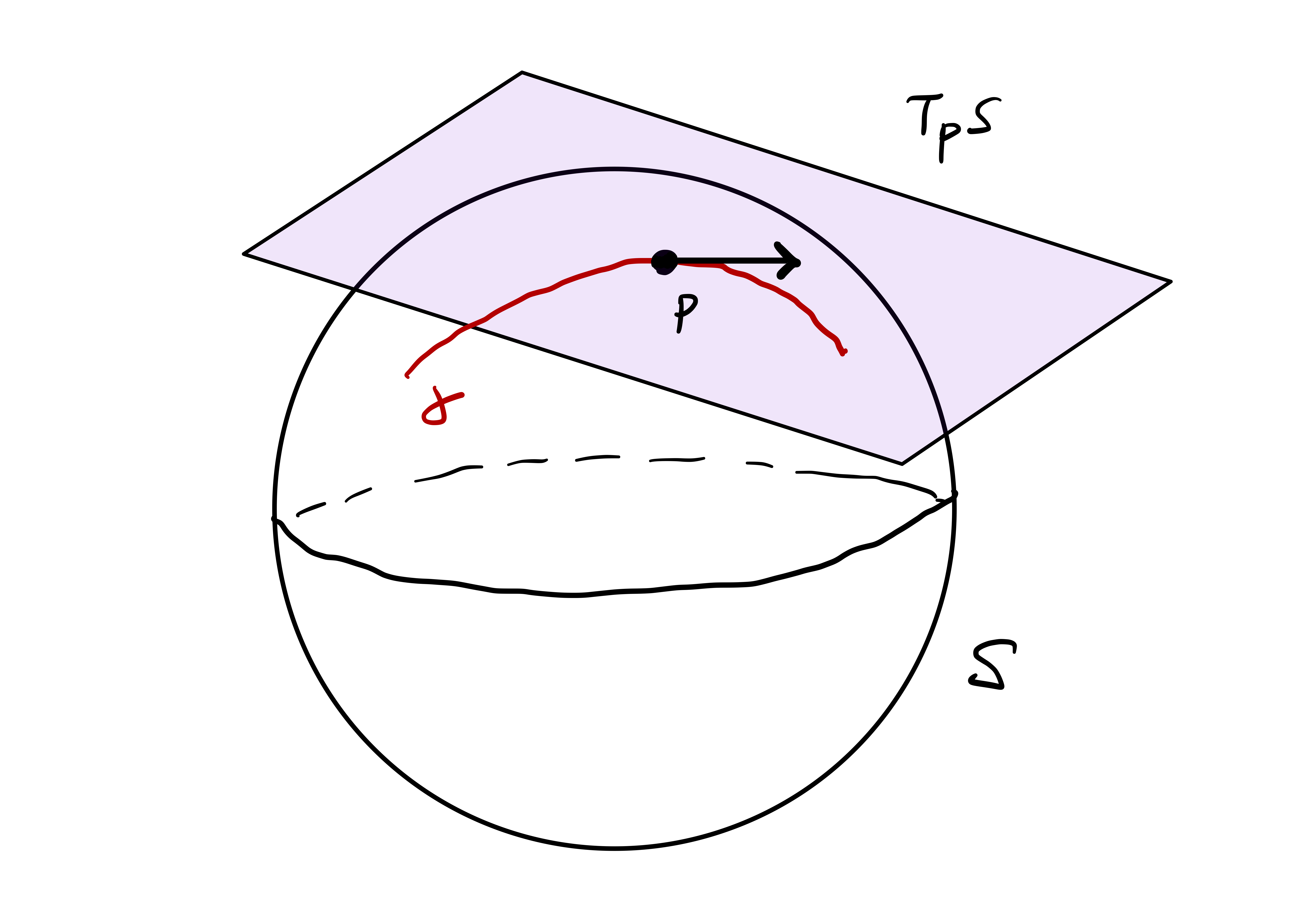
4.8 Tangent space
We have seen that tangent vectors to regular curves allow to define the Frenet Frame, curvature and torsion. Eventually, these quantities are sufficient to characterize a curve. The anolgue concept of tangent vector for surfaces is called the tangent space. To avoid clumsy terminology, we make the following assumption.
Assumption 71
Definition 72: Tangent vectors and tangent space
Let us start with the most basic example: We want to compute the tangent space to an open set in \(\mathbb{R}^2\).
Example 73
Let \(U \subseteq \mathbb{R}^2\) be open and \(\mathbf{p}\in U\). Then \[ T_{\mathbf{p}} U = \mathbb{R}^2 \,. \]
Proof. Let \(\mathbf{v}\in T_{\mathbf{p}} U\). By definition there exists a smooth curve \[ \gamma \colon (-\varepsilon,\varepsilon) \to U \] such that \({\pmb{\gamma}}(0) = \mathbf{p}\) and \(\dot{{\pmb{\gamma}}}(0)=\mathbf{v}\). Since \(U \subseteq \mathbb{R}^2\), it follows that \({\pmb{\gamma}}\) is a plane curve, so that \[ \mathbf{v}= \dot{{\pmb{\gamma}}}(0) \in \mathbb{R}^2 \,. \] Conversely, let \(\mathbf{v}\in \mathbb{R}^2\). Since \(\mathbf{p}\in U\) and \(U\) is open, there exists \(\varepsilon>0\) such that \(B_{\varepsilon}(p) \subseteq U\). Define the curve \[ {\pmb{\gamma}}\colon (-\varepsilon,\varepsilon) \to \mathbb{R}^3 \,, \quad {\pmb{\gamma}}(t):= \mathbf{p}+ t \mathbf{v}\,. \] By construction \[ {\pmb{\gamma}}(-\varepsilon,\varepsilon) \subseteq B_{\varepsilon} (\mathbf{p}) \subseteq U \,, \quad {\pmb{\gamma}}(0) = \mathbf{p}\,, \quad \dot{{\pmb{\gamma}}}(0)= \mathbf{v}\,, \] showing that \(\mathbf{v}\in T_{\mathbf{p}} U\).
In the above example we have seen that \(T_{\mathbf{p}} U = \mathbb{R}^2\). This property holds in general for \(T_{\mathbf{p}} \mathcal{S}\) with \(\mathcal{S}\) regular surface. Before proving this fact, we need a lemma.
Lemma 74
Let \(\mathcal{S}\) be regular and \(\mathbf{p}\in \mathcal{S}\). Let \({\pmb{\sigma}}\colon U \to {\pmb{\sigma}}(U) \subseteq \mathcal{S}\) be a regular chart at \(\mathbf{p}\), with \[ {\pmb{\sigma}}(u_0,v_0) = \mathbf{p}\,. \] We have:
Suppose \({\pmb{\gamma}}\colon (-\varepsilon,\varepsilon) \to \mathbb{R}^3\) is a smooth curve such that \[ {\pmb{\gamma}}(-\varepsilon,\varepsilon) \subseteq {\pmb{\sigma}}(U) \,, \quad {\pmb{\gamma}}(0) = \mathbf{p}\,. \] Then there exist smooth functions \[ u , v \colon (-\varepsilon,\varepsilon) \to \mathbb{R} \] such that \[ {\pmb{\gamma}}(t) = {\pmb{\sigma}}( u(t), v(t) ) \,, \quad \forall \, t \in (-\varepsilon,\varepsilon) \,, \] and \[ u(0)=u_0 \,, \quad v(0) = v_0 \,. \]
Conversely, assume \(u , v \colon (-\varepsilon,\varepsilon) \to \mathbb{R}\) are smooth functions such that \[ u(0)=u_0 \,, \quad v(0) = v_0 \,. \] Then \[ {\pmb{\gamma}}(t):= {\pmb{\sigma}}(u(t),v(t)) \] is a smooth curve such that \[ {\pmb{\gamma}}(-\varepsilon,\varepsilon) \subseteq \mathcal{S}\,, \quad {\pmb{\gamma}}(0)=\mathbf{p}\,. \]
Proof
- \(W \subseteq U \subseteq \mathbb{R}^2\) open set with \((u_0,v_0) \in W\),
- \(V \subseteq \mathbb{R}^2\) open set with \(F(u_0,v_0) \in V\),
such that \[ F \colon W \to V \] is a diffeomorphism. Hence \[ F^{-1} \colon V \to W \] is smooth. Since \({\pmb{\gamma}}(-\varepsilon,\varepsilon) \subseteq {\pmb{\sigma}}(U)\), it is well defined the composition \[ F^{-1} \circ {\pmb{\gamma}}\colon (-\varepsilon,\varepsilon) \to W \subseteq U \,. \] Moreover such composition is smooth, being \(F^{-1}\) and \({\pmb{\gamma}}\) smooth. Therefore \[ (F^{-1} \circ {\pmb{\gamma}}) (t) = (u(t),v(t)) \tag{4.2}\] with \(u,v\) smooth. As \({\pmb{\gamma}}(0)=\mathbf{p}\), by definition of \(F\) we have \[ (u(0),v(0)) = (F^{-1} \circ {\pmb{\gamma}}) (0) = F^{-1}(\mathbf{p}) = (u_0,v_0) \,, \] showing that \[ u(0) = u_0 \,, \quad v(0) = v_0 \,. \] Moreover, applying \({\pmb{\sigma}}\) to both sides of (4.2) yields \[ {\pmb{\sigma}}(u(t),v(t)) = {\pmb{\sigma}}((F^{-1} \circ {\pmb{\gamma}})) (t) = {\pmb{\gamma}}(t) \,, \] as we wanted to show.
The converse statement is trivial.
We are now ready to characterize \(T_{\mathbf{p}} \mathcal{S}\) when \(\mathcal{S}\) is a regular surface.
Theorem 75
Proof
Step 1. Suppose \(\mathbf{v}\in T_{\mathbf{p}} \mathcal{S}\). By definition there exists a smooth curve \({\pmb{\gamma}}\colon (-\varepsilon,\varepsilon) \to \mathcal{S}\) such that \[ {\pmb{\gamma}}(0) = \mathbf{p}\,, \quad \dot{{\pmb{\gamma}}}(0) = \mathbf{v}\,. \] By continuity, we can take \(\varepsilon\) small enough so that \[ {\pmb{\gamma}}(-\varepsilon,\varepsilon) \subseteq {\pmb{\sigma}}(U) \,. \] By Lemma 74 there exist smooth functions \(u , v \colon (-\varepsilon,\varepsilon) \to \mathbb{R}\) such that \[ {\pmb{\gamma}}(t) = {\pmb{\sigma}}( u(t), v(t) ) \,, \quad \forall \, t \in (-\varepsilon,\varepsilon) \,, \] and \[ u(0)=u_0 \,, \quad v(0) = v_0 \,. \] Therefore, by chain rule, \[ \dot{{\pmb{\gamma}}}(t) = {\pmb{\sigma}}_u ( u(t),v(t) ) \, \dot{u}(t) + {\pmb{\sigma}}_v ( u(t),v(t) ) \, \dot{v}(t) \,. \] Evaluating the above at \(t=0\) yields \[\begin{align*} \mathbf{v}& = \dot{{\pmb{\gamma}}}(0) \\ & = {\pmb{\sigma}}_u ( u(0),v(0) ) \, \dot{u}(0) + {\pmb{\sigma}}_v ( u(0),v(0) ) \, \dot{v}(0) \\ & = {\pmb{\sigma}}_u ( u_0,v_0 ) \, \dot{u}(0) + {\pmb{\sigma}}_v ( u_0,v_0 ) \, \dot{v}(0) \,, \end{align*}\] which shows \[ \mathbf{v}\in \operatorname{span} \{ {\pmb{\sigma}}_u (u_0,v_0), {\pmb{\sigma}}_v(u_0,v_0) \} \,. \]
Step 2. Suppose that \[ \mathbf{v}\in \operatorname{span} \{ {\pmb{\sigma}}_u (u_0,v_0), {\pmb{\sigma}}_v(u_0,v_0) \} \,. \] Then there exist \(\lambda,\mu \in \mathbb{R}\) such that \[ \mathbf{v}= \lambda {\pmb{\sigma}}_u (u_0,v_0) + \mu {\pmb{\sigma}}_v (u_0,v_0) \,. \] Define the curve \[ {\pmb{\gamma}}(t) := {\pmb{\sigma}}(u_0 + \lambda t, v_0 + \mu t) \,, \quad t \in (-\varepsilon,\varepsilon) \,. \] We have \[ {\pmb{\gamma}}(0) = {\pmb{\sigma}}(u_0,v_0) = \mathbf{p}\,. \] Therefore, for \(\varepsilon\) sufficiently small, we have \[ {\pmb{\gamma}}(-\varepsilon,\varepsilon) \subseteq {\pmb{\sigma}}(U) \,. \] By chain rule \[ \dot{{\pmb{\gamma}}}(t) = {\pmb{\sigma}}_u (u_0+ \lambda t , v_0+ \mu t ) \lambda + {\pmb{\sigma}}_v (u_0+ \lambda t , v_0+ \mu t ) \mu \,, \] and therefore \[ \dot{{\pmb{\gamma}}}(0) = {\pmb{\sigma}}_u (u_0 , v_0 ) \lambda + {\pmb{\sigma}}_v (u_0 ,v_0) \mu = \mathbf{v}\,. \] This proves that \(\mathbf{v}\in T_{\mathbf{p}} \mathcal{S}\), ending the proof.
Therefore \(T_{\mathbf{p}} \mathcal{S}\) is always two-dimensional. This justifies the following definition.
Definition 76: Tangent plane
Remark 77
To see this, take the curve \({\pmb{\gamma}}(t) \equiv \mathbf{p}\). Then \({\pmb{\gamma}}(0) = \mathbf{p}\) and \(\dot{{\pmb{\gamma}}}(0) = {\pmb{0}}\), showing that \({\pmb{0}}\in T_{\mathbf{p}} \mathcal{S}\).
Therefore \(T_{\mathbf{p}} \mathcal{S}\) is a plane through the origin, no matter where the point \(\mathbf{p}\in \mathcal{S}\) is located. When we draw the tangent plane as a plane resting on the surface, see Figure 4.6, we are not drawing \(T_{\mathbf{p}} \mathcal{S}\), but rather the plane \[ \mathbf{p}+ T_{\mathbf{p}} \mathcal{S}\,, \] which is the affine tangent plane through \(\mathbf{p}\in \mathcal{S}\).
It is possible to give a cartesian equation for the tangent plane \[ T_{\mathbf{p}} \mathcal{S} \] and for the affine tangent plane \[ \mathbf{p}+ T_{\mathbf{p}} \mathcal{S}\,. \]
Proposition 78: Equation of tangent plane
Proof
Example 79
First, we need to check that \({\pmb{\sigma}}\) is regular. We have \[\begin{align*} {\pmb{\sigma}}_u & = \left( - \sqrt{1-v} \sin(u) , \sqrt{1-v} \cos(u), 0 \right) \\ {\pmb{\sigma}}_v & = \left( \frac{1}{2} (1-v)^{-1/2} \cos(u) , \frac{1}{2} (1-v)^{-1/2} \sin(u), 1 \right) \end{align*}\] As the last component of \({\pmb{\sigma}}_u\) is \(0\) and the last component of \({\pmb{\sigma}}_v\) is \(1\), we conclude that \({\pmb{\sigma}}_u\) and \({\pmb{\sigma}}_v\) are linearly independent. Thus \({\pmb{\sigma}}\) is regular.
Suppose \(\mathbf{p}\in \mathcal{S}\) is such that \[ {\pmb{\sigma}}(u_0,v_0) = \mathbf{p} \] for some \((u_0,v_0) \in \mathbb{R}^2\). By Theorem 75 we have \[ T_{\mathbf{p}} \mathcal{S}= \operatorname{span} \{ {\pmb{\sigma}}_u (u_0,v_0) , {\pmb{\sigma}}_v (u_0,v_0) \} \,. \] To find the equation of \(T_{\mathbf{p}} \mathcal{S}\) we compute: \[\begin{align*} {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v & = \left| \begin{array}{ccc} \mathbf{i}& \mathbf{j}& \mathbf{k}\\ - \sqrt{1-v} \sin(u) & \sqrt{1-v} \cos(u) & 0 \\ \frac{1}{2} (1-v)^{-1/2} \cos(u) & \frac{1}{2} (1-v)^{-1/2} \sin(u) & 1 \end{array} \right| \\ & = \left( \sqrt{1-v} \cos(u) , \sqrt{1-v} \sin(u), - \frac12 \right) \end{align*}\] For \[ (u_0,v_0) = \left( \frac{\pi}{4}, 0 \right) \] we have \[ \mathbf{p}= {\pmb{\sigma}}(u_0,v_0) = \left( \frac{\sqrt 2}{2}, \frac{\sqrt 2}{2}, 0 \right) \,, \] and therefore \[ \mathbf{n}= ({\pmb{\sigma}}_u \times {\pmb{\sigma}}_v)(u_0,v_0) = \left( \frac{\sqrt 2}{2}, \frac{\sqrt 2}{2} , -\frac{1}{2} \right) \,. \] The equation for \(T_{\mathbf{p}} \mathcal{S}\) is therefore \[ (x,y,z) \cdot \mathbf{n}= 0 \,, \quad \forall \, (x,y,z) \in \mathbb{R}^3 \,. \] The above reads \[ \frac{\sqrt 2}{2} \, x + \frac{\sqrt 2}{2} \, y - \frac{1}{2} \, z = 0 \,. \] The equation for \(\mathbf{p}+ T_{\mathbf{p}} \mathcal{S}\) is instead \[ \frac{\sqrt 2}{2} \, x + \frac{\sqrt 2}{2} \, y - \frac{1}{2} \, z = k \,, \] for some \(k \in \mathbb{R}\). To compute \(k\), note that \(\mathbf{p}\in \mathbf{p}+ T_{\mathbf{p}} \mathcal{S}\), and therefore \[ \frac{\sqrt 2}{2} \, \frac{\sqrt 2}{2} + \frac{\sqrt 2}{2} \, \frac{\sqrt 2}{2} = k \quad \implies \quad k = 1 \,. \] The equation for \(\mathbf{p}+ T_{\mathbf{p}} \mathcal{S}\) is then \[ \frac{\sqrt 2}{2} \, x + \frac{\sqrt 2}{2} \, y - \frac{1}{2} \, z = 1 \,. \]
Remark 80: Tangent space and derivations
The basic idea is as follows: If \(U \subseteq \mathbb{R}^2\) is open and \(\mathbf{p}\in U\), then \(T_{\mathbf{p}} U = \mathbb{R}^2\). We can associate to any point \(\mathbf{v}\in T_{\mathbf{p}} U\) a directional derivative acting on smooth functions \(f \colon U \to \mathbb{R}\): \[ \mathbf{v}= (v_1,v_2) \mapsto \left. \frac{\partial }{\partial v} \right|_p = v_1 \, \left. \frac{\partial }{\partial x_1} \right|_p + v_2 \, \left. \frac{\partial }{\partial x_2} \right|_p \] The above directional derivative is called a derivation.
The point is that derivations do not need to be defined through vectors, but can be defined as follows: \(D\) is a derivation if
- \(D \colon C^{\infty}(U) \to \mathbb{R}\) is a linear operator, where \(C^{\infty}(U)\) is the set of smooth functions \(f \colon U \to \mathbb{R}\),
- \(D\) satisfies the Leibnitz rule \[ D(fg) = f(\mathbf{p}) D(g) + g(\mathbf{p}) D(f) \,, \quad \forall \, f,g \in C^{\infty}(U) \,. \]
The tangent plane at p can then be defined as \[ T_{\mathbf{p}} U = \{ D \, \mbox{ derivation at } \mathbf{p}\} \,. \] Therefore \[ T_{\mathbf{p}} U \subseteq (C^{\infty}(U))^* \,, \] the dual space of smooth functions.
It is possible to do such construction directly on \(\mathcal{S}\), by introducing the concepts of:
- germ of a function
- algebra of derivations, acting on germs
An in depth discussion can be found in Chapter 3.4 of (Abate, Marco and Tovena, Francesca 2011).
4.9 Differential of smooth functions
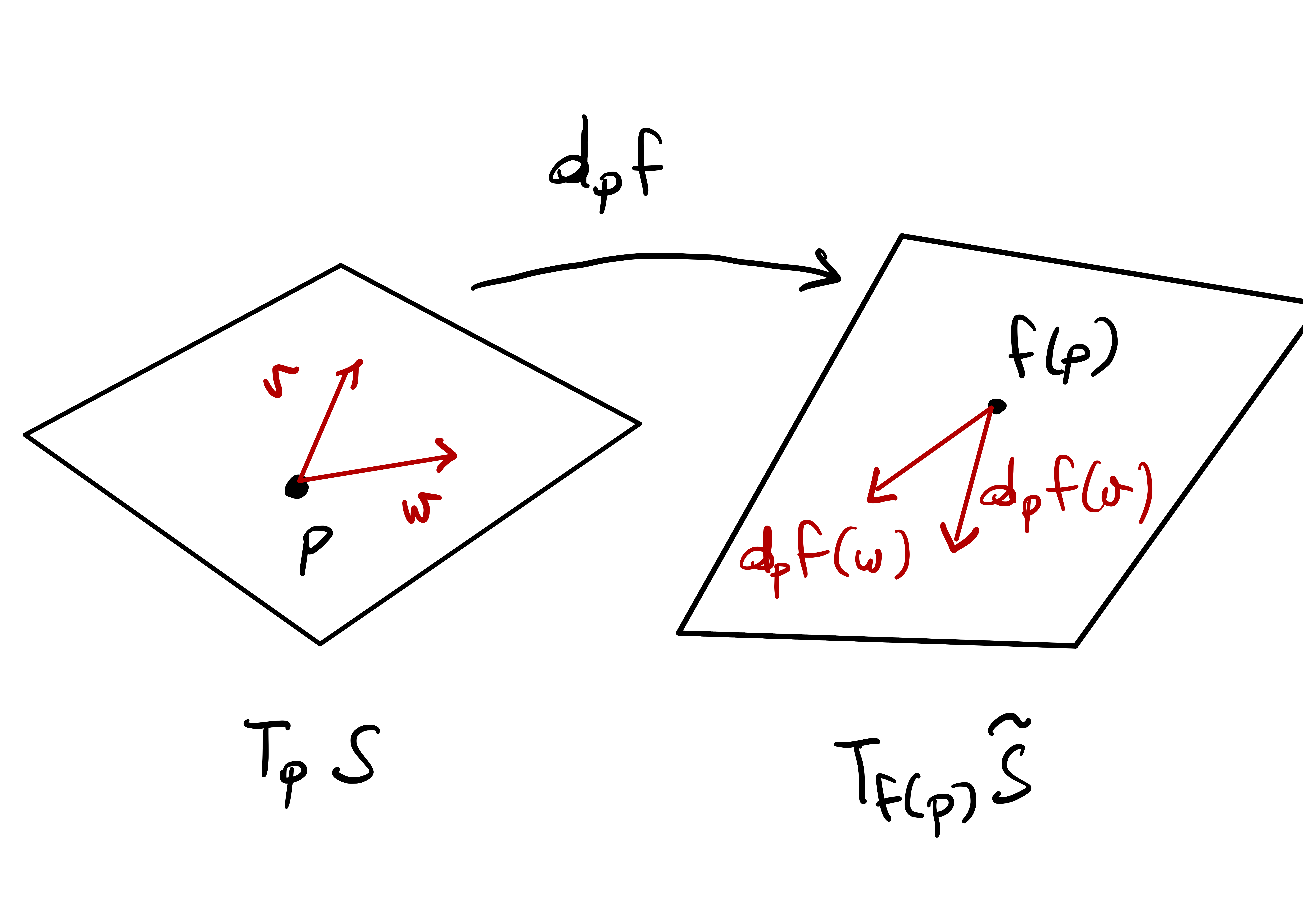
Let \(f \colon U \to V\) with \(U,V \subseteq \mathbb{R}^2\) open. Suppose \(f\) is smooth. The differential of \(f\) at \(\mathbf{p}\in U\) is a linear map \[ df_{\mathbf{p}} \colon \mathbb{R}^2 \to \mathbb{R}^2 \,. \] We have seen that \[ T_{\mathbf{p}} U = \mathbb{R}^2 \] and therefore we can interpret \(df_{\mathbf{p}}\) as a map between tangent planes: \[ df_{\mathbf{p}} \colon \mathbb{R}^2 \to \mathbb{R}^2 \,. \] Similarly, if \(f \colon \mathcal{S}\to \widetilde{\mathcal{S}}\) is a smooth map between surfaces, we can define its differential at \(\mathbf{p}\in \mathcal{S}\) as a linear map \[ df_{\mathbf{p}} \colon T_{\mathbf{p}} \mathcal{S}\to T_{f(\mathbf{p})} \widetilde{\mathcal{S}} \,. \] To define such map, we need the following lemma.
Lemma 81
Proof
Definition 82: Differential of smooth function
We now show that \(df_{\mathbf{p}}\) is well-defined and linear. Moreover we provide a representation of \(df_{\mathbf{p}}\) as a matrix.
Proposition 83
Let \(\mathcal{S}\) and \(\widetilde{\mathcal{S}}\) be regular surfaces and \(f \colon \mathcal{S}\to \widetilde{\mathcal{S}}\) a smooth map. Denote the differential of \(f\) by \[ df_{\mathbf{p}} \colon T_{\mathbf{p}} \mathcal{S}\to T_{f(\mathbf{p})} \widetilde{\mathcal{S}} \,. \] We have:
- \(df_{\mathbf{p}} (\mathbf{v})\) does not depend on the choice of \({\pmb{\gamma}}\).
- \(df_{\mathbf{p}}\) is linear, that is, \[ df_{\mathbf{p}} (\lambda \mathbf{v}+ \mu \mathbf{w}) = \lambda df_{\mathbf{p}} (\mathbf{v}) + \mu df_{\mathbf{p}} (\mathbf{w}) \,, \] for all \(\mathbf{v},\mathbf{w}\in T_{\mathbf{p}} \mathcal{S}\) and \(\lambda,\mu \in \mathbb{R}\).
- Let \[ {\pmb{\sigma}}\colon U \to \mathcal{S}\,, \quad \widetilde{{\pmb{\sigma}}} \colon \widetilde{U} \to \widetilde{\mathcal{S}} \,, \] be regular charts at \(\mathbf{p}\) and \(f(\mathbf{p})\), respectively. Denote by \[ (u,v) \mapsto ( \alpha(u,v), \beta(u,v) ) \] the components of the smooth map \[ \Psi := \widetilde{{\pmb{\sigma}}}^{-1} \circ f \circ {\pmb{\sigma}}\colon U \to \widetilde{U} \,. \] In particular \[ \widetilde{{\pmb{\sigma}}} ( \alpha(u,v) , \beta(u,v) ) = f({\pmb{\sigma}}(u,v)) \,, \quad \forall \, (u,v) \in U \,. \] The matrix of the linear map \(df_{\mathbf{p}}\) with respect to the basis \[ \{ {\pmb{\sigma}}_u , {\pmb{\sigma}}_v \} \,\, \mbox{ on } \,\, T_{\mathbf{p}} \mathcal{S}\,, \quad \{ \widetilde{{\pmb{\sigma}}}_{\tilde{u}} , \widetilde{{\pmb{\sigma}}}_{\tilde{v}} \} \,\, \mbox{ on } \,\, T_{f(\mathbf{p})} \widetilde{\mathcal{S}} \,, \] is given by the Jacobian of the map \(\Psi\), that is, \[ d_{\mathbf{p}} f = J\Psi = \left( \begin{array}{cc} \alpha_u & \alpha_v \\ \beta_u & \beta_v \\ \end{array} \right) \,. \]
For a proof, see the discussion at page \(87\) of (Pressley 2010).
Proposition 84
The following hold:
If \(\mathcal{S}\) is a regular surface and \(\mathbf{p}\in \mathcal{S}\), the differential at \(\mathbf{p}\) of the identity map \[ I \colon \mathcal{S}\to \mathcal{S}\,, \quad I(x):=x \,, \] is the identity map \[ I \colon T_{\mathbf{p}} (\mathcal{S}) \to T_{\mathbf{p}} (\mathcal{S}) \,, \quad I(v):=v \,. \]
If \(\mathcal{S}_1\), \(\mathcal{S}_2\) and \(\mathcal{S}_3\) are regular surfaces and \[ f \colon \mathcal{S}_1 \to \mathcal{S}_2 \,, \quad g \colon \mathcal{S}_2 \to \mathcal{S}_3 \,, \] are smooth maps, then \[ d_{\mathbf{p}} ( g \circ f ) = d_{f(\mathbf{p})} g \circ d_{\mathbf{p}} f \,, \] for all \(\mathbf{p}\in T_{\mathbf{p}} \mathcal{S}_1\).
If \(\mathcal{S}_1\), \(\mathcal{S}_2\) are regular surfaces and \[ f \colon \mathcal{S}_1 \to \mathcal{S}_2 \,, \] is a diffeomorphism, then the differential \[ d_{\mathbf{p}} \colon T_{\mathbf{p}} \mathcal{S}_1 \to T_{f(\mathbf{p})} \mathcal{S}_2 \] is invertible for all \(\mathbf{p}\in \mathcal{S}_1\).
For a proof see Proposition 4.4.5 in (Pressley 2010). The above proposition says that the differential of diffeomorphism is invertible. The converse statement is true locally.
Theorem 85
Let \(\mathcal{S}_1\) and \(\mathcal{S}_2\) be regular surfaces. Suppose that \[ f \colon \mathcal{S}_1 \to \mathcal{S}_2 \] is smooth. They are equivalent:
- \(f\) is a local diffeomorphism.
- The differential \(d_{\mathbf{p}} f \colon T_{\mathbf{p}} \mathcal{S}_1 \to T_{f(\mathbf{p})} \mathcal{S}_2\) is invertible for all \(\mathbf{p}\in \mathcal{S}_1\).
The proof is based on the Inverse Function Theorem, see Proposition 4.4.6 in (Pressley 2010).
4.10 Examples of Surfaces
4.10.1 Level surfaces
We have already seen level surfaces. Let us recall the defintion.
Definition 86: Level surface
The following Theorem gives a sufficient condition for \(\mathcal{S}_f\) to be a regular surface.
Theorem 87
Let us give a characterization of the tangent plane to \(\mathcal{S}_f\).
Proposition 88
Proof
4.10.2 Quadrics
Quadrics are level surfaces \[ S_f = \left\{ (x,y,z) \in \mathbb{R}^3 \, \colon \,f(x,y,z) = 0 \right\} \,, \] where \[\begin{align*} f(x,y,z) = & a_1 x^2 + a_2 y^2 + a_3 z^2 + 2a_4 xy + 2a_5 xz + 2a_6 yz + \\ & + b_1 x + b_2 y + b_3 z + c \,, \end{align*}\] for some coefficients \(a_i,b_i,c \in \mathbb{R}\). Let \[ A = \left( \begin{array}{ccc} a_1 & a_4 & a_6 \\ a_4 & a_2 & a_5 \\ a_6 & a_5 & a_3 \end{array} \right) \in \mathbb{R}^{3 \times 3} \,, \] and \[ \mathbf{x}= (x,y,z)^T \,, \quad \mathbf{b} = (b_1,b_2,b_3)^T \,. \] Then \(f\) can be represented by the quadratic form \[ f(\mathbf{x}) = \mathbf{x}^T A \mathbf{x}+ \mathbf{b} \cdot \mathbf{x}+ c \,. \] The expression \(f=0\) is called a quadric equation.
As stated in the following theorem, there are \(14\) quadrics in total. Out of these:
- 9 are interesting surfaces,
- 3 are planes,
- 1 is a line,
- 1 is a point.
Theorem 89
Suppose \(\mathcal{S}\) is a level surface defined by a quadric equation. Then, up to rigid motions, \(\mathcal{S}\) can be described by one of the following equations:
Ellipsoid: \(\dfrac{x^2}{p^2} + \dfrac{y^2}{q^2} + \dfrac{z^2}{r^2} = 1\).
Hyperboloid of one sheet: \(\dfrac{x^2}{p^2} + \dfrac{y^2}{q^2} - \dfrac{z^2}{r^2} = 1\)
Hyperboloid of two sheets: \(\dfrac{x^2}{p^2} - \dfrac{y^2}{q^2} - \dfrac{z^2}{r^2} = 1\)
Elliptic Paraboloid: \(\dfrac{x^2}{p^2} + \dfrac{y^2}{q^2} = z\)
Hyperbolic Paraboloid: \(\dfrac{x^2}{p^2} - \dfrac{y^2}{q^2} = z\)
Quadric Cone: \(\dfrac{x^2}{p^2} + \dfrac{y^2}{q^2} - \dfrac{z^2}{r^2} = 0\)
Elliptic Cylinder: \(\dfrac{x^2}{p^2} + \dfrac{y^2}{q^2} = 1\)
Hyperbolic Cylinder: \(\dfrac{x^2}{p^2} - \dfrac{y^2}{q^2} = 1\)
Parabolic Cylinder: \(\dfrac{x^2}{p^2} = y\)
Plane: \(x = 0\)
Two parallel planes: \(x^2 = p^2\)
Two intersecting planes: \(\dfrac{x^2}{p^2} - \dfrac{y^2}{q^2} = 0\)
Straight line: \(\dfrac{x^2}{p^2} + \dfrac{y^2}{q^2} = 0\)
Single point: \(\dfrac{x^2}{p^2} + \dfrac{y^2}{q^2} + \dfrac{z^2}{r^2} = 0\)
The proof of Theorem 89 follows by diagonalizing the symmetric matrix \(A\), and by studying the eigenvalues, see Theorem 5.5.2 in (Pressley 2010).
Example 90
Example 91
4.10.3 Ruled surfaces
A ruled surface is a surface obtained as union of straight lines, called the rulings of the surface. By using curves, ruled surfaces can be defined in the following way.
Definition 92: Ruled surface
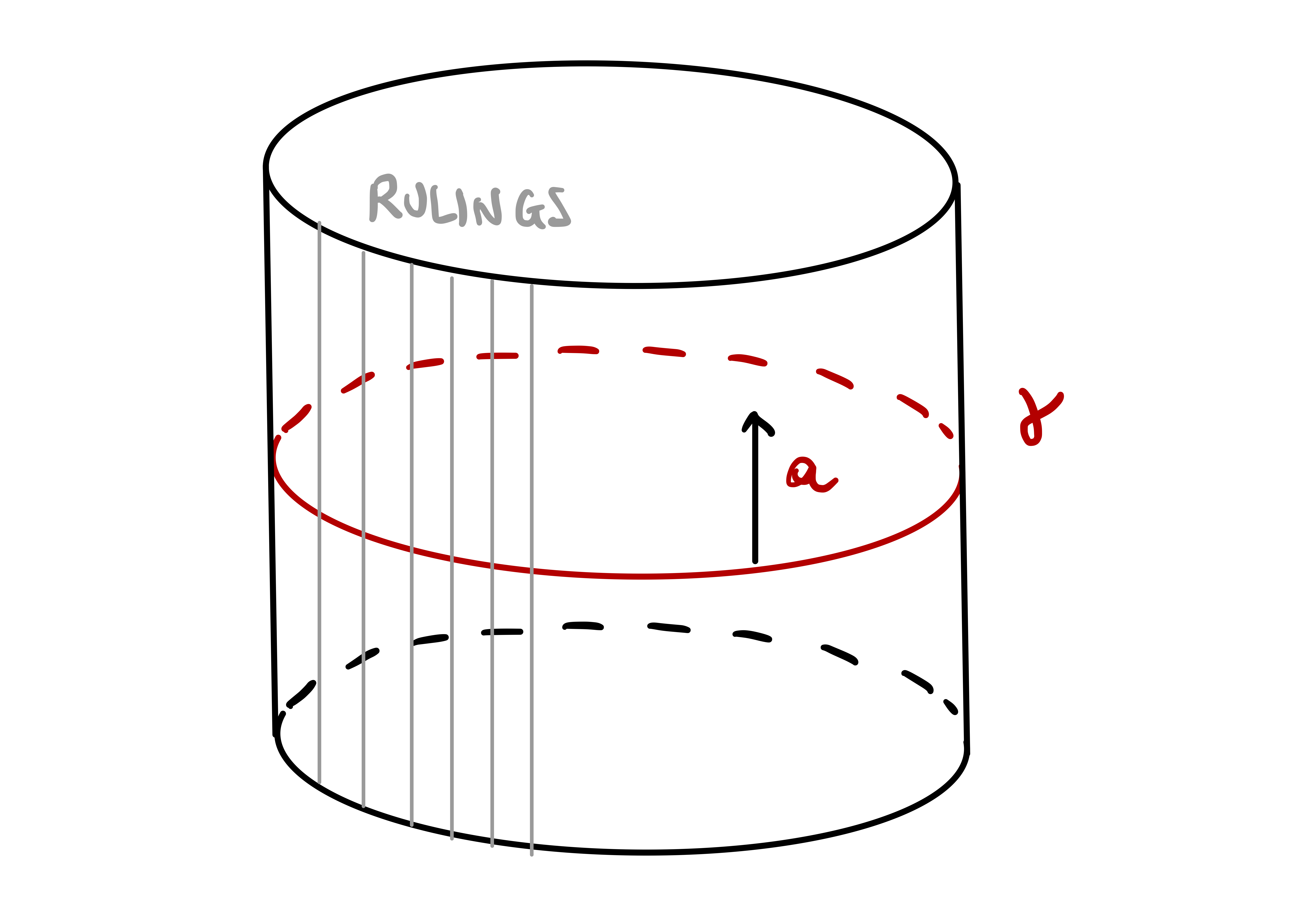
Let \({\pmb{\gamma}}\colon (a,b) \to \mathbb{R}^3\) be a smooth curve and \(\mathbf{a} \colon (a,b) \to \mathbb{R}^3\) a vector, such that \(\dot{{\pmb{\gamma}}}(t)\) and \(\mathbf{a}(t)\) are linearly independent for all \(t \in (a,b)\). A ruled surface is a surface with chart \[ {\pmb{\sigma}}(u,v) = {\pmb{\gamma}}(u) + v \mathbf{a}(u) \,. \] We say that:
- \({\pmb{\gamma}}\) is the base curve
- The lines \(v \mapsto v \mathbf{a}(u)\) are the rulings
Proposition 93
Proof
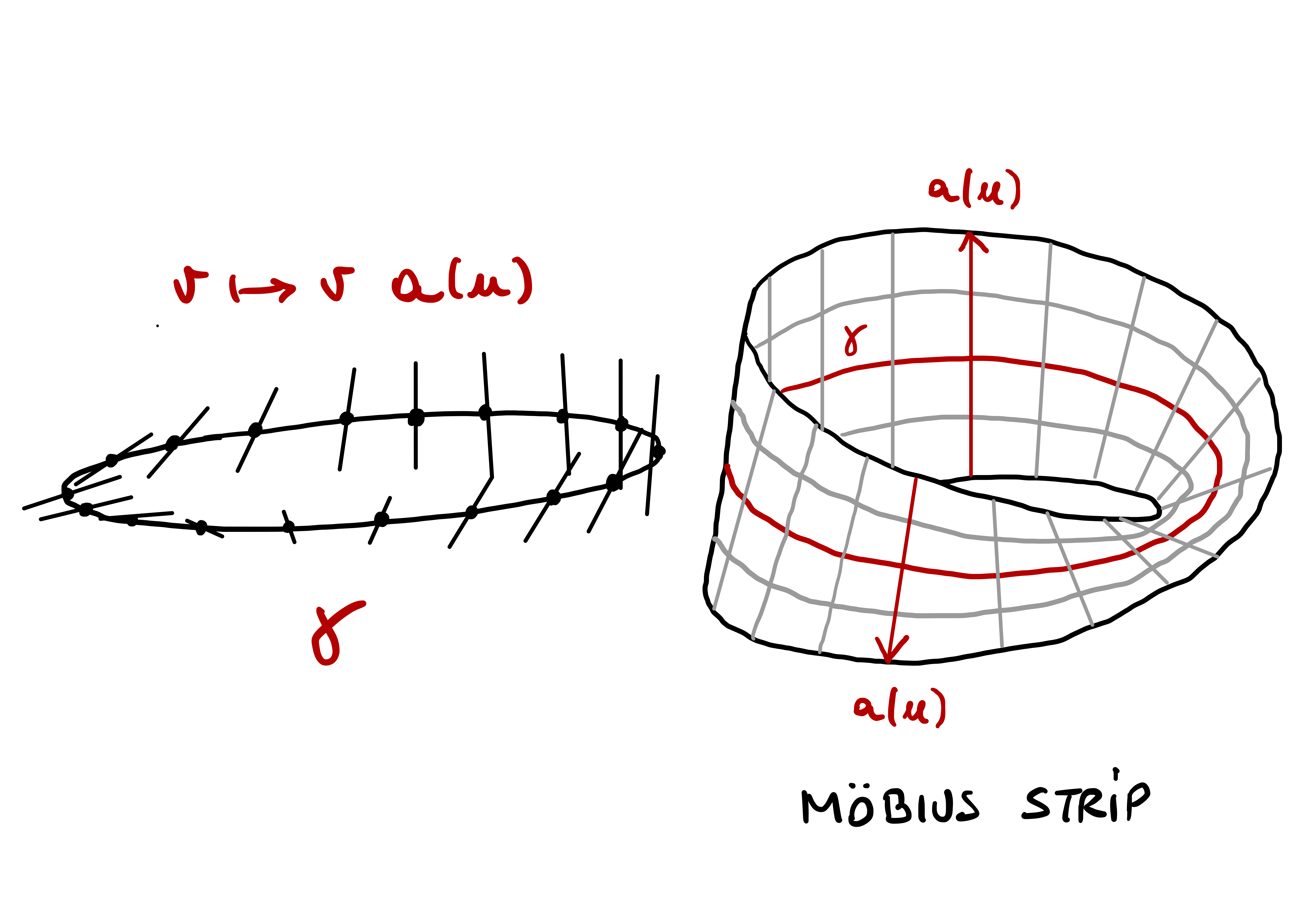
The same base curve can yield multiple ruled surfaces. For example, if \({\pmb{\gamma}}\) is a circle, we can obtain both the unit cylinder and the Möbius band.
Example 94: Unit Cylinder
Example 95: Möbius band
4.10.4 Surfaces of Revolution
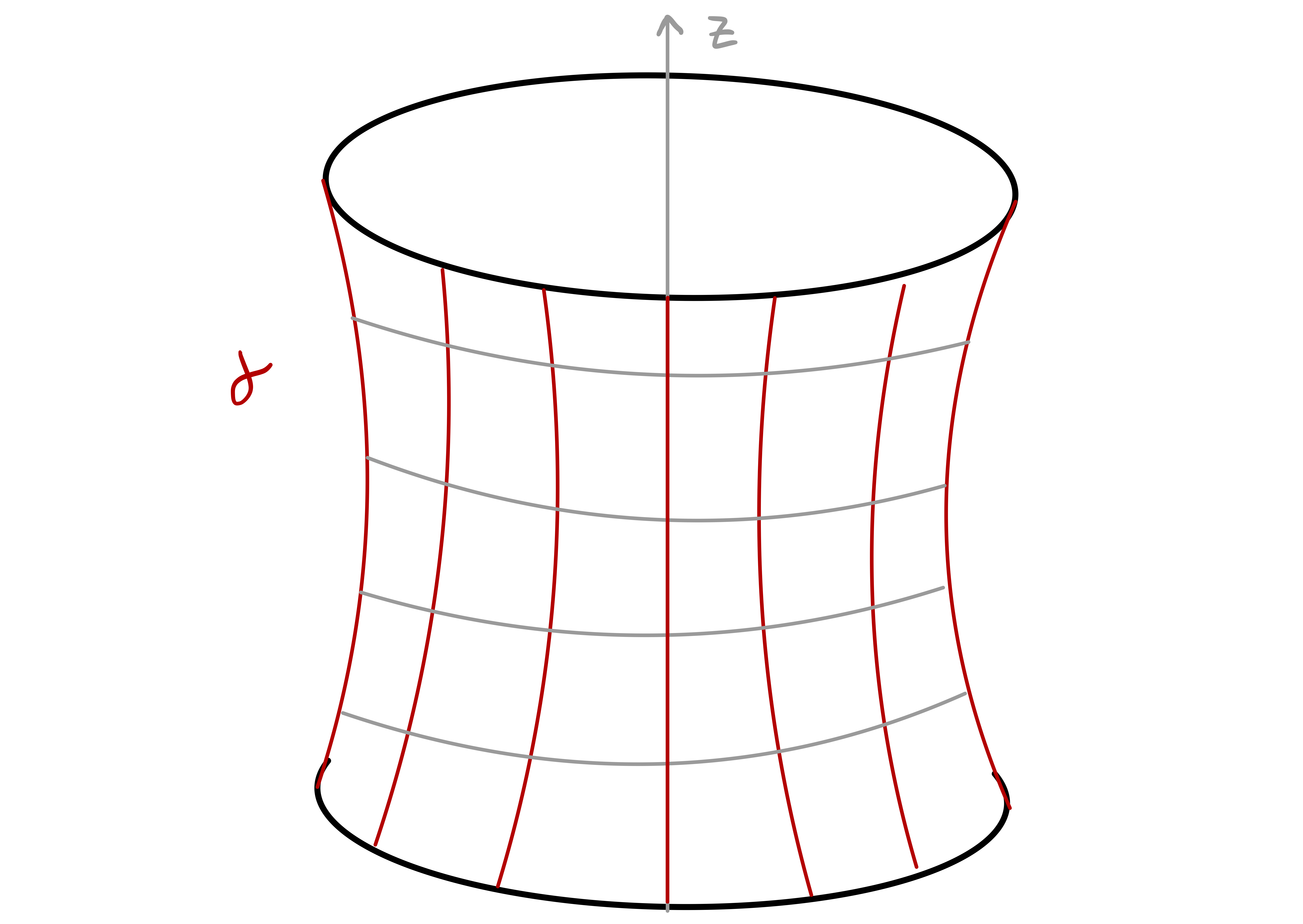
Surfaces of revolution are obtained by rotating a curve about the \(z\)-axis.
Definition 96: Surface of revolution
Proposition 97
Proof
Example 98: Catenoid
4.11 First fundamental form
In this section we introduce the first fundamental form of a surface. This will allow us to compute:
- Inner product between tangent vectors
- Angle between tangent vectors
- Area of surface regions
Moreover we can compute
- Length of curves on a surface
- Angle between curves on a surface
4.11.1 Length on surfaces
Let \(\mathcal{S}\) be a surface and consider two points \(\mathbf{p}, \mathbf{q} \in \mathcal{S}\). The euclidean distance between \(\mathbf{p}\) and \(\mathbf{q}\) is \[ \left\| \mathbf{p}- \mathbf{q} \right\| \,. \] However this measures the length of the straight segment which connects \(\mathbf{p}\) to \(\mathbf{q}\). We are interested in measuring the distance on \(\mathcal{S}\). A way to measure such distance is the following: Suppose \[ {\pmb{\gamma}}\colon (t_0,t_1) \to \mathcal{S} \] is a smooth curve such that \[ {\pmb{\gamma}}(t_0) = \mathbf{p}\,, \quad {\pmb{\gamma}}(t_1) = \mathbf{q} \,. \] The distance between \(\mathbf{p}\) and \(\mathbf{q}\) on \(\mathcal{S}\) is the length of \({\pmb{\gamma}}\), i.e., \[ \int_{t_0}^{t_1} \left\| \dot{{\pmb{\gamma}}}(t) \right\| \, dt \,. \]
Question 99
Since \({\pmb{\gamma}}(t) \in \mathcal{S}\), by definition we have \[ \dot{{\pmb{\gamma}}}(t) \in T_{\mathbf{x}} S \,, \quad \mathbf{x}:= {\pmb{\gamma}}(t) \,. \] Therefore, computing \(\left\| \dot{{\pmb{\gamma}}}(t) \right\|\) is equivalent to computing the length of tangent vectors. This motivates the definition of first fundamental form.
Definition 100: First fundamental form
Three observations:
The first fundamental form of \(\mathcal{S}\) at \(\mathbf{p}\) is the map obtained by restricting the scalar product of \(\mathbb{R}^3\) to \(T_{\mathbf{p}} \mathcal{S}\).
Note that \[ I_{\mathbf{p}} (\mathbf{v},\mathbf{v}) = \| \mathbf{v}\|^2 \,, \] so that \(I_{\mathbf{p}}\) can be used to compute the length of tangent vectors.
The definition of \(I_{\mathbf{p}}\) does not depend on a chosen chart.
To use the first fundamental form in practice, we need to express \(I_{\mathbf{p}}\) in terms of local charts. To this end, we first define the coordinates functions \(du\) and \(dv\) on \(T_{\mathbf{p}} S\).
Definition 101: Coordinate functions on tangent plane
Definition 102: First fundamental form of a chart
We usually omit the dependence on \(\mathbf{v}\) in (4.3), and write \[ \mathscr{F}_1 = E \, du^2 + 2F \, du \, dv + G \, dv^2 \,. \] The quadratic form \(\mathscr{F}_1\) is related to \(I_{\mathbf{p}}\) in the following way.
Proposition 103
Proof
Remark 104: Linear algebra interpretation
Notation
Remark 105: First fundamental form and reparametrizations
The first fundamental form \(I_{\mathbf{p}}\) depends only on the surface \(\mathcal{S}\) and the point \(\mathbf{p}\). Instead the representation of \(I_{\mathbf{p}}\) \[ \mathscr{F}_1 = E \, du^2 + 2F \, du dv + G \, dv^2 \] depends on the choice of chart \({\pmb{\sigma}}\colon U \to \mathbb{R}^3\). Indeed suppose that \(\widetilde{{\pmb{\sigma}}} \colon \widetilde{U} \to \mathbb{R}^3\) is a reparametrization of \({\pmb{\sigma}}\), that is, \[ \widetilde{{\pmb{\sigma}}} = {\pmb{\sigma}}\circ \Phi \,, \] where \(\Phi \colon \widetilde{U} \to U\) is a diffeomorphism. Recall that we denote the components \(\Phi^1\) and \(\Phi^2\) of \(\Phi\) by \[ (\tilde{u}, \tilde{v}) \mapsto u (\tilde{u}, \tilde{v}) \,, \quad (\tilde{u}, \tilde{v}) \mapsto v (\tilde{u}, \tilde{v}) \,, \] respectively. The Jacobian of \(\Phi\) is then \[ J\Phi = \left( \begin{array}{cc} \dfrac{\partial u}{\partial \tilde u} & \dfrac{\partial u}{\partial \tilde v} \\ \dfrac{\partial v}{\partial \tilde u} & \dfrac{\partial v}{\partial \tilde v} \end{array} \right) \,. \] Denote the first fundamental form of \(\widetilde{{\pmb{\sigma}}}\) by \[ \widetilde{\mathscr{F}}_1 = \widetilde{E} \, d\tilde{u}^2 + 2 \widetilde{F} \, d\tilde{u} d\tilde{v} + \widetilde{G} \, d\tilde{v}^2 \,. \] The linear maps \(du, dv\) and \(d\tilde{u}, d\tilde{v}\) are related by \[ du = \frac{\partial u}{\partial \tilde{u}} \, d\tilde{u} + \frac{\partial u}{\partial \tilde{v}} \, d\tilde{v} \,, \quad dv = \frac{\partial v}{\partial \tilde{u}} \, d\tilde{u} + \frac{\partial v}{\partial \tilde{v}} \, d\tilde{v} \tag{4.4}\] Moreover the matrices of \(\mathscr{F}_1\) and \(\widetilde{\mathscr{F}}_1\) are related by \[ \left( \begin{array}{cc} \widetilde{E} & \widetilde{F} \\ \widetilde{F} & \widetilde{G} \end{array} \right) = (J \Phi)^T \, \left( \begin{array}{cc} E & F \\ F & G \end{array} \right) \, J \Phi \,. \tag{4.5}\]
The proof of the above statements follows by basic linear algebra: The pairs \(\{{\pmb{\sigma}}_u,{\pmb{\sigma}}_u\}\) and \(\{\widetilde{{\pmb{\sigma}}}_{\tilde{u}} , \widetilde{{\pmb{\sigma}}}_{\tilde{v}} \}\) are bases for the vector space \(T_{\mathbf{p}} \mathcal{S}\). The change of basis matrix is given exactly by \(J\Phi\). Therefore formulas (4.4) and (4.5) are consequence of change of basis results for linear maps and bilinear forms, respectively.
Let us compute the first fundamental form of a plane and of a cylinder.
Example 106: Plane
Let \(\mathbf{a}, \mathbf{p}, \mathbf{q} \in \mathbb{R}^3\). Suppose that \(\mathbf{p}\) and \(\mathbf{q}\) are orthonormal vectors, that is, \[ \left\| \mathbf{p} \right\| = \left\| \mathbf{q} \right\| = 1 \,, \quad \mathbf{p}\cdot \mathbf{q} = 0 \,. \] Consider the plane with chart \[ {\pmb{\sigma}}(u,v) = \mathbf{a} + u \mathbf{p}+ v \mathbf{q} \,, \quad (u,v) \in \mathbb{R}^2 \,. \] Prove that the first fundamental form of \({\pmb{\sigma}}\) is \[ \mathscr{F}_1 = du^2 + dv^2 \,. \]
We have \[ {\pmb{\sigma}}_u = \mathbf{p}\,, \quad {\pmb{\sigma}}_v = \mathbf{q} \] and therefore \[\begin{align*} E & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_u = \left\| \mathbf{p} \right\|^2 = 1 \\ F & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v = \mathbf{p}\cdot \mathbf{q} = 0 \\ G & = {\pmb{\sigma}}_v \cdot {\pmb{\sigma}}_v = \left\| \mathbf{q} \right\|^2 = 1 \\ \end{align*}\] Then the first fundamental form is \[ \mathscr{F}_1 = E \, du^2 + 2 F\, du \, dv + G \, dv^2 = du^2 + dv^2 \,. \]
Two remarks concerning Example 106 :
- The above example should not be surprising, since distances on a plane are the same as Euclidean distances, given that straight segments are contained in the plane.
- If we drop the assumption of \(\mathbf{p}\) and \(\mathbf{q}\) being orthonormal, then \[ \mathscr{F}_1 = \left\| \mathbf{p} \right\|^2 \, du^2 + \mathbf{p}\cdot \mathbf{q} \, du \, dv + \left\| \mathbf{q} \right\|^2 \, dv^2 \,. \] Again, this is not surprising, due to Remark 105.
Example 107: Unit cylinder
Consider the unit cylinder with chart \[ {\pmb{\sigma}}(u,v) = (\cos(u), \sin(u), v) \,, \quad (u,v) \in (0,2\pi) \times \mathbb{R}\,. \] Prove that the first fundamental form of \({\pmb{\sigma}}\) is \[ \mathscr{F}_1 = du^2 + dv^2 \,. \]
We have \[ {\pmb{\sigma}}_u = (-\sin(u),\cos(u), 0 ) \,, \quad {\pmb{\sigma}}_v = (0,0,1) \,, \] and therefore \[\begin{align*} E & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_u = 1 \\ F & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v = 0 \\ G & = {\pmb{\sigma}}_v \cdot {\pmb{\sigma}}_v = 1 \\ \end{align*}\] Then the first fundamental form is \[ \mathscr{F}_1 = E \, du^2 + 2 F\, du \, dv + G \, dv^2 = du^2 + dv^2 \,. \]
Remark 108
4.11.2 Length of curves
Let us show how the first fundamental form allows to compute the length of curves with values on surfaces.
Proposition 109
Proof
Example 110: Cone
Consider the cone with chart \[ {\pmb{\sigma}}(u,v)=(u \cos(v), u \sin (v), u) \,, \] where \(u > 0\) and \(v \in [0,2\pi]\).
Prove that the first fundamental form of \({\pmb{\sigma}}\) is \[ \mathscr{F}_1 = 2 \, du^2 + u^2 \, dv^2 \,. \]
Let \({\pmb{\gamma}}(t):= {\pmb{\sigma}}(t,t)\). Show that \[ \int_{\pi/2}^{\pi} \left\| \dot{{\pmb{\gamma}}}(t) \right\| \, dt = \int_{\pi/2}^{\pi} \sqrt{ 2 + t^2 } \, dt \,. \]
We have \[ {\pmb{\sigma}}_u = (\cos(v), \sin (v), 1) \,, \quad {\pmb{\sigma}}_v = (- u \sin(v), u \cos (v), 0) \,. \] Therefore \[\begin{align*} E & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_u = \cos^2(v) + \sin^2 (v) + 1 = 2 \\ F & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v = - u \cos(v) \sin(v) + u \cos(v) \sin(v) = 0 \\ G & = {\pmb{\sigma}}_v \cdot {\pmb{\sigma}}_v = u^2 \sin^2(v) + u^2 \cos^2(v) = u^2 \end{align*}\] The first fundamental form of \({\pmb{\sigma}}\) is \[ \mathscr{F}_1 = 2 \, du^2 + u^2 \, dv^2 \,. \] Concering the curve \({\pmb{\gamma}}\), we have \[ {\pmb{\gamma}}(t) := {\pmb{\sigma}}(t,t) \,, \] so that \[ u(t) = t \,, \quad v(t) = t \,. \] In particular \[ \dot u = 1\,, \quad \dot v = 1 \] and \[\begin{align*} E(u(t),v(t)) & = E(t,t) = 2 \\ F(u(t),v(t)) & = F(t,t) = 0 \\ G(u(t),v(t)) & = G(t,t) = t^2 \,. \end{align*}\] By Proposition 109 we have \[\begin{align*} \int_{\pi/2}^{\pi} \left\| \dot{{\pmb{\gamma}}}(t) \right\| \, dt & = \int_{\pi/2}^{\pi} \sqrt{ E \dot{u}^2 + 2F \dot u \dot v + G \dot{v}^2 } \, dt \\ & = \int_{\pi/2}^{\pi} \sqrt{ 2 + t^2 } \, dt \,. \end{align*}\]
4.11.3 Local isometries
We have seen that a plane \(\pmb{\pi}\) and a cylinder \(\mathcal{C}\) have the same first fundamental form. This means that scalar product on the two surfaces is the same, as is the length of curves. In this case we say that \(\pmb{\pi}\) and \(\mathcal{C}\) are locally isometric. Let us give a general definition of such concept.
Definition 111: Local isometry
Notation
Remark 112
A local diffeomorphism \(f \colon \mathcal{S}\to \widetilde{\mathcal{S}}\) is a local isometry if and only if \[ \left\langle \mathbf{v},\mathbf{v} \right\rangle = \left\langle \mathbf{v},\mathbf{v} \right\rangle_f \,, \quad \forall \, \mathbf{v}\in T_{\mathbf{p}} \mathcal{S}\,. \]
The proof follows from the elementary identity \[ \mathbf{v}\cdot \mathbf{w}= \frac12 \left( (\mathbf{v}+ \mathbf{w}) \cdot (\mathbf{v}+ \mathbf{w}) - \mathbf{v}\cdot \mathbf{v}- \mathbf{w}\cdot \mathbf{w}\right) \,, \] which holds for all \(\mathbf{v}, \mathbf{w}\in T_{\mathbf{p}} \mathcal{S}\) (and more in general in arbitrary vector spaces with inner product).
Local isometries preserve the length of curves, as shown in the following proposition.
Proposition 113
Let \(\mathcal{S}\) and \(\widetilde{\mathcal{S}}\) be regular surfaces and \(f \colon \mathcal{S}\to \widetilde{\mathcal{S}}\) be a local diffeomorphism. They are equivalent:
- \(f\) is a local isometry
- Let \({\pmb{\gamma}}\) be a curve in \(\mathcal{S}\) and consider the curve \(\widetilde{{\pmb{\gamma}}}= f \circ {\pmb{\gamma}}\) on \(\widetilde{\mathcal{S}}\). Then \({\pmb{\gamma}}\) and \(\widetilde{{\pmb{\gamma}}}\) have the same length.
Proof
Part 2. Let \(\mathbf{v}\in T_{\mathbf{p}} \mathcal{S}\). Then there exists a curve \({\pmb{\gamma}}\colon (-\varepsilon,\varepsilon) \to \mathcal{S}\) such that \[ {\pmb{\gamma}}(0) = \mathbf{p}\,, \quad \dot{{\pmb{\gamma}}}(0) = \mathbf{v}\,. \] Define the curve \(\widetilde{{\pmb{\gamma}}}:= f \circ {\pmb{\gamma}}\colon (-\varepsilon,\varepsilon) \to \widetilde{\mathcal{S}}\). By assumption \({\pmb{\gamma}}\) and \(\widetilde{{\pmb{\gamma}}}\) have the same length, that is, \[ \int_{-\varepsilon}^{\varepsilon} \sqrt{ \dot{\widetilde{{\pmb{\gamma}}}}(t) \cdot \dot{\widetilde{{\pmb{\gamma}}}}(t) }\, dt = \int_{-\varepsilon}^{\varepsilon} \sqrt{ \dot{{\pmb{\gamma}}}(t) \cdot \dot{{\pmb{\gamma}}}(t) }\, dt \,. \] Since the above is true for each \(\varepsilon>0\), we infer \[ \dot{\widetilde{{\pmb{\gamma}}}}(0) \cdot \dot{\widetilde{{\pmb{\gamma}}}}(0) = \dot{{\pmb{\gamma}}}(0) \cdot \dot{{\pmb{\gamma}}}(0) \,. \] Recall that by definition of differential we have \[ df_{\mathbf{p}} (\mathbf{v}) = \dot{\widetilde{{\pmb{\gamma}}}}(0) \,. \] Therefore \[\begin{align*} df_{\mathbf{p}} (\mathbf{v}) \cdot df_{\mathbf{p}} (\mathbf{v}) & = \dot{\widetilde{{\pmb{\gamma}}}}(0) \cdot \dot{\widetilde{{\pmb{\gamma}}}}(0) \\ & = \dot{{\pmb{\gamma}}}(0) \cdot \dot{{\pmb{\gamma}}}(0) \\ & = \mathbf{v}\cdot \mathbf{v}\,. \end{align*}\] As \(\mathbf{v}\) was arbitrary, we showed that \[ df_{\mathbf{p}} (\mathbf{v}) \cdot df_{\mathbf{p}} (\mathbf{v}) = \mathbf{v}\cdot \mathbf{v}\,, \quad \forall \, \mathbf{v}\in T_{\mathbf{p}}(\mathcal{S}) \,. \] Thanks to Remark 112 we conclude that \(f\) is a local isometry.
We have seen that local isometries preserve the length of curves. It also happen that they preserve the first fundamental form.
Theorem 114
Let \(\mathcal{S}\) and \(\widetilde{\mathcal{S}}\) be regular surfaces and \(f \colon \mathcal{S}\to \widetilde{\mathcal{S}}\) be a local diffeomorphism. They are equivalent:
- \(f\) is a local isometry.
- Let \({\pmb{\sigma}}\colon U \to \mathcal{S}\) be a regular chart of \(\mathcal{S}\) and consider the chart of \(\widetilde{\mathcal{S}}\) given by
\[ \widetilde{{\pmb{\sigma}}} = f \circ {\pmb{\sigma}}\colon U \to \widetilde{\mathcal{S}} \,. \] Then \({\pmb{\sigma}}\) and \(\widetilde{{\pmb{\sigma}}}\) have the same first fundamental form, that is, \[ E = \widetilde{E} \,, \quad F = \widetilde{F} \,, \quad G = \widetilde{G} \,, \] where \[\begin{align*} E & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_u \,, \quad F = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v \,, \quad G = {\pmb{\sigma}}_v \cdot {\pmb{\sigma}}_v \,, \\ \widetilde{E} & = \widetilde{{\pmb{\sigma}}}_u \cdot \widetilde{{\pmb{\sigma}}}_u \,, \quad \widetilde{F} = \widetilde{{\pmb{\sigma}}}_u \cdot \widetilde{{\pmb{\sigma}}}_v \,, \quad \widetilde{G} = \widetilde{{\pmb{\sigma}}}_v \cdot \widetilde{{\pmb{\sigma}}}_v \,. \end{align*}\]
Proof
Part 2. Define \(\widetilde{{\pmb{\sigma}}} = f \circ {\pmb{\sigma}}\) and suppose that \({\pmb{\sigma}}\) and \(\widetilde{{\pmb{\sigma}}}\) have the same first fundamental form. In particular they hold \[\begin{align*} {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_u & = \widetilde{{\pmb{\sigma}}}_u \cdot \widetilde{{\pmb{\sigma}}}_u \\ {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v & = \widetilde{{\pmb{\sigma}}}_u \cdot \widetilde{{\pmb{\sigma}}}_v \\ {\pmb{\sigma}}_v \cdot {\pmb{\sigma}}_v & = \widetilde{{\pmb{\sigma}}}_v \cdot \widetilde{{\pmb{\sigma}}}_v \end{align*}\] As discussed above, since \(\widetilde{{\pmb{\sigma}}} = f \circ {\pmb{\sigma}}\), by Proposition 83 we get \[ d_{\mathbf{p}} f({\pmb{\sigma}}_u) = \widetilde{{\pmb{\sigma}}}_u \,, \quad d_{\mathbf{p}} f({\pmb{\sigma}}_v) = \widetilde{{\pmb{\sigma}}}_v \,. \] Let \(\mathbf{v}\in T_{\mathbf{p}} \mathcal{S}\). Since \(\{{\pmb{\sigma}}_u,{\pmb{\sigma}}_v\}\) is a basis for \(T_{\mathbf{p}} \mathcal{S}\) we get \[ \mathbf{v}= \lambda {\pmb{\sigma}}_u + \mu {\pmb{\sigma}}_v \] for some \(\lambda,\mu \in \mathbb{R}\). Therefore \[\begin{align*} d_{\mathbf{p}} f (\mathbf{v}) & = d_{\mathbf{p}} f(\lambda {\pmb{\sigma}}_u + \mu {\pmb{\sigma}}_v ) \\ & = \lambda \, d_{\mathbf{p}} f ({\pmb{\sigma}}_u) + \mu \, d_{\mathbf{p}} f ({\pmb{\sigma}}_v)\\ & = \lambda \widetilde{{\pmb{\sigma}}}_u + \mu \widetilde{{\pmb{\sigma}}}_v \,. \end{align*}\] Hence \[\begin{align*} \mathbf{v}\cdot \mathbf{v}& = ( \lambda {\pmb{\sigma}}_u + \mu {\pmb{\sigma}}_v ) \cdot (\lambda {\pmb{\sigma}}_u + \mu {\pmb{\sigma}}_v) \\ & = \lambda^2 ({\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v) + 2 \lambda\mu ({\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v) + \mu^2 ({\pmb{\sigma}}_v \cdot {\pmb{\sigma}}_v) \\ & = \lambda^2 ( \widetilde{{\pmb{\sigma}}}_u \cdot \widetilde{{\pmb{\sigma}}}_u) + 2\lambda \mu ( \widetilde{{\pmb{\sigma}}}_u \cdot \widetilde{{\pmb{\sigma}}}_v) + \mu^2 ( \widetilde{{\pmb{\sigma}}}_v \cdot \widetilde{{\pmb{\sigma}}}_v) \\ & = (\lambda \widetilde{{\pmb{\sigma}}}_u + \mu \widetilde{{\pmb{\sigma}}}_v) \cdot (\lambda \widetilde{{\pmb{\sigma}}}_u + \mu \widetilde{{\pmb{\sigma}}}_v) \\ & = d_{\mathbf{p}} f (\mathbf{v}) \cdot d_{\mathbf{p}} f (\mathbf{v}) \,, \end{align*}\] showing that \[ \mathbf{v}\cdot \mathbf{v}= d_{\mathbf{p}} f (\mathbf{v}) \cdot d_{\mathbf{p}} f (\mathbf{v}) \,, \quad \forall \, \mathbf{v}\in T_{\mathbf{p}} \mathcal{S}\,. \] By Remark 112 we conclude that \(f\) is a local isometry.
4.11.4 Angles on surfaces
We want to define the notion of angle between tangent vectors.
Definition 115: Angle between tangent vectors
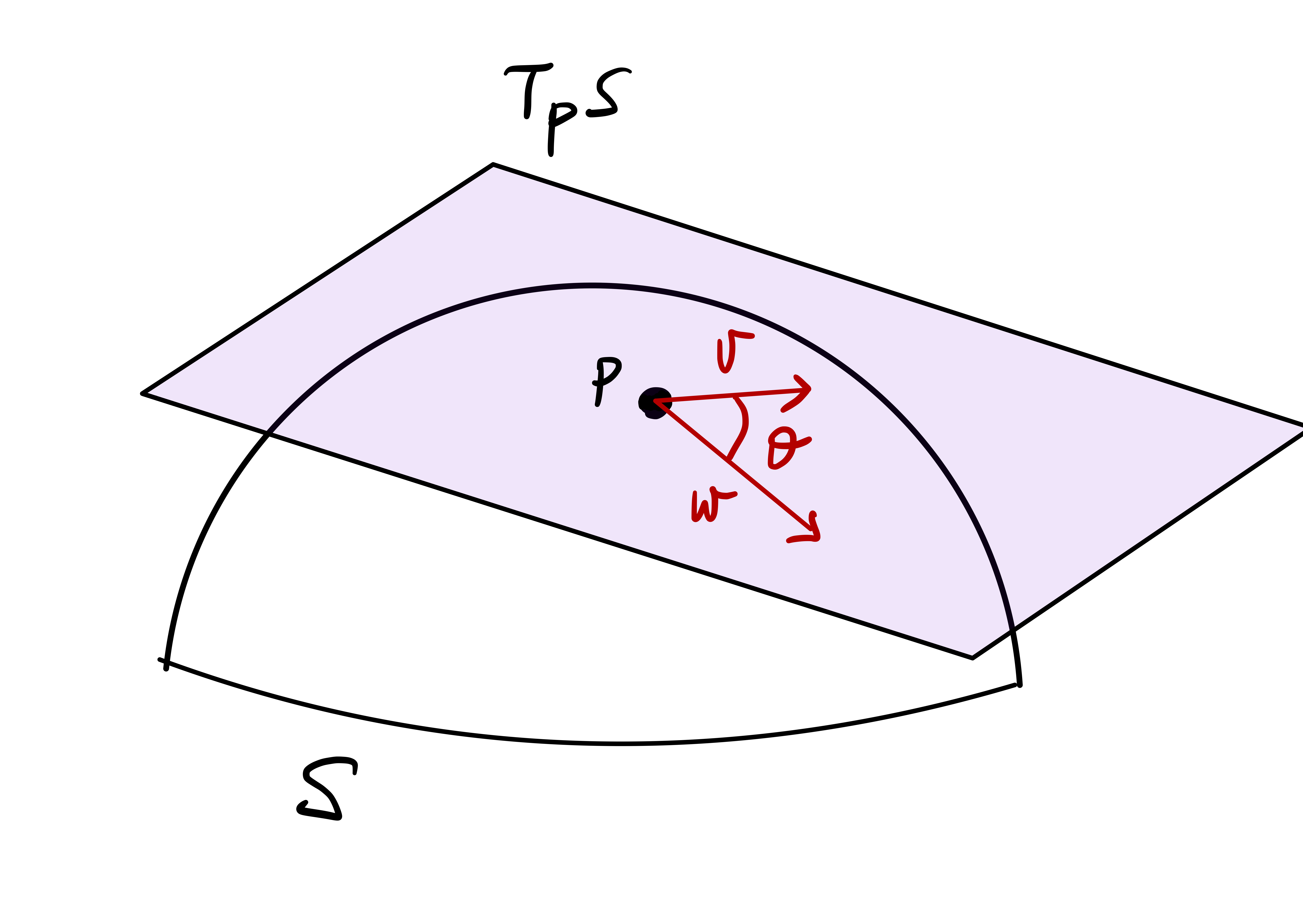
The angle between tangent vectors can be computed in terms of local charts.
Proposition 116
Proof
4.11.5 Angle between curves
Since tangent vectors are derivatives of curves with values in \(\mathcal{S}\), it also makes sense to define the angle between two intersecting curves.
Definition 117: Angle between curves
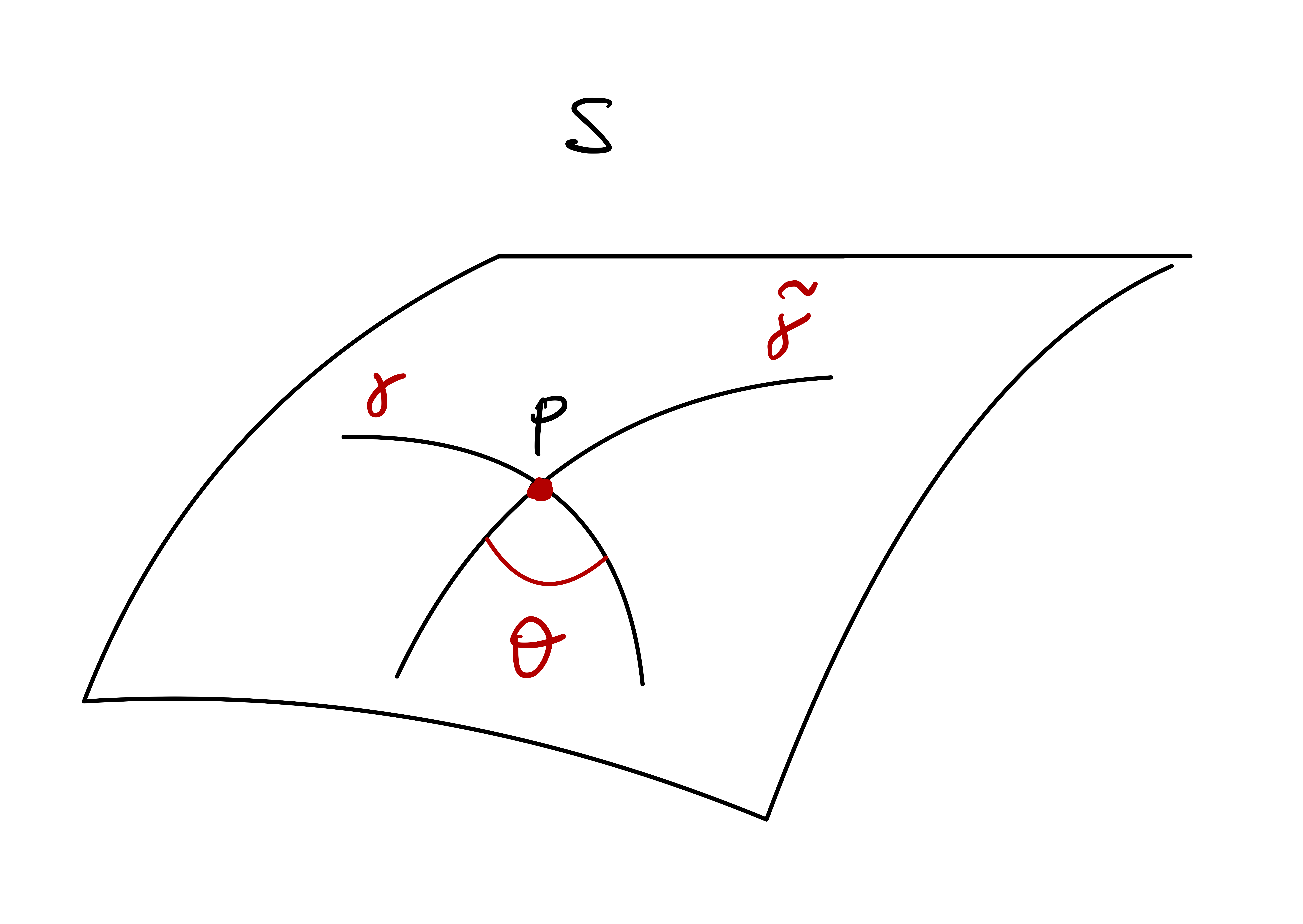
Proposition 118
Proof
4.11.6 Conformal maps
Local isometries are maps which preserve the scalar product of tangent vectors. We want to consider maps which preserve the angle of tangent vectors. These will be called conformal maps.
Definition 119: Conformal map
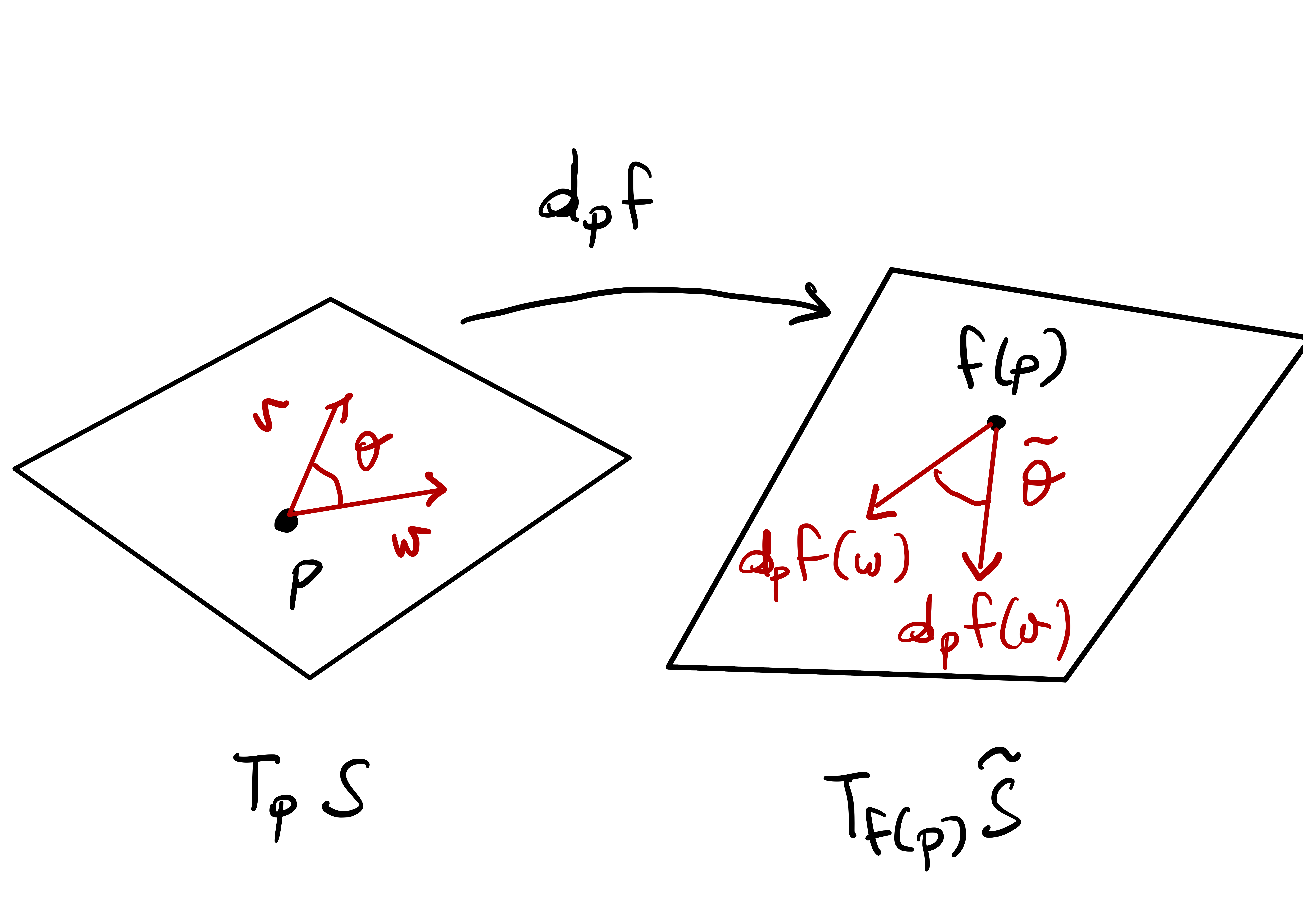
Remark 120
We have that \(f\) is a conformal map if and only if \[ \frac{ \left\langle \mathbf{v},\mathbf{w} \right\rangle }{ \| \mathbf{v}\| \, \| \mathbf{w}\| } = \frac{ \left\langle \mathbf{v},\mathbf{w} \right\rangle_f }{ \| \mathbf{v}\|_f \, \| \mathbf{w}\|_f } \,, \quad \forall \, \mathbf{v}, \mathbf{w}\in T_{\mathbf{p}} \mathcal{S}\,. \]
This follows immediately by the definition of angle between tangent vectors.
Proposition 121
Proof
Therefore every local isometry is a conformal map. The converse is false, as we will show in Example 124 below. Before giving the example, let us provide a characterization of conformal maps in terms of the first fundamental form.
Theorem 122
Let \(\mathcal{S}\) and \(\widetilde{\mathcal{S}}\) be regular surfaces and \(f \colon \mathcal{S}\to \widetilde{\mathcal{S}}\) a local diffeomorphism. They are equivalent:
- \(f\) is a conformal map.
- There exists a function \(\lambda \colon \mathcal{S}\to \mathbb{R}\) such that \[ \left\langle \mathbf{v},\mathbf{w} \right\rangle_f = \lambda (\mathbf{p}) \, \left\langle \mathbf{v},\mathbf{w} \right\rangle \,, \quad \forall \, \mathbf{v},\mathbf{w}\in T_{\mathbf{p}} \mathcal{S}\,. \]
Proof
Step 2. Suppose that there exists a function \(\lambda \colon \mathcal{S}\to \mathbb{R}\) such that \[ \left\langle \mathbf{v},\mathbf{w} \right\rangle_f = \lambda (\mathbf{p}) \, \left\langle \mathbf{v},\mathbf{w} \right\rangle \,, \quad \forall \, \mathbf{v},\mathbf{w}\in T_{\mathbf{p}} \mathcal{S}\,. \] In particular, we have \[ \| \mathbf{v}\|_f = \sqrt{\lambda(\mathbf{p})} \| \mathbf{v}\| \,, \quad \forall \, \mathbf{v}\in T_{\mathbf{p}} \mathcal{S}\,. \] Then \[ \frac{\left\langle \mathbf{v},\mathbf{w} \right\rangle_f}{ \| \mathbf{v}\|_f \| \mathbf{w}\|_f } = \frac{\lambda (\mathbf{p}) \, \left\langle \mathbf{v},\mathbf{w} \right\rangle}{ \sqrt{\lambda(\mathbf{p})} \| \mathbf{v}\| \sqrt{\lambda(\mathbf{p})} \| \mathbf{w}\| } = \frac{\left\langle \mathbf{v},\mathbf{w} \right\rangle}{ \| \mathbf{v}\| \| \mathbf{w}\| } \,, \] showing that \(f\) is a conformal map.
Corollary 123
Let \(\mathcal{S}\) and \(\widetilde{\mathcal{S}}\) be regular surfaces and \(f \colon \mathcal{S}\to \widetilde{\mathcal{S}}\) be a local diffeomorphism. They are equivalent:
- \(f\) is a conformal map.
- Let \({\pmb{\sigma}}\colon U \to \mathcal{S}\) be a regular chart of \(\mathcal{S}\) and consider the chart of \(\widetilde{\mathcal{S}}\) given by \[ \widetilde{{\pmb{\sigma}}} = f \circ {\pmb{\sigma}}\colon U \to \widetilde{\mathcal{S}} \,. \] There exists \(\lambda \colon U \to \mathbb{R}\) such that \[ \widetilde{\mathscr{F}}_1 = \lambda (u,v) \mathscr{F}_1 \,, \quad \forall \, (u,v) \in U \,, \] where \(\mathscr{F}_1\) and \(\widetilde{\mathscr{F}}_1\) are the first fundamental forms of \({\pmb{\sigma}}\) and \(\widetilde{{\pmb{\sigma}}}\), respectively.
The follows by using Theorem 122, and by adapting the argument in the proof of Theorem 114.
Example 124: Conformal maps are not local isometries
Consider the plane \(\mathcal{S}\) with chart \[ {\pmb{\sigma}}(u,v) := (u,v,0) \,. \] Let \(\widetilde{\mathcal{S}}\) be the sphere with parametrization \[ \widetilde{{\pmb{\sigma}}}(u,v) := \left( \mathop{\mathrm{sech}}(u) \cos(v), \mathop{\mathrm{sech}}(u) \sin(v) , \tanh (u) \right) \,. \] We have \[ {\pmb{\sigma}}_u = (1,0,0) \,, \quad {\pmb{\sigma}}_v = (0,1,0) \,, \] so that \[\begin{align*} E & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_u = 1 \\ F & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v = 0 \\ G & = {\pmb{\sigma}}_v \cdot {\pmb{\sigma}}_v = 1 \\ \end{align*}\] Therefore the first fundamental form of \(\mathcal{S}\) is \[ \mathscr{F}_1 = du^2 + dv^2 \,. \] Using the identitities \[\begin{align*} \frac{d}{du} \left( \mathop{\mathrm{sech}}(u) \right) & = - \mathop{\mathrm{sech}}(u) \tanh (u) \,, \\ \frac{d}{du} \left( \tanh (u) \right) & = {\mathop{\mathrm{sech}}}^2 (u) \,, \end{align*}\] we obtain \[\begin{align*} \widetilde{{\pmb{\sigma}}}_u & = ( -\mathop{\mathrm{sech}}(u) \tanh(u) \cos(v), -\mathop{\mathrm{sech}}(u) \tanh(u) \sin(v), {\mathop{\mathrm{sech}}}^2(u) ) \\ \widetilde{{\pmb{\sigma}}}_v & = ( -\mathop{\mathrm{sech}}(u) \sin(v), \mathop{\mathrm{sech}}(u) \cos(v), 0 ) \end{align*}\] By recalling that \[ {\mathop{\mathrm{sech}}}^2 (u) + {\tanh}^2 (u) = 1 \,, \] we compute \[\begin{align*} \widetilde{E} & = \widetilde{{\pmb{\sigma}}}_u \cdot \widetilde{{\pmb{\sigma}}}_u = {\mathop{\mathrm{sech}}}^2(u) ({\tanh}^2(u) + {\mathop{\mathrm{sech}}}^2(u)) = {\mathop{\mathrm{sech}}}^2(u) \\ \widetilde{F} & = \widetilde{{\pmb{\sigma}}}_u \cdot \widetilde{{\pmb{\sigma}}}_v = 0 \\ \widetilde{G} & = \widetilde{{\pmb{\sigma}}}_v \cdot \widetilde{{\pmb{\sigma}}}_v = {\mathop{\mathrm{sech}}}^2(u) (\cos^2(v) + \sin^2(v)) = {\mathop{\mathrm{sech}}}^2(u) \\ \end{align*}\] Hence the first fundamental form of \(\widetilde{\mathcal{S}}\) is \[ \widetilde{\mathscr{F}}_1 = {\mathop{\mathrm{sech}}}^2(u) \, \left( du^2 + dv^2 \right) \,. \] Now, consider the map \(f \colon \mathcal{S}\to \widetilde{\mathcal{S}}\) defined by \[ f(u,v,0) = \widetilde{{\pmb{\sigma}}} (u,v) \,. \] In particular \(f\) satisfies \[ f( {\pmb{\sigma}}( u,v) ) = \widetilde{{\pmb{\sigma}}} (u,v) \,. \] We have:
- \(f\) is not a local isometry.
If \(f\) was a local isometry, by Theorem 114 we would conclude that \({\pmb{\sigma}}\) and \(\widetilde{{\pmb{\sigma}}} = f \circ {\pmb{\sigma}}\) have the same first fundamental form. However \[ \mathscr{F}_1 = du^2 + dv^2 \neq {\mathop{\mathrm{sech}}}^2(u) \, \left( du^2 + dv^2 \right) = \widetilde{\mathscr{F}}_1 \,. \]
- \(f\) is a conformal map.
The first fundamental forms of \({\pmb{\sigma}}\) and \(\widetilde{{\pmb{\sigma}}} = f \circ {\pmb{\sigma}}\) satisfy \[ \widetilde{\mathscr{F}}_1 = \lambda(u,v) \, \mathscr{F}_1 \,, \quad \lambda(u,v) := {\mathop{\mathrm{sech}}}(u) \,. \] Therefore \(f\) is a conformal map by Corollary 123.
4.11.7 Conformal parametrizations
We conclude this section with the definition of conformally flat surface and conformal parametrization.
Definition 125: Conformally flat surface and conformal parametrization
Definition 125 is motivated by the following Theorem: It states that angles on conformally flat surfaces look like angles on a plane.
Theorem 126
Let \(\mathcal{S}\) be a regular surface and \[ {\pmb{\sigma}}\colon U \to {\pmb{\sigma}}(U) \subseteq \mathcal{S} \] be a regular chart of \(\mathcal{S}\). Define the plane \({\pmb{\pi}}\) charted by \[ \widetilde{{\pmb{\sigma}}} (u,v) = (u,v,0) \,, \quad \forall \, (u,v) \in U \,. \]
They are equivalent:
\({\pmb{\sigma}}\) is a conformal parametrization.
There exists a conformal map \(f \colon \pi \to {\pmb{\sigma}}(U) \subseteq \mathcal{S}\).
A conformal parametrization \({\pmb{\sigma}}\) preserves angles between vectors, in the following sense: Suppose \({\pmb{\gamma}}_1, {\pmb{\gamma}}_2\) are curves in \(\mathbb{R}^{2}\) such that \[ {\pmb{\gamma}}_1 (t_0) = {\pmb{\gamma}}_2 (t_0) \,. \] Consider the corresponding curves on \(\mathcal{S}\) given by \[ \widetilde{{\pmb{\gamma}}}_1 := {\pmb{\sigma}}\circ {\pmb{\gamma}}_1 \,, \quad \widetilde{{\pmb{\gamma}}}_2 = {\pmb{\sigma}}\circ {\pmb{\gamma}}_2 \,. \] If \[ \dot{{\pmb{\gamma}}}_1 (t_0) \,, \dot{{\pmb{\gamma}}}_2(t_0) \,\, \mbox{ form an angle } \,\, \theta \,, \] then \[ \dot{\widetilde{{\pmb{\gamma}}}}_1 (t_0) \,, \dot{\widetilde{{\pmb{\gamma}}}}_2(t_0) \,\, \mbox{ form an angle } \,\, \theta \,. \]
Proof
Proof of Point 2. Suppose \({\pmb{\sigma}}\) is a conformal parametrization. By the proof of Point 1 we have that \[ f \colon \pi \to \mathcal{S}\,, \quad f(u,v,0) = {\pmb{\sigma}}(u,v) \,, \] is a conformal map. Since \(T_{\mathbf{p}} \pi = \mathbb{R}^2\) and \(f = {\pmb{\sigma}}\), it follows by the definition of differential and \(f\) being conformal that the angle between \({\pmb{\gamma}}_1\) and \({\pmb{\gamma}}_2\) is the same as the angle between \(\widetilde{{\pmb{\gamma}}}_1\) and \(\widetilde{{\pmb{\gamma}}}_2\).
Example 127: Unit cylinder
Example 128: Shpere
4.12 Second fudamental form
The first fundamental form allows to measure distances on a surface. However it does not give any information on how curved a surface is: For example, we saw that a plane and a cylinder have the same first fundamental form \[ \mathscr{F}_1 = du^2 + dv^2 \,. \] However the plane is flat, while the cylinder curves. We would like to find a measure of curvature which allows us to tell these two surfaces apart.
4.12.1 Unit normal and orientability
Before talking about curvatures, we need to clarify what we mean by normal vector to a surface and orientability. Let \(\mathcal{S}\) be a regular surface and \(\mathbf{p}\in \mathcal{S}\). The tangent plane \(T_{\mathbf{p}} \mathcal{S}\) passes through the origin. Therefore \(T_{\mathbf{p}} \mathcal{S}\) is completely determined by giving a unit vector \(\mathbf{N}\) perpendicular to it: \[ T_{\mathbf{p}} \mathcal{S}= \{ \mathbf{x}\in \mathbb{R}^3 \, \colon \,\mathbf{x}\cdot \mathbf{N}= 0 \} \,. \] In this case we write \[ \mathbf{N}\perp T_{\mathbf{p}} \mathcal{S}\,, \] to denote that \(\mathbf{N}\) is perpendicular to \(T_{\mathbf{p}} \mathcal{S}\). Clearly, also \(-\mathbf{N}\) is a unit vector, and \[ (- \mathbf{N}) \perp T_{\mathbf{p}} \mathcal{S}\,. \]
Question 129
There is no right answer to the above question. One way to proceed is the following.
Remark 130
There is however an issue: \(\mathbf{N}_{{\pmb{\sigma}}}\) is not independent on the choice of chart \({\pmb{\sigma}}\). Indeed, suppose that \(\widetilde{{\pmb{\sigma}}} \colon \widetilde{U} \to \mathbb{R}^3\) is a reparametrization of \({\pmb{\sigma}}\), that is, \[ \widetilde{{\pmb{\sigma}}} = {\pmb{\sigma}}\circ \Phi \,, \quad \Phi \colon \widetilde{U} \to U \,, \] with \(\Phi\) diffeomorphism. As shown in the proof of Proposition 61, we have \[ \widetilde{{\pmb{\sigma}}}_{\tilde{u}} \times \widetilde{{\pmb{\sigma}}}_{\tilde{v}} = \det (J\Phi) \, {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \,. \] Hence \[ \mathbf{N}_{\widetilde{{\pmb{\sigma}}}} = \frac{ \widetilde{{\pmb{\sigma}}}_{\tilde{u}} \times \widetilde{{\pmb{\sigma}}}_{\tilde{v}} }{\left\| \widetilde{{\pmb{\sigma}}}_{\tilde{u}} \times \widetilde{{\pmb{\sigma}}}_{\tilde{v}} \right\|} = \frac{\det J\Phi}{|\det J\Phi|} \frac{{\pmb{\sigma}}_u \times {\pmb{\sigma}}_v}{\left\| {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \right\|} = \pm \mathbf{N}_{{\pmb{\sigma}}} \,. \] Therefore the sign on the right hand side depends on the sign of the Jacobian determinant of the transition map \(\Phi\).
The above remark motivates the following definitions.
Definition 131: Standard unit normal of a chart
Definition 132: Charts with same orientation
Let \(\mathcal{S}\) be a regular surface and \({\pmb{\sigma}}\colon U \to \mathbb{R}^3\), \(\widetilde{{\pmb{\sigma}}} \colon \widetilde{U} \to \mathbb{R}^3\) regular charts such that \[ {\pmb{\sigma}}(U) \cap \widetilde{{\pmb{\sigma}}} (\widetilde{U}) \neq \emptyset \,. \] Denote by \(\Phi\) the transition map between \(\widetilde{{\pmb{\sigma}}}\) and \({\pmb{\sigma}}\). We say that:
\({\pmb{\sigma}}\) and \(\widetilde{{\pmb{\sigma}}}\) determine the same orientation if \[ \det J \Phi > 0 \,, \] where \(\Phi\) is defined.
\({\pmb{\sigma}}\) and \(\widetilde{{\pmb{\sigma}}}\) determine opposite orientations if \[ \det J \Phi < 0 \,, \] where \(\Phi\) is defined.
Example 133
If a surface can be covered by charts with the same orientation, it is called orientable.
Definition 134: Orientable surface
Let \(\mathcal{S}\) be a regular surface. Then:
An atlas \(\mathcal{A} = \{ {\pmb{\sigma}}_i \}_{i \in I}\) is oriented if the following property holds: \[ {\pmb{\sigma}}_i (U_i) \cap {\pmb{\sigma}}_j (U_j) \neq \emptyset \quad \implies \quad \det J \Phi > 0 \,, \] where \(\Phi\) is the transition map between \({\pmb{\sigma}}_i\) and \({\pmb{\sigma}}_j\).
\(\mathcal{S}\) is orientable if there exists an oriented atlas \(\mathcal{A}\).
If an oriented atlas \(\mathcal{A}\) is assigned, we say that \(\mathcal{S}\) is oriented by \(\mathcal{A}\).
Example 135
Example 136
Let \({\pmb{\sigma}}\colon U \to \mathbb{R}^3\) be a regular chart. Then \[ \mathcal{S}_{{\pmb{\sigma}}} := {\pmb{\sigma}}(U) \] is a regular surface with atlas \(\mathcal{A}=\{{\pmb{\sigma}}\}\). Therefore \(\mathcal{S}_{{\pmb{\sigma}}}\) is orientable.
This is because we have only one chart. Therefore any transition map \(\Phi\) will be the identity, so that \(\det J \Phi = 1 > 0\).
Warning: Orientability is a global property
Remark 137
Definition 138: Unit normal of a surface
Warning
Proposition 139
Let \(\mathcal{S}\) be a regular surface. They are equivalent:
\(\mathcal{S}\) is orientable.
There exists a unit normal \(\mathbf{N}\colon \mathcal{S}\to \mathbb{R}^3\).
The proof follows from the above arguments. For details, we refer the reader to Proposition 4.3.7 in (Abate, Marco and Tovena, Francesca 2011).
In view of the above propostion, for an oriented surface there is a natural choice of unit normal, which we call standard unit normal of \(\mathcal{S}\).
Definition 140: Standard unit normal of a surface
Notation
4.12.2 Definition of Second fundamental form
We can now start our discussion about curvature of surfaces. We can make a similar argument to the one we made for curves: If \({\pmb{\gamma}}\) is a unit speed curve, the curvature of \({\pmb{\gamma}}\) is defined as \[ \kappa (t) = \left\| \ddot{{\pmb{\gamma}}}(t) \right\| \,. \] The quantity \(\kappa(t)\) gave us a measure of how much \({\pmb{\gamma}}\) is deviating from a straight line. Similarly, we would like to quantify how much a surface \(\mathcal{S}\) is deviating from the tangent plane \(T_{\mathbf{p}} \mathcal{S}\). Recall that \[ T_{\mathbf{p}} \mathcal{S}= \operatorname{span} \{ {\pmb{\sigma}}_u , {\pmb{\sigma}}_v \} \,, \] where \({\pmb{\sigma}}\) is a regular chart of \(\mathcal{S}\) at \(\mathbf{p}\). The standard unit normal of \({\pmb{\sigma}}\) is \[ \mathbf{N}= \frac{ {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v }{ \left\| {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \right\| } \,, \] which is orthogonal to \(T_{\mathbf{p}} \mathcal{S}\). Let \((u_0,v_0) \in \mathbb{R}^2\) be the point such that \[ {\pmb{\sigma}}(u_0,v_0) = \mathbf{p}\,. \] As the scalar quantities \(\Delta u\) and \(\Delta v\) vary, the point \[ {\pmb{\sigma}}( u_0 + \Delta u , v_0 + \Delta v ) \in \mathcal{S} \] deviates from the tangent plane \(T_{\mathbf{p}} \mathcal{S}\). Since \(\mathbf{N}\) is orthogonal to \(T_{\mathbf{p}} \mathcal{S}\), the deviation is given by \[ \delta := \left[ {\pmb{\sigma}}( u_0 + \Delta u , v_0 + \Delta v ) - {\pmb{\sigma}}(u_0,v_0) \right] \cdot \mathbf{N}\,, \] as shown in Figure 4.10.
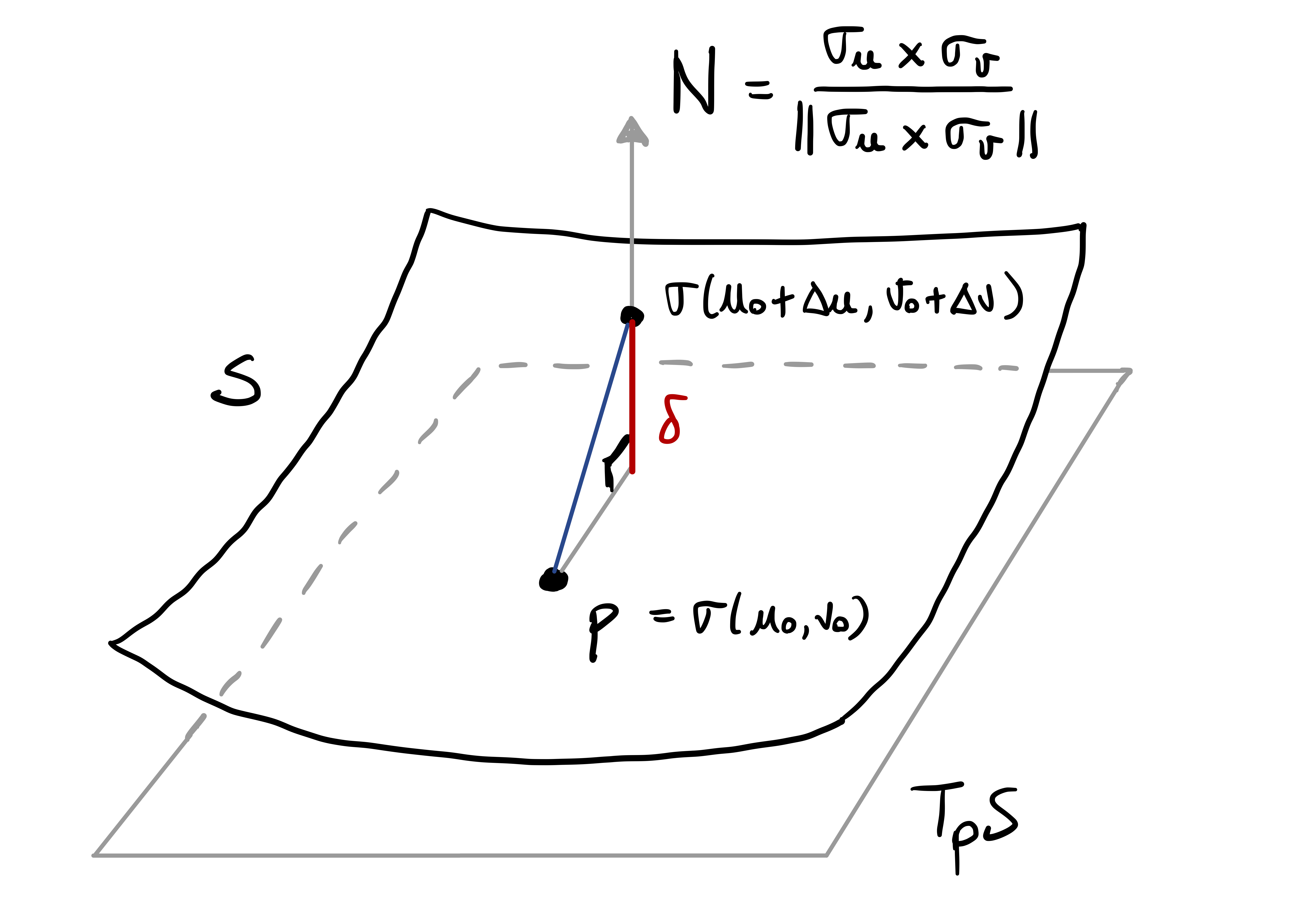
Using Taylor’s formula we get \[\begin{align*} {\pmb{\sigma}}(u_0 + \Delta u , v_0 + \Delta v) & = {\pmb{\sigma}}(u_0,v_0) + {\pmb{\sigma}}_u (u_0,v_0) \, \Delta u + {\pmb{\sigma}}_v (u_0,v_0) \, \Delta v \\ & \,\, + \frac12 \left( {\pmb{\sigma}}_{uu}(u_0,v_0) (\Delta u)^2 + 2 {\pmb{\sigma}}_{uv}(u_0,v_0) \Delta u \Delta v +{{\pmb{\sigma}}}_{vv}(u_0,v_0) (\Delta v)^2 \right) \\ & \,\, + R(\Delta u , \Delta v) \,, \end{align*}\] where \(R(\Delta u , \Delta v)\) is a remainder such that \[ \lim_{\Delta \to 0} \, \frac{R(\Delta u , \Delta v) }{\Delta } = 0 \,, \quad \Delta := (\Delta u)^2 + (\Delta v)^2 \,. \] Since \(\mathbf{N}\) is orthogonal to \({\pmb{\sigma}}_u\) and \({\pmb{\sigma}}_v\), if we multiply the above Taylor expansion by \(\mathbf{N}\), and ignore the remainder, we obtain \[ \delta = \frac12 \left( L (\Delta u)^2 + 2 M \Delta u \Delta v + N (\Delta v)^2 \right) \,, \] where we set \[ L := {\pmb{\sigma}}_{uu} \cdot \mathbf{N}\,, \quad M := {\pmb{\sigma}}_{uv} \cdot \mathbf{N}\,, \quad N := {\pmb{\sigma}}_{vv} \cdot \mathbf{N}\,. \] The expression \[ \mathscr{F}_2 := L \, du^2 + 2 M \,du dv + N \, dv^2 \] is called the second fundamental form of \(\mathcal{S}\). Therefore \(\mathscr{F}_2\) measures how much the surface \(\mathcal{S}\) deviates from being a plane. Let us make this definition precise.
Definition 141: Second fundamental form of a chart
Notation
Remark 142: Second fundamental form and reparametrizations
The second fundamental form \[ \mathscr{F}_2 = L \, du^2 + 2M \, du dv + N \, dv^2 \] depends on the choice of chart \({\pmb{\sigma}}\colon U \to \mathbb{R}^3\). Indeed, let us adopt the same notations as Remark 105. Suppose that \(\widetilde{{\pmb{\sigma}}} \colon \widetilde{U} \to \mathbb{R}^3\) is a reparametrization of \({\pmb{\sigma}}\) with \[ \widetilde{{\pmb{\sigma}}} = {\pmb{\sigma}}\circ \Phi \,, \] where \(\Phi \colon \widetilde{U} \to U\) is a diffeomorphism. Denote the second fundamental form of \(\widetilde{{\pmb{\sigma}}}\) by \[ \widetilde{\mathscr{F}}_2 = \widetilde{L} \, d\tilde{u}^2 + 2 \widetilde{M} \, d\tilde{u} d\tilde{v} + \widetilde{N} \, d\tilde{v}^2 \,. \] The matrices of \(\mathscr{F}_2\) and \(\widetilde{\mathscr{F}}_2\) are related by \[ \left( \begin{array}{cc} \widetilde{L} & \widetilde{M} \\ \widetilde{M} & \widetilde{N} \end{array} \right) = \pm (J \Phi)^T \, \left( \begin{array}{cc} L & M \\ M & N \end{array} \right) \, J \Phi \,, \tag{4.10}\] where (4.10) holds with \(+\) if \(\det J\Phi > 0\) and \(-\) if \(\det J\Phi < 0\).
Formula (4.10) holds by a change of variable argument. The sign depends on the sign of \(\det J\Phi\) because \[ \widetilde{\mathbf{N}} = \frac{ \widetilde{{\pmb{\sigma}}}_{\tilde{u}} \times \widetilde{{\pmb{\sigma}}}_{\tilde{v}} }{\left\| \widetilde{{\pmb{\sigma}}}_{\tilde{u}} \times \widetilde{{\pmb{\sigma}}}_{\tilde{v}} \right\|} = \frac{\det J\Phi}{|\det J\Phi|} \frac{{\pmb{\sigma}}_u \times {\pmb{\sigma}}_v}{\left\| {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \right\|} = \pm \mathbf{N}\,, \] as shown in Remark 130.
Let us show that a plane and a cylinder have different second fundamental forms.
Example 143: Plane
Let \(\mathbf{a}, \mathbf{p}, \mathbf{q} \in \mathbb{R}^3\). Suppose that \(\mathbf{p}\) and \(\mathbf{q}\) are orthonormal vectors, that is, \[ \left\| \mathbf{p} \right\| = \left\| \mathbf{q} \right\| = 1 \,, \quad \mathbf{p}\cdot \mathbf{q} = 0 \,. \] Consider the plane with chart \[ {\pmb{\sigma}}(u,v) = \mathbf{a} + u \mathbf{p}+ v \mathbf{q} \,, \quad (u,v) \in \mathbb{R}^2 \,. \] Prove that the second fundamental form of \({\pmb{\sigma}}\) is \[ \mathscr{F}_2 = 0 \,. \] This reflects the intuition that a plane is flat, and therefore there is no curvature.
We have \[ {\pmb{\sigma}}_u = \mathbf{p}\,, \quad {\pmb{\sigma}}_v = \mathbf{q} \,. \] The principal unit normal is \[ \mathbf{N}= \frac{\mathbf{p}\times \mathbf{q}}{\left\| \mathbf{p}\times \mathbf{q} \right\| } \,, \] while the second derivatives are \[ {\pmb{\sigma}}_{\mathbf{u}} = {\pmb{\sigma}}_{\mathbf{u}} = {\pmb{\sigma}}_{\mathbf{u}} = {\pmb{0}}\,. \] Therefore \[\begin{align*} L & = {\pmb{\sigma}}_{uu} \cdot \mathbf{N}= 0 \\ M & = {\pmb{\sigma}}_{uv} \cdot \mathbf{N}= 0 \\ N & = {\pmb{\sigma}}_{vv} \cdot \mathbf{N}= 0 \\ \end{align*}\] and the second fundamental form is \[ \mathscr{F}_2 = L \, du^2 + 2 M\, du \, dv + N \, dv^2 = 0 \,. \]
Example 144: Unit cylinder
Consider the unit cylinder with chart \[ {\pmb{\sigma}}(u,v) = (\cos(u), \sin(u), v) \,, \quad (u,v) \in (0,2\pi) \times \mathbb{R}\,. \] Prove that the second fundamental form of \({\pmb{\sigma}}\) is \[ \mathscr{F}_2 = - du^2 \,. \] This reflects the intuition that the cylinder curves only when moving in the \(v\)-direction. In such direction we are moving on a circle of radius \(1\), therefore we expect the curvature to be \(-1\).
We have \[ {\pmb{\sigma}}_u = (-\sin(u),\cos(u), 0 ) \,, \quad {\pmb{\sigma}}_v = (0,0,1) \,, \] and also \[ {\pmb{\sigma}}_{uu} = (-\cos(u), - \sin(u), 0 ) \,, \quad {\pmb{\sigma}}_{uv} = {\pmb{\sigma}}_{vv} = {\pmb{0}}\,. \] We have also \[ {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v = \left| \begin{array}{ccc} \mathbf{i}& \mathbf{j}& \mathbf{k}\\ -\sin(u) & \cos(u) & 0 \\ 0 & 0 & 1 \end{array} \right| = (\cos(u), \sin(u),0) \] so that \[ \left\| {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \right\| = \sqrt{ \cos^2(u) + \sin^2(u) } = 1 \,. \] The principal unit normal is \[ \mathbf{N}= \frac{{\pmb{\sigma}}_u \times {\pmb{\sigma}}_v}{ \left\| {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \right\| } = (\cos(u), \sin(u),0) \,. \] We finally compute \[\begin{align*} L & = {\pmb{\sigma}}_{uu} \cdot \mathbf{N}\\ & = (-\cos(u), - \sin(u), 0 ) \cdot (\cos(u), \sin(u),0) \\ & = - \cos^2(u) - \sin^2(u) = - 1 \\ M & = {\pmb{\sigma}}_{uv} \cdot \mathbf{N}= 0 \\ N & = {\pmb{\sigma}}_{vv} \cdot \mathbf{N}= 0 \\ \end{align*}\] The second fundamental form is \[ \mathscr{F}_2 = L \, du^2 + 2 M\, du \, dv + N \, dv^2 = - du^2 \,. \]
Remark 145
4.12.3 Gauss and Weingarten maps
Another way to quantify how much a surface \(\mathcal{S}\) is curving is by examining the behavior of standard unit normal \(\mathbf{N}\). If \(\mathcal{S}\) is a plane spanned by vectors \(\mathbf{p}\) and \(\mathbf{q}\), then its standard unit normal is \[ \mathbf{N}= \frac{\mathbf{p}\times \mathbf{q}}{ \left\| \mathbf{p}\times \mathbf{q} \right\| } \,, \] which is constant across \(\mathcal{S}\). If \(\mathcal{S}\) is a general surface, measuring the variation of \(\mathbf{N}\) will tell us how much \(\mathcal{S}\) is deviating from being a plane. This is the idea behind the definition of the Gauss and Weingarten maps.
Remark 146
Definition 147: Gauss map
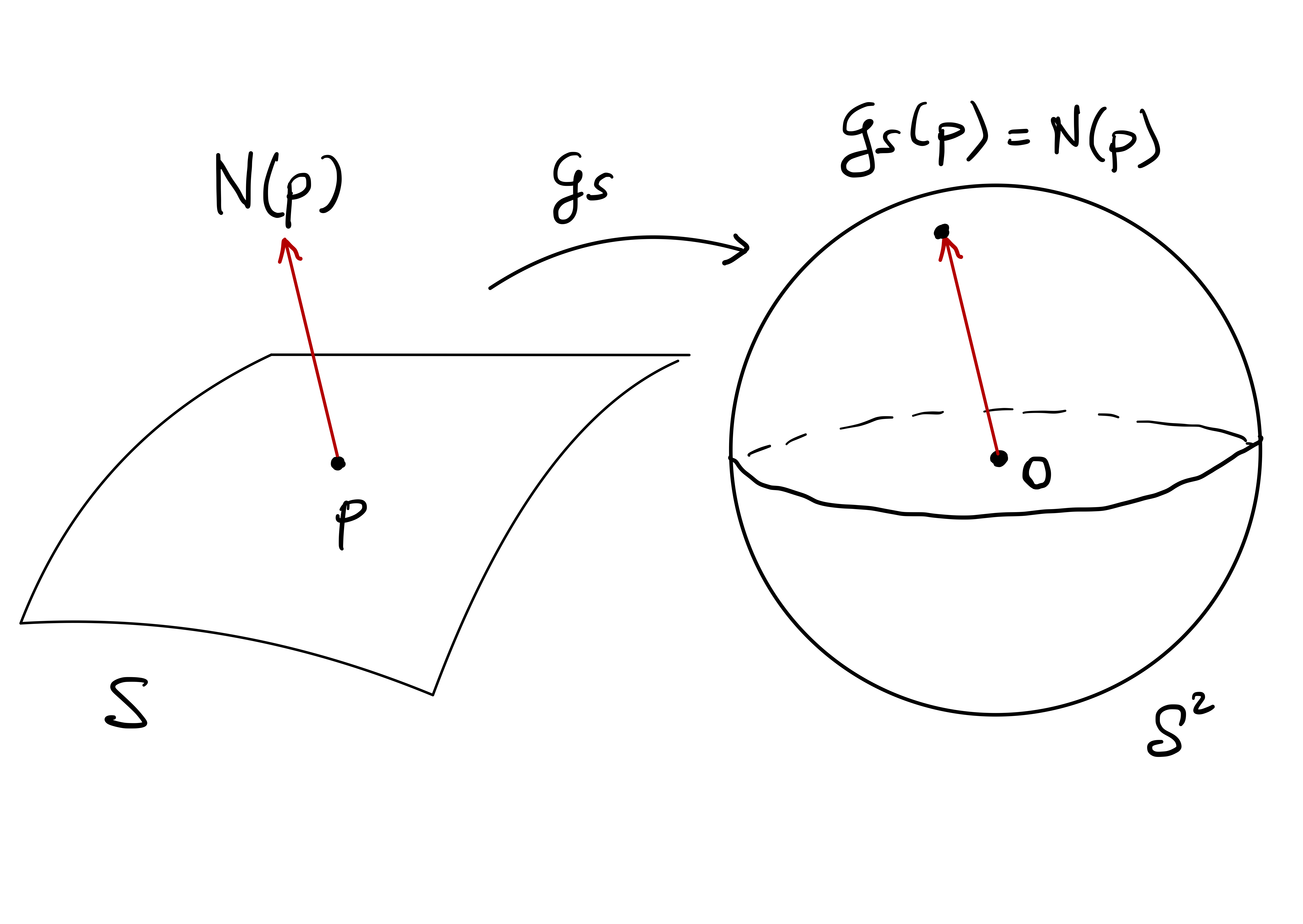
Remark 148
Example 149
Suppose \(\mathcal{S}\) is the unit sphere \(\mathbb{S}^2\). Then \({\mathcal{G}}_{\mathcal{S}} \colon \mathcal{S}\to \mathbb{S}^2\) is the identity, see Figure 4.11.
Let \(\mathbf{a} , \mathbf{v},\mathbf{w}\in \mathbb{R}^3\) with \(\mathbf{v}\) and \(\mathbf{w}\) linearly independent. Let \(\mathcal{S}\) be the plane \[ {\pmb{\sigma}}(u,v):= \mathbf{a} + \mathbf{v}u + \mathbf{\mathbf{w}} v \,, \quad \forall \, (u,v) \in \mathbb{R}^2 \,. \] The Gauss map of \(\mathcal{S}\) is constant: \[ \mathcal{G}_{\mathcal{S}} (\mathbf{p}) = \frac{ \mathbf{v}\times \mathbf{w}}{ \| \mathbf{v}\times \mathbf{w}\| } \,, \] for all \(\mathbf{p}\in \mathcal{S}\), see Figure 4.12.
Let \(\mathcal{S}\) be the unit cylinder \[ {\pmb{\sigma}}(u,v) = (\cos(u), \sin(u), v) \,, \quad (u,v) \in (0,2\pi) \times \mathbb{R}\,. \] Then \[ {\pmb{\sigma}}_u = (-\sin(u),\cos(u), 0 ) \,, \quad {\pmb{\sigma}}_v = (0,0,1) \,, \] and \[ {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v = \left| \begin{array}{ccc} \mathbf{i}& \mathbf{j}& \mathbf{k}\\ -\sin(u) & \cos(u) & 0 \\ 0 & 0 & 1 \end{array} \right| = (\cos(u), \sin(u), 0) \,. \] Therefore \[ \left\| {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \right\| = 1 \,, \] and \[ \mathbf{N}= \frac{ {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v }{ \left\| {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \right\| } = (\cos(u), \sin(u), 0) \,. \] The Gauss map of \(\mathcal{S}\) is \[ \mathcal{G}_{\mathcal{S}} (\mathbf{p}) = (\cos(u_0), \sin(u_0), 0) \,, \] where \((u_0,v_0)\) is such that \({\pmb{\sigma}}(u_0,v_0)=\mathbf{p}\). Note that \(\mathcal{G}_{\mathcal{S}}\) maps \(\mathcal{S}\) into the equator of \(\mathbb{S}^2\), see Figure 4.13.
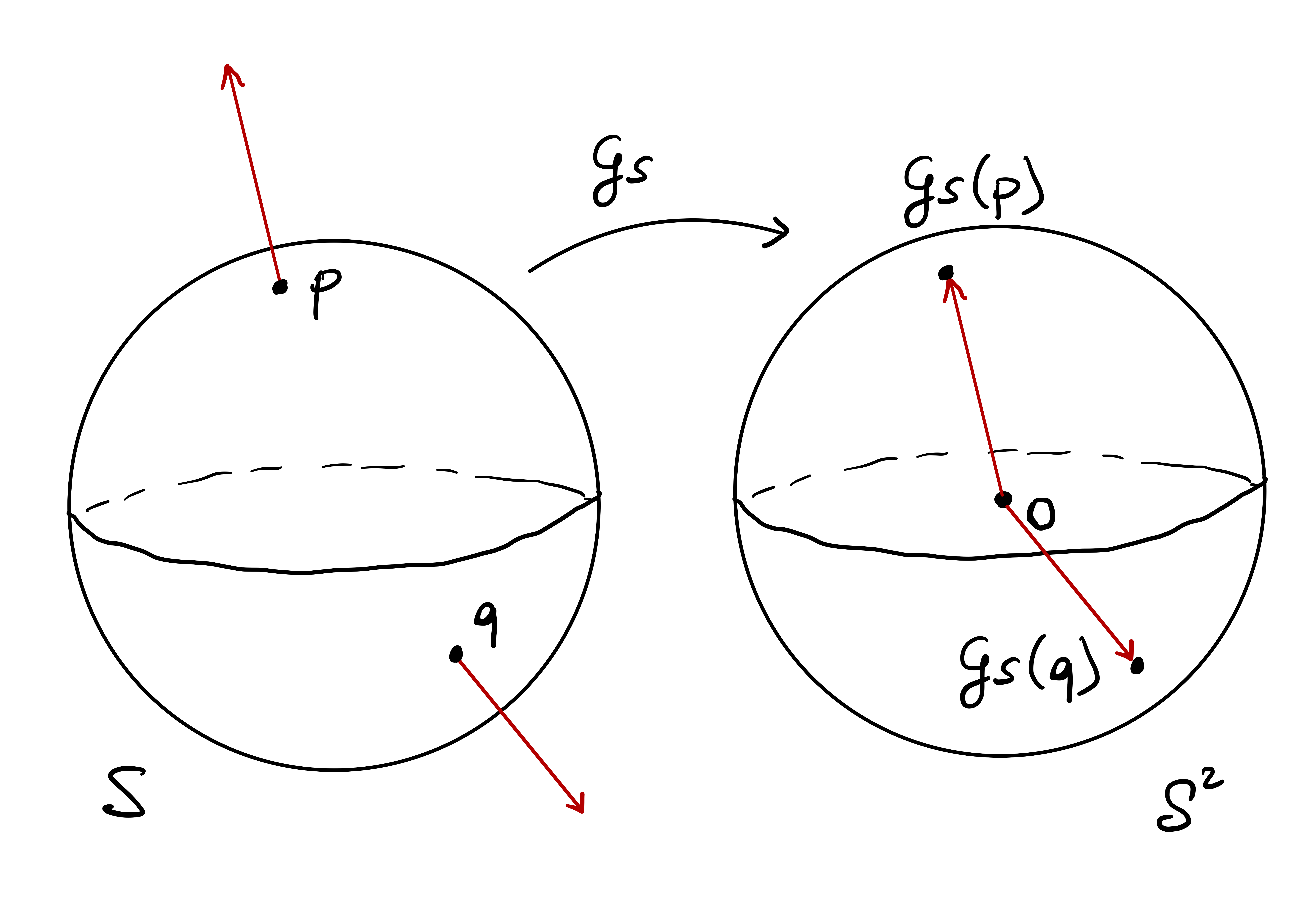
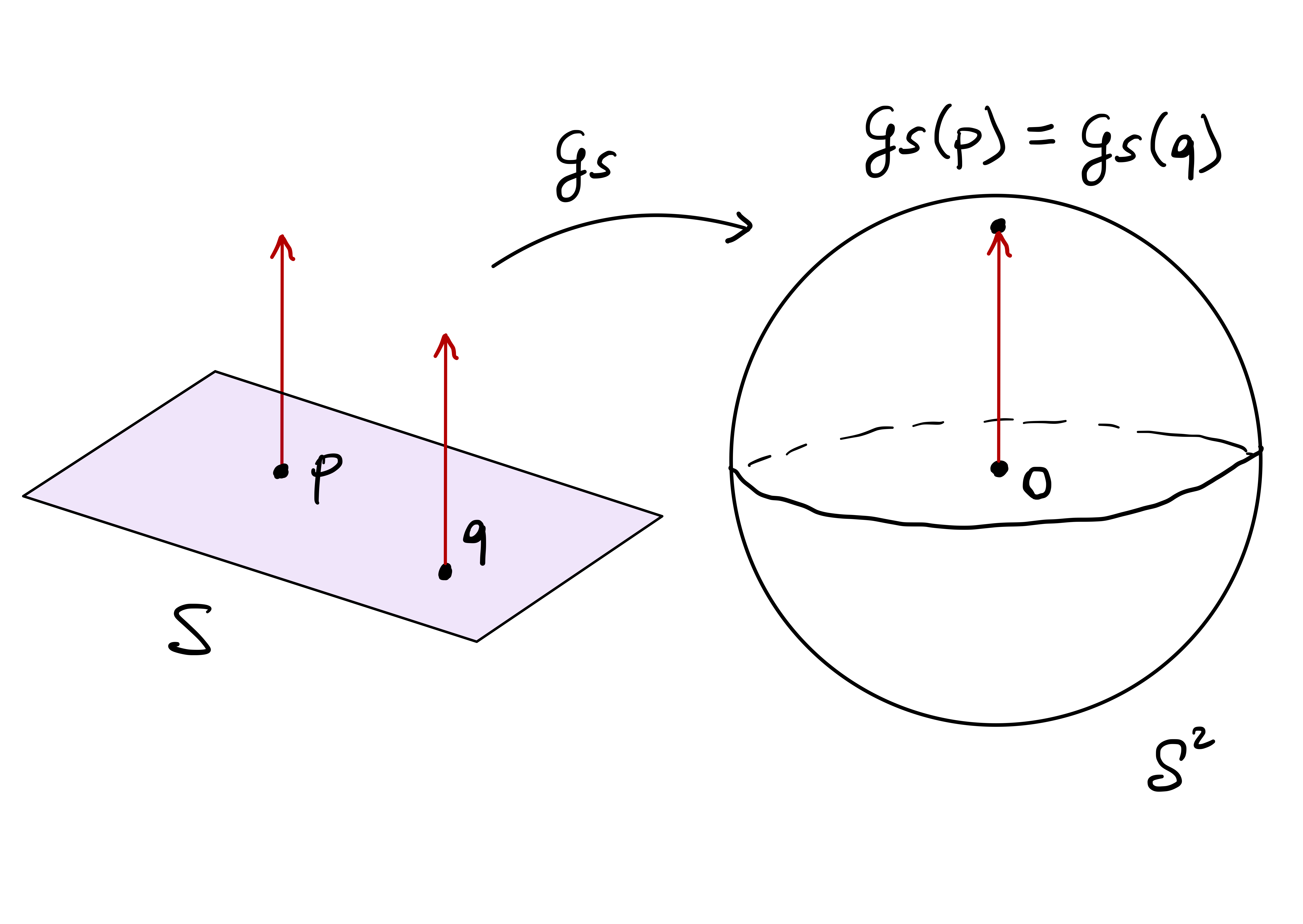
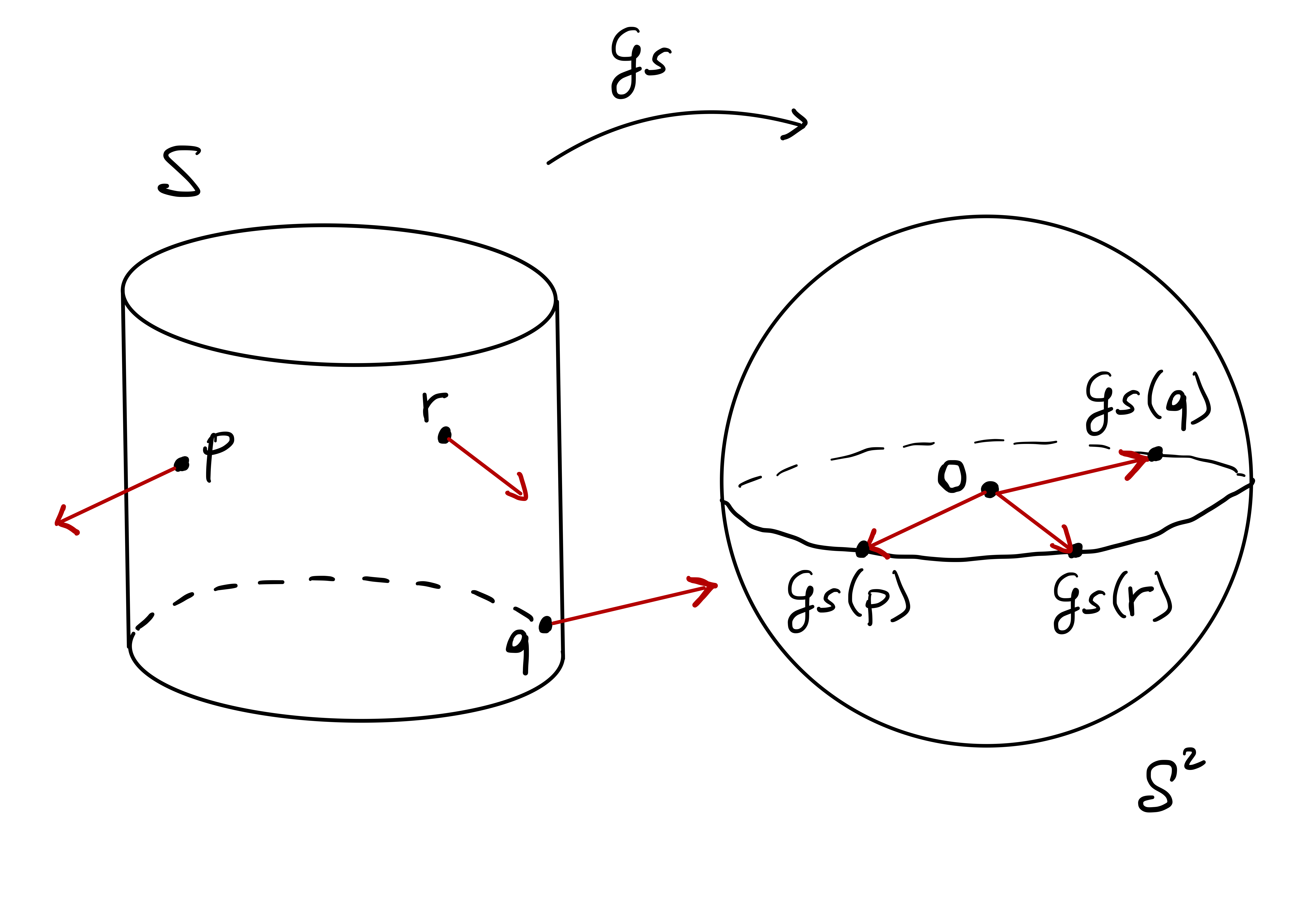
Remark 150
By definition, the Gauss map is a smooth function between surfaces. Therefore the differential of \(\mathcal{G}_{\mathcal{S}}\) is well defined, and \[ d_{\mathbf{p}} {\mathcal{G}}_{\mathcal{S}} \colon T_{\mathbf{p}} \mathcal{S}\to T_{{\mathcal{G}}_{\mathcal{S}}(\mathbf{p})} \mathbb{S}^2 \,, \] for all \(\mathbf{p}\in \mathcal{S}\). We have that \[ T_{{\mathcal{G}}_{\mathcal{S}}(\mathbf{p})} \mathbb{S}^2 = T_{\mathbf{p}} \mathcal{S}\,, \tag{4.11}\] see Figure 4.14. Therefore \[ d_{\mathbf{p}} {\mathcal{G}}_{\mathcal{S}} \colon T_{\mathbf{p}} \mathcal{S}\to T_{\mathbf{p}} \mathcal{S}\,. \]
Proof. The tangent plane \(T_{{\mathcal{G}}_{\mathcal{S}}(\mathbf{p})} \mathbb{S}^2\) passes through the origin and \[ \mathcal{G}(\mathbf{p}) \perp T_{{\mathcal{G}}_{\mathcal{S}}(\mathbf{p})} \mathbb{S}^2 \,. \] By definition \(\mathcal{G}(\mathbf{p}) = \mathbf{N}(\mathbf{p})\), and thus \[ \mathbf{N}(\mathbf{p}) \perp T_{{\mathcal{G}}_{\mathcal{S}}(\mathbf{p})} \mathbb{S}^2 \,. \] Since by definition \[ \mathbf{N}(\mathbf{p}) \perp T_{\mathbf{p}} \mathcal{S}\,, \] we infer (4.11).
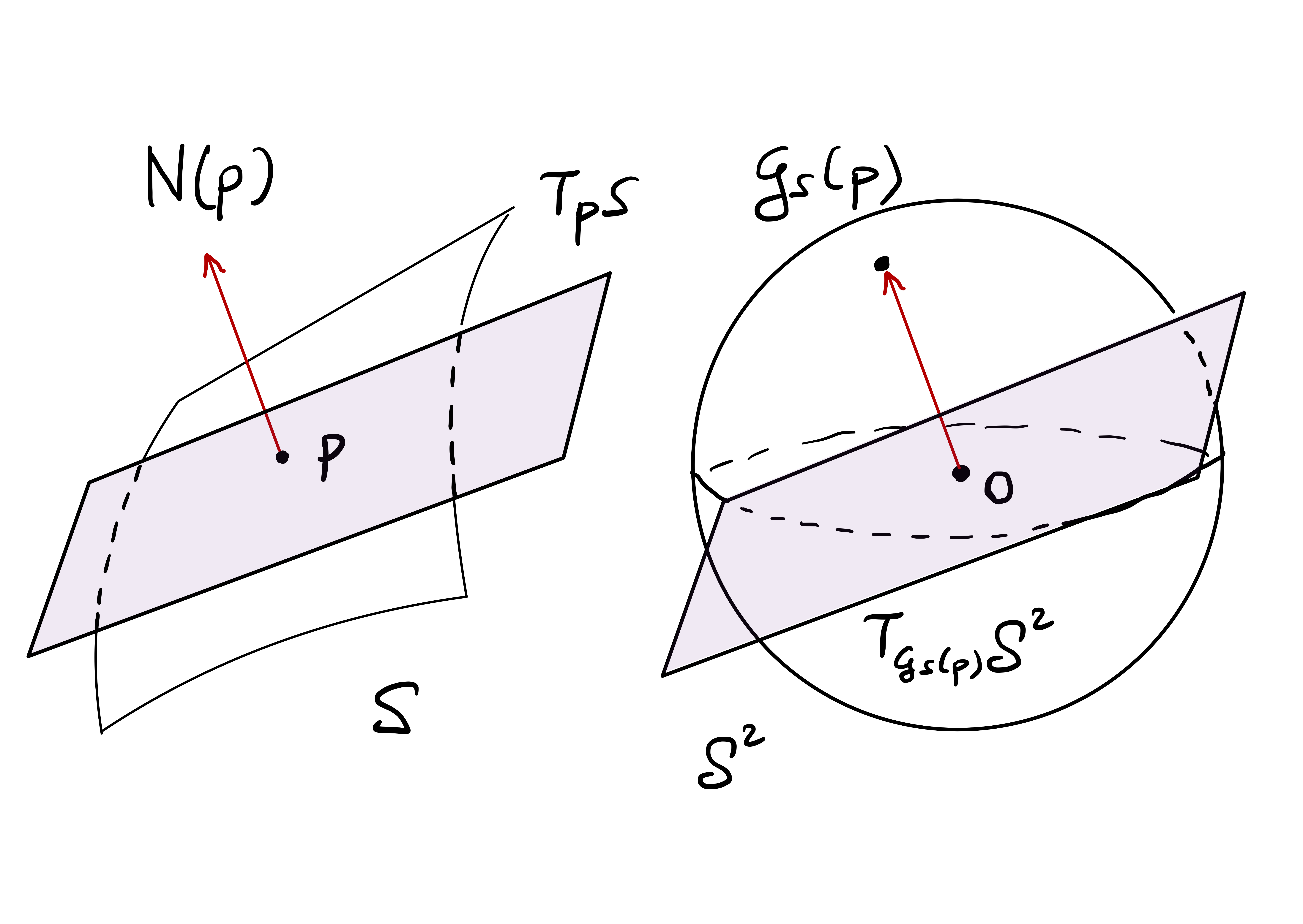
Definition 151: Weingarten map
Important
Remark 152
The Weingarten map allows us to define a bilnear form on \(T_{\mathbf{p}} \mathcal{S}\). We call such bilinear form the second fundamental form of \(\mathcal{S}\).
Definition 153: Second fundamental form of a surface
Remark 154
The second fudamental form \(II_{\mathbf{p}}\) of \(\mathcal{S}\) is bilinear.
Indeed, \(\mathcal{W}_{\mathbf{p},\mathcal{S}}\) is linear, being the differential of a smooth map. Hence \(II_{\mathbf{p}}\) is bilinear, given that the scalar product is bilinear.
Remark 155: Matrix of the second fundamental form
Theorem 156
Let \(\mathcal{S}\) be an orientable surface and \({\pmb{\sigma}}\colon U \to \mathbb{R}^3\) be a regular chart. Let \(\mathbf{p}\in {\pmb{\sigma}}(U)\).
The second funamental form \(II_{\mathbf{p}}\) is a symmetric bilinear map.
It holds \[ II_{\mathbf{p}} (\mathbf{v},\mathbf{w}) = (du (\mathbf{v}), dv(\mathbf{v}) ) \, \left( \begin{array}{cc} L & M \\ M & N \end{array} \right) \, (du(\mathbf{w}) , dv(\mathbf{w}))^T \,, \] for all \(\mathbf{v},\mathbf{w}\in T_{\mathbf{p}} \mathcal{S}\), where \[ L = {\pmb{\sigma}}_{uu} \cdot \mathbf{N}\,, \quad M = {\pmb{\sigma}}_{uv} \cdot \mathbf{N}\,, \quad N = {\pmb{\sigma}}_{vv} \cdot \mathbf{N}\,. \]
\(\mathscr{F}_2\) is the quadratic form associated to \(II_{\mathbf{p}}\), that is, \[ \mathscr{F}_2 (\mathbf{v}) = {II}_{\mathbf{p}} (\mathbf{v},\mathbf{v}) \,, \quad \forall \, \mathbf{v}\in T_{\mathbf{p}} \mathcal{S}\,. \]
To prove Theorem 156 we use the following two Lemmas.
Lemma 157
Proof
Lemma 158
Proof
We can now prove Theorem 156
Proof: Proof of Theorem 156
4.12.4 Matrix of Weingarten map
The Weingarten map is a linear map \[ \mathcal{W}_{\mathbf{p},\mathcal{S}} \colon T_{\mathbf{p}} \mathcal{S}\to T_{\mathbf{p}} \mathcal{S}\,. \] We would like to find a formula to compute \(\mathcal{W}_{\mathbf{p},\mathcal{S}}\). This is easily done: Given a chart \({\pmb{\sigma}}\) at \(\mathbf{p}\), we have that \(\{{\pmb{\sigma}}_u,{\pmb{\sigma}}_v\}\) is a basis for the vector space \(T_{\mathbf{p}} \mathcal{S}\). Therefore there exists a \(2 \times 2\) matrix \(A\) which represents \(\mathcal{W}_{\mathbf{p},\mathcal{S}}\), that is, \[ \mathcal{W}_{\mathbf{p},\mathcal{S}}(\mathbf{v}) = A \mathbf{v}\,, \quad \forall \, \mathbf{v}\in T_{\mathbf{p}} \mathcal{S}\,. \] It turns out that \[ A = \mathscr{F}_1^{-1} \mathscr{F}_2 \,, \] where we recall that \[ \mathscr{F}_1 = \left( \begin{array}{cc} E & F \\ F & G \end{array} \right)\,, \quad \mathscr{F}_2 = \left( \begin{array}{cc} L & M \\ M & N \end{array} \right) \,, \] where \[\begin{align*} E & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_u \,, & F & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v \, , & G & = {\pmb{\sigma}}_v \cdot {\pmb{\sigma}}_v \,, \\ L & = {\pmb{\sigma}}_{uu} \cdot \mathbf{N}\, , & M & = {\pmb{\sigma}}_{uv} \cdot \mathbf{N}\,, & N & = {\pmb{\sigma}}_{vv} \cdot \mathbf{N}\,, \end{align*}\] and \[ \mathbf{N}= \frac{ {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v }{ \left\| {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \right\| } \,. \] Let us prove this claim.
Theorem 159: Matrix of Weingarten map
Proof
Indeed, recall Cauchy-Schwarz inequality: \[ \mathbf{v}\cdot \mathbf{v}\leq \| \mathbf{v}\| \| \mathbf{w}\| \,, \quad \forall \, \mathbf{v}, \mathbf{w}\in \mathbb{R}^3 \,, \] where the inequality is strict if and only if \(\mathbf{v}\) and \(\mathbf{w}\) are linearly independent. Since \(\mathcal{S}\) is regular, we have that \({\pmb{\sigma}}_u\) and \({\pmb{\sigma}}_v\) are linearly independent. Therefore by Cauchy-Schwarz we have \[ {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v < \left\| {\pmb{\sigma}}_u \right\| \left\| {\pmb{\sigma}}_v \right\| \,, \] and so, squaring both sides, \[ \left( {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v \right)^2 < \left\| {\pmb{\sigma}}_u \right\|^2 \left\| {\pmb{\sigma}}_v \right\|^2 \,. \] Hence \[\begin{align*} \det (\mathscr{F}_1) & = EG-F^2 \\ & = \left({\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_u \right) \left({\pmb{\sigma}}_v \cdot {\pmb{\sigma}}_v \right) - \left({\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v \right)^2 \\ & = \left\| {\pmb{\sigma}}_u \right\|^2 \left\| {\pmb{\sigma}}_v \right\|^2 - \left({\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v \right)^2 > 0 \,. \end{align*}\]
In particular the matrix \(\mathscr{F}_1\) is invertible and thus \[ A = \mathscr{F}_1^{-1} \mathscr{F}_2 \,, \] concluding the proof.
Important
Notation
Example 160: Helicoid
The Helicoid is charted by \[ {\pmb{\sigma}}(u,v) = (u \cos (v), u \sin(v) , \lambda v) \,, \quad u \in [0,1] \,, \, v \in [0,4\pi) \,, \] where \(\lambda>0\) is a constant, see Figure 4.15. Prove that the matrix of the Weingarten map is \[ \mathcal{W}= \left( \begin{array}{cc} 0 & - \dfrac{\lambda}{(u^2 + \lambda^2)^{1/2}} \\ \dfrac{\lambda}{(u^2 + \lambda^2)^{3/2}} & 0 \end{array} \right) \,. \]
Solution. We compute \[\begin{align*} {\pmb{\sigma}}_u & = ( \cos(v), \sin(v), 0 ) \\ {\pmb{\sigma}}_v & = ( - u \sin(v), u \cos(v), \lambda ) \\ {\pmb{\sigma}}_{uu} & = ( 0, 0, 0 ) \\ {\pmb{\sigma}}_{uv} & = (- \sin(v), \cos(v), 0 ) \\ {\pmb{\sigma}}_{vv} & = ( - u \cos(v), - u \sin(v), 0 ) \\ \end{align*}\] from which \[\begin{align*} E & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_u = 1 \\ F & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v = 0 \\ G & = {\pmb{\sigma}}_v \cdot {\pmb{\sigma}}_v = u^2 + \lambda^2 \,, \end{align*}\] so that the first fundamental form is \[ \mathscr{F}_1 = \left( \begin{array}{cc} E & F \\ F & G \end{array} \right) = \left( \begin{array}{cc} 1 & 0 \\ 0 & u^2 + \lambda^2 \end{array} \right) \,. \] Since \(\mathscr{F}_1\) is diagonal, the inverse is immediately computed \[ \mathscr{F}_1^{-1} = \left( \begin{array}{cc} 1 & 0 \\ 0 & \dfrac{1}{u^2 + \lambda^2} \end{array} \right) \,. \] Moreover \[\begin{align*} {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v & = \left| \begin{array}{ccc} \mathbf{i}& \mathbf{j}& \mathbf{k}\\ \cos(v) & \sin(v) & 0 \\ -u \sin(v) & u \cos(v) & \lambda \end{array} \right| \\ & = (\lambda \sin (v), - \lambda \cos(v), u) \end{align*}\] and so \[ \left\| {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \right\| = \sqrt{u^2 + \lambda^2} \,. \] The standard unit normal to \({\pmb{\sigma}}\) is \[ \mathbf{N}= \frac{ {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v }{ \left\| {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \right\| } = \frac{1}{\sqrt{u^2 + \lambda^2}} \, (\lambda \sin(v), -\lambda \cos(v), u) \,. \] Hence \[\begin{align*} L & = {\pmb{\sigma}}_{uu} \cdot \mathbf{N}= 0 \\ M & = {\pmb{\sigma}}_{uv} \cdot \mathbf{N}= - \frac{\lambda}{\sqrt{u^2 + \lambda^2}} \\ N & = {\pmb{\sigma}}_{vv} \cdot \mathbf{N}= 0 \\ \end{align*}\] and the second funamental form \(\mathscr{F}_2\) is \[ \mathscr{F}_2 = \left( \begin{array}{cc} L & M \\ M & N \end{array} \right) = \left( \begin{array}{cc} 0 & - \dfrac{\lambda}{\sqrt{u^2 + \lambda^2}} \\ - \dfrac{\lambda}{\sqrt{u^2 + \lambda^2}} & 0 \end{array} \right) \,. \] Finally \[\begin{align*} \mathcal{W}& = \mathscr{F}_1^{-1} \mathscr{F}_2 \\ & = \left( \begin{array}{cc} 1 & 0 \\ 0 & \dfrac{1}{u^2 + \lambda^2} \end{array} \right) \left( \begin{array}{cc} 0 & - \dfrac{\lambda}{\sqrt{u^2 + \lambda^2}} \\ - \dfrac{\lambda}{\sqrt{u^2 + \lambda^2}} & 0 \end{array} \right) \\ & = \left( \begin{array}{cc} 0 & - \dfrac{\lambda}{(u^2 + \lambda^2)^{1/2}} \\ \dfrac{\lambda}{(u^2 + \lambda^2)^{3/2}} & 0 \end{array} \right) \,. \end{align*}\]
Example 161
Find the Weingarten matrix of the following surface chart \[ {\pmb{\sigma}}(u, v) = \left(u-v, u+v, u^{2}+v^{2}\right) \,. \]
Solution. Start by computing the first fundamental form: \[\begin{align*} {\pmb{\sigma}}_{u} & =(1,1,2u) \\ {\pmb{\sigma}}_{v} & =(-1,1,2v) \\ E & = {\pmb{\sigma}}_{u} \cdot {\pmb{\sigma}}_u = 2 (1+2u^2) \\ F & = {\pmb{\sigma}}_{u} \cdot {\pmb{\sigma}}_v = 4uv \\ G & = {\pmb{\sigma}}_{v} \cdot {\pmb{\sigma}}_v = 2 (1+2v^2) \end{align*}\] so that \[ \mathscr{F}_{1}= \left( \begin{array}{ll} E & F \\ F & G \end{array} \right) = \left(\begin{array}{ll} 2(1 + 2u^2) & 4uv \\ 4uv & 2(1 + 2v^2) \end{array}\right) \] The determinant of \(\mathscr{F}_1\) is \[ \det (\mathscr{F}_1) = 4 (1+2u^2 + 2v^2) \] and therefore \[\begin{align*} \mathscr{F}_{1}^{-1} & = \frac{1}{\det (\mathscr{F}_1)} \left( \begin{array}{ll} G & -F \\ -F & E \end{array} \right) \\ & = \frac{1}{2(1 + 2u^2 + 2v^2)} \,\left(\begin{array}{ll} 1 + 2v^2 & -2uv \\ - 2uv & 1 + 2u^2 \end{array}\right) \,. \end{align*}\] We now need to compute the second fundamental form \[\begin{align*} {\pmb{\sigma}}_{u u} & =(0,0,2) \\ {\pmb{\sigma}}_{u v} & =(0,0,0) \\ {\pmb{\sigma}}_{v v} & =(0,0,2) \\ {\pmb{\sigma}}_{u} \times {\pmb{\sigma}}_{v} & =\left|\begin{array}{ccc} \mathbf{i}& \mathbf{j}& \mathbf{k}\\ 1 & 1 & 2 u \\ -1 & 1 & 2 v \end{array}\right| \\ & =2(v-u,-u-v, 1) \\ \left\|{\pmb{\sigma}}_{u} \times {\pmb{\sigma}}_{v}\right\| & =2\left( 1 + 2u^2 + 2v^2\right)^{\frac{1}{2}} \\ \mathbf{N}& =\frac{(v-u,-u-v, 1)}{ \left( 1 + 2 u^2 + 2 v^2 \right)^{\frac{1}{2}}} \\ L & = {\pmb{\sigma}}_{uu} \cdot \mathbf{N}=\frac{2}{\left( 1 + 2u^{2}+ 2v^{2}\right)^{\frac{1}{2}}} \\ M & = {\pmb{\sigma}}_{uv} \cdot \mathbf{N}= 0 \\ N & = {\pmb{\sigma}}_{vv} \cdot \mathbf{N}= \frac{2}{\left(1 + 2u^{2}+ 2v^{2}\right)^{\frac{1}{2}}} \end{align*}\] so that \[\begin{align*} \mathscr{F}_{2} & = \left(\begin{array}{ll} L & M \\ M & N \end{array}\right) \\ & = \frac{2}{\left( 1 + 2u^{2}+ 2v^{2}\right)^{\frac{1}{2}}} \, \left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right) \,. \end{align*}\] The matrix of the Weingarten map is \[\begin{align*} \mathcal{W}& = \mathscr{F}_1^{-1} \mathscr{F}_2 \\ & = \frac{1}{(1 + 2u^2 + 2v^2)^{\frac32}} \,\left(\begin{array}{ll} 1 + 2v^2 & -2uv \\ - 2uv & 1 + 2u^2 \end{array}\right) \,. \end{align*}\]
4.13 Curvatures
Curvatures of a surface \(\mathcal{S}\) are scalars associated to the Weingarten map \(\mathcal{W}_{\mathbf{p},\mathcal{S}}\). We will define:
- Gaussian curvature
- Mean curvature
- Principal curvatures
- Normal curvature
- Geodesic curvature
4.13.1 Gaussian and mean curvature
The Weingarten map of \(\mathcal{S}\) encodes the rate of change of the standard unit normal \(\mathbf{N}\). We use this map to produce scalar values, which we call curvatures. The first two curvatures that we consider are called Gaussian and mean curvatures.
Definition 162: Gaussian and mean curvature
Let \(\mathcal{S}\) be an orientable surface and let \(\mathcal{W}\) denote the matrix of the Weingarten map \(\mathcal{W}_{\mathbf{p},\mathcal{S}}\) of \(\mathcal{S}\) at \(\mathbf{p}\). We define:
The Gaussian curvature of \(\mathcal{S}\) at \(\mathbf{p}\) as \[ K := \det (\mathcal{W}) \,, \]
The mean curvature of \(\mathcal{S}\) at \(\mathbf{p}\) as \[ H := \frac12 \, \operatorname{trace} (\mathcal{W}) \,, \]
Notation: Trace of a \(2 \times 2\) matrix
Remark 163
The Gaussian curvature and mean curvature do not depend on the choice of basis of \(T_{\mathbf{p}} \mathcal{S}\). Indeed, if \(\widetilde{\mathcal{W}}\) is the matrix of the Weingarten map with respect to the basis \(\{\widetilde{{\pmb{\sigma}}}_u,\widetilde{{\pmb{\sigma}}}_v\}\) of \(T_{\mathbf{p}} \mathcal{S}\), then \[ \det (\mathcal{W}) = \det (\widetilde{\mathcal{W}}) \,, \quad \operatorname{trace} (\mathcal{W}) = \operatorname{trace} (\widetilde{\mathcal{W}}) \,. \]
The above is true by a general linear algebra result: The determinant and trace of a matrix are invariant under change of basis.
Since we have shown that the matrix of the Weingarten map is \[ \mathcal{W}= \mathscr{F}_1^{-1} \mathscr{F}_2 \,, \] we can express \(K\) and \(H\) in terms of the first and second fundamental forms.
Proposition 164
Proof
Example 165: Plane
Example 166: Unit cylinder
4.13.2 Principal curvatures
Let \(V\) be a two-dimensional vector space. For a linear map \(L \colon V \to V\) we say that \(\lambda \in \mathbb{R}\) is an eigenvalue of \(L\) with eigenvector \(\mathbf{v}\in V\) if \[ L(\mathbf{v}) = \lambda \mathbf{v}\,, \quad \mathbf{v}\neq 0 \,. \] Suppose \(A \in \mathbb{R}^{2 \times 2}\) is the matrix of \(L\) with respect to a basis \(\{\mathbf{v}_1,\mathbf{v}_2\}\) of \(V\). Denote by \[ \mathbf{x}= (\lambda,\mu) \,, \quad \mathbf{v}= \lambda \mathbf{w}_1 + \mu \mathbf{w}_2 \,. \] the vector of coordinates of \(\mathbf{v}\). Then \[ A\mathbf{v}= \lambda \mathbf{v}\,, \] meaning that \(\lambda\) is an eigenvalue of \(A\) with eigenvector \(\mathbf{x}\). The eigenvalues of \(A\) can be computed by solving the characteristic equation \[ P(\lambda) = 0 \,, \quad P(\lambda) := \det \left( A - \lambda I \right) \,, \] where \(P\) is the characteristic polynomial of \(A\). Finally, we recall that \(A \in \mathbb{R}^{2 \times 2}\) is diagonalizable if there exists a diagonal matrix \(D\) and an invertible matrix \(P\) such that \[ A = P^{-1} D P \,. \]
Theorem 167
Proof
The matrix version of Theorem 167 is given in the following Corollary.
Corollary 168
Let \(\mathcal{S}\) be orientable, and let \(\mathcal{W}\) the matrix of the Weingarten map \(\mathcal{W}_{\mathbf{p},\mathcal{S}}\) with respect to the basis \(\{{\pmb{\sigma}}_u,{\pmb{\sigma}}_v\}\) of \(T_{\mathbf{p}}\mathcal{S}\), where \({\pmb{\sigma}}\) is a regular chart at \(\mathbf{p}\). Let \(\kappa_1,\kappa_2,\mathbf{t}_1,\mathbf{t}_2\) be as in Theorem 167. Let \(\lambda_1, \lambda_2, \mu_1, \mu_2 \in \mathbb{R}\) be such that \[ \mathbf{t}_1 = \lambda_1 {\pmb{\sigma}}_u + \mu_1 {\pmb{\sigma}}_v \,, \quad \mathbf{t}_2 = \lambda_2 {\pmb{\sigma}}_u + \mu_2 {\pmb{\sigma}}_v \,. \] and denote \[ \mathbf{x}_1 = (\lambda_1,\mu_1) \,, \quad \mathbf{x}_2 = (\lambda_2,\mu_2) \,. \] They hold:
The scalars \(\kappa_1,\kappa_2\) are eingenvalues of \(\mathcal{W}\) of eigenvectors \(\mathbf{x}_1\) and \(\mathbf{x}_2\), that is, \[ \mathcal{W}\mathbf{x}_1 = \kappa_1 \mathbf{x}_1 \,, \quad \mathcal{W}\mathbf{x}_2 = \kappa_2 \mathbf{x}_2 \,. \]
The matrix \(\mathcal{W}\) is diagonalizable, with \[ \mathcal{W}= P^{-1} D P \,, \quad D = \left( \begin{array}{cc} \kappa_1 & 0 \\ 0 & \kappa_2 \end{array} \right) \,, \quad P = \left( \begin{array}{cc} \lambda_1 & \lambda_2 \\ \mu_1 & \mu_2 \end{array} \right) \,. \]
Proof
The eigenvalues and eigenvectors of the weingarten map have a name.
Definition 169: Principal curvatures and vectors
Let \(\mathcal{S}\) be an orientable surface and \(\mathcal{W}_{\mathbf{p},\mathcal{S}}\) be the Weingarten map of \(\mathcal{S}\) at \(\mathbf{p}\). We define:
The principal curvatures of \(\mathcal{S}\) at \(\mathbf{p}\) are the eigenvalues \(\kappa_1, \kappa_2\) of \(\mathcal{W}_{\mathbf{p},\mathcal{S}}\).
The principal vectors corresponding to \(\kappa_1\) and \(\kappa_2\) are the eigenvectors \(\mathbf{t_1}, \mathbf{t}_2\).
Remark 170: Computing principal curvatures and vectors
Corollary 168 gives an explicit way to compute the principal curvatures and vectors:
Compute the eigenvalues of \(\mathcal{W}\). This is done by solving for \(\kappa\) the equation \[ \det(\mathcal{W}- \kappa I) = 0 \,. \] This gives one of the principal curvatures \[ \kappa_i = \kappa \]
Compute the eigenvector(s) related to the eigenvalue \(\kappa\). This is done by finding scalars \(\lambda\), \(\mu\) which solve the linear system \[ (\mathcal{W}- \kappa_i I) \left( \begin{array}{c} \lambda \\ \mu \end{array} \right) = 0 \] This gives the eigenvector of \(\mathcal{W}\) \[ \mathbf{x}_i = (\lambda,\mu) \]
The principal vector associated to \(\kappa_i\) is
\[ \mathbf{t}_i = \lambda {\pmb{\sigma}}_u + \mu {\pmb{\sigma}}_v \]
Remark 171: Computing principal curvatures and vectors
The principal curvatures are related to the Gaussian and mean curvatures.
Proposition 172
Proof
Important
Example 173: Unit Cylinder
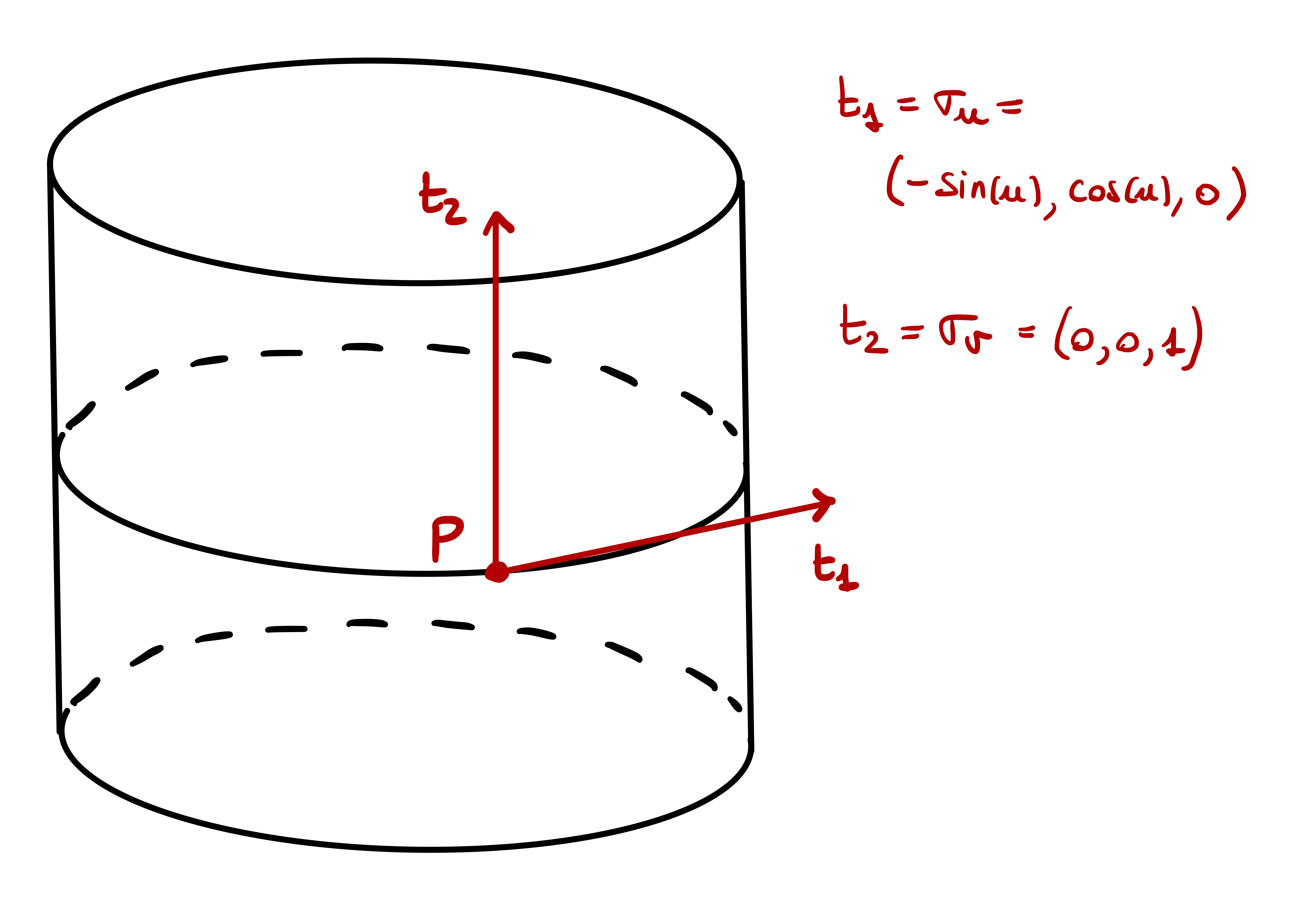
Example 174: Sphere
Consider the chart for the sphere \[ {\pmb{\sigma}}(u, v)=(\cos (u) \sin (v), \sin (u) \sin (v), \cos (v)) \] Prove that \[ \mathcal{F}_1 = \mathcal{F}_2 = \left( \begin{array}{cc} \sin^2(v) & 0 \\ 0 & 1 \end{array} \right) \,, \quad \mathcal{W}= \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \,, \] and \[ K = H = \kappa_1 = \kappa_2 =1 \,, \quad \mathbf{t}_1 = {\pmb{\sigma}}_u \,, \quad \mathbf{t}_2 = {\pmb{\sigma}}_v \,. \]
Solution. We compute \[\begin{align*} {\pmb{\sigma}}_u & = (-\sin(u)\sin(v), \cos(u)\sin(v),0) \\ {\pmb{\sigma}}_v & = (\cos(u)\cos(v), \sin(u)\cos(v), - \sin(v)) \\ E & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_u = \sin^2(v) \\ F & = {\pmb{\sigma}}_u \cdot {\pmb{\sigma}}_v = 0\\ G & = {\pmb{\sigma}}_v \cdot {\pmb{\sigma}}_v = 1 \end{align*}\] and therefore the first fundamental form is \[ \mathcal{F}_1 = \left( \begin{array}{cc} \sin^2(v) & 0 \\ 0 & 1 \end{array} \right) \,. \] Moreover \[\begin{align*} {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v & = \left| \begin{array}{ccc} \mathbf{i}& \mathbf{j}& \mathbf{k}\\ -\sin(u)\sin(v) & \cos(u)\sin(v) & 0 \\ \cos(u)\cos(v) & \sin(u)\cos(v) & - \sin(v) \end{array} \right| \\ & = (-\cos(u)\sin^2(v), -\sin(u) \sin^2(v), - \cos(v)\sin(v)) \\ \| {\pmb{\sigma}}_u \times {\pmb{\sigma}}_v \| & = |\sin(v)| \\ \mathbf{N}& = (- \cos(u) \sin(v), -\sin(u)\sin(v), -\cos(v) ) \\ {\pmb{\sigma}}_{uu} & = (-\cos(u)\sin(v), -\sin(u)\sin(v), 0 ) \\ {\pmb{\sigma}}_{uv} & = (-\sin(u)\cos(v), \cos(u)\cos(v), 0 ) \\ {\pmb{\sigma}}_{vv} & = (-\cos(u)\sin(v), -\sin(u)\sin(v), -\cos(v) ) \\ L & = {\pmb{\sigma}}_{uu} \cdot \mathbf{N}= \sin^{2}(v) \\ M & ={\pmb{\sigma}}_{uv} \cdot \mathbf{N}= 0 \\ N & = {\pmb{\sigma}}_{vv} \cdot \mathbf{N}= 1 \end{align*}\] so that the second fundamental form is \[ \mathcal{F}_2 = \left( \begin{array}{cc} \sin^2(v) & 0 \\ 0 & 1 \end{array} \right) \,. \] In particular the matrix of the Weingarten map is \[ \mathcal{W}= \mathcal{F}_1^{-1}\mathcal{F}_2 = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \] Since \(\mathcal{W}\) is diagonal, the principal curvatures are \[ \kappa_1 = \kappa_2 = 1 \] and the principal vectors \[ \mathbf{t}_1 = {\pmb{\sigma}}_u \,, \quad \mathbf{t}_2 = {\pmb{\sigma}}_v \,. \] Finally, we have that \[ H = \frac{\kappa_1 + \kappa_2}{2} = 1 \,, \quad K= \kappa_1 \kappa_2 = 1 \,. \]
Example 175: Torus
4.13.3 Normal and geodesic curvatures
Let \(\mathcal{S}\) be a regular surface and consider all the curves \({\pmb{\gamma}}\) on \(\mathcal{S}\) passing through the point \(\mathbf{p}\in \mathcal{S}\).
Question 176
We start our analysis with the following proposition.
Proposition 177
Proof
Important
Proposition 178
Proof
Part 2. Taking the scalar product of (4.12) with \(\mathbf{N}\) yields \[ \ddot{{\pmb{\gamma}}}\cdot \mathbf{N}= \kappa_n \left\| \mathbf{N} \right\|^2 + \kappa_g \left( \mathbf{N}\times \dot{{\pmb{\gamma}}}\right) \cdot \mathbf{N}= \kappa_n \,, \] where we used that \(\mathbf{N}\) and \(\mathbf{N}\times \dot{{\pmb{\gamma}}}\) are orthonormal vectors. Similarly, taking the scalar product of (4.12) with \(\mathbf{N}\times \dot{{\pmb{\gamma}}}\) yields the second equation in (4.13).
Part 3. By (4.12) we infer \[\begin{align*} \left\| \ddot{{\pmb{\gamma}}} \right\|^2 & = \kappa_n^2 \left\| \mathbf{N} \right\|^2 + 2 \kappa_n \kappa_g \mathbf{N}\cdot \left(\mathbf{N}\times \dot{{\pmb{\gamma}}}\right) + \kappa_g^2 \left\| \mathbf{N}\times \dot{{\pmb{\gamma}}} \right\|^2 \\ & = \kappa_n^2 + \kappa_g^2 \,, \end{align*}\] where we used that \(\mathbf{N}\) and \(\mathbf{N}\times \dot{{\pmb{\gamma}}}\) are orthonormal. Since \(\kappa(t) = \left\| \ddot{{\pmb{\gamma}}}(t) \right\|\), we get (4.14).
Part 4. Recalling that \[ \ddot{{\pmb{\gamma}}}= \kappa \mathbf{n}\,, \] from the first equation in (4.13) we obtain \[\begin{align*} \kappa_n & = \ddot{{\pmb{\gamma}}}\cdot \mathbf{N}\\ & = \kappa \mathbf{n}\cdot \mathbf{N}\\ & = \kappa \| \mathbf{n}\|^2 \| \mathbf{N}\|^2 \cos(\phi) \\ & = \kappa \cos(\phi) \,, \end{align*}\] where we used that \(\mathbf{n}\) and \(\mathbf{N}\) have unit norm. Hence the first equation in (4.15) is established. By (4.14) we get \[\begin{align*} \kappa_g^2 & = \kappa^2 - \kappa_n^2 \\ & = \kappa^2 \cos^2(\phi) - \kappa_n^2 \\ & = \kappa^2 (\cos^2(\phi) - 1 ) \\ & = \kappa^2 \sin^2(\phi) \,, \end{align*}\] from which we obtain the second equation in (4.15).
The quantities \(\kappa_n\) and \(\kappa_g\) are the normal and geodesic curvatures of \({\pmb{\gamma}}\).
Definition 179: Normal and geodesic curvature
Let \(\mathcal{S}\) be regular and \({\pmb{\gamma}}\colon (a,b) \to \mathcal{S}\) a unit speed curve. By (4.12) we have \[ \ddot{{\pmb{\gamma}}}= \kappa_{n} \mathbf{N}+ \kappa_{g} (\mathbf{N}\times \dot{{\pmb{\gamma}}}) \] for \(\mathbf{N}\) the standard unit normal to \(\mathcal{S}\) and scalars \(\kappa_n , \kappa_g \in \mathbb{R}\). We call
- \(\kappa_{n}\) the normal curvature of \({\pmb{\gamma}}\),
- \(\kappa_{g}\) the geodesic curvature of \({\pmb{\gamma}}\).
The normal curvature \(\kappa_n\) can be computed via the second fundamental form, as shown in the theorem below.
Theorem 180
Let \(\mathcal{S}\) be a regular surface and \({\pmb{\gamma}}\colon (a,b) \to \mathcal{S}\) a unit speed curve. Denote \(\mathbf{p}:= {\pmb{\gamma}}(t)\). We have:
The normal curvature \(\kappa_n\) satisfies \[ \kappa_n = {II}_{\mathbf{p}} (\dot{{\pmb{\gamma}}}, \dot{{\pmb{\gamma}}}) \,. \]
Let \({\pmb{\sigma}}\) be a chart for \(\mathcal{S}\) at \(\mathbf{p}\). Then \[ {\pmb{\gamma}}(t)={\pmb{\sigma}}(u(t), v(t)) \] for some smooth functions \(u,v \colon (a,b) \to \mathbb{R}\), and \[ \kappa_{n}=L \dot{u}^{2}+2 M \dot{u} \dot{v}+N \dot{v}^{2} \,. \]
Proof
Part 2. Let \({\pmb{\sigma}}\) be a chart at \(\mathbf{p}\) and \[ {\pmb{\gamma}}(t) = {\pmb{\sigma}}(u(t),v(t)) \,. \] Differentiating the above expression we get \[ \dot{{\pmb{\gamma}}}(t) = \dot{u} {\pmb{\sigma}}_u + \dot{v} {\pmb{\sigma}}_v \,. \] By definition of \(du\) and \(dv\), see Definition 101, we have \[ du(\dot{{\pmb{\gamma}}}(t)) = \dot{u}(t) \,, \quad dv(\dot{{\pmb{\gamma}}}(t)) = \dot{v}(t) \,. \] Therefore, using Part 1 and Theorem 156, we obtain \[\begin{align*} \kappa_n & = II_{\mathbf{p}} (\dot{{\pmb{\gamma}}}(t) , \dot{{\pmb{\gamma}}}(t) ) \\ & = L du(\dot{{\pmb{\gamma}}}(t))^2 + 2M du(\dot{{\pmb{\gamma}}}(t)) dv(\dot{{\pmb{\gamma}}}(t)) + N dv(\dot{{\pmb{\gamma}}}(t))^2 \\ & = L \dot{u}^{2}+2 M \dot{u} \dot{v}+N \dot{v}^{2} \,. \end{align*}\]
Example 181: Curves on the sphere
Consider the chart for the sphere \[ {\pmb{\sigma}}(u, v)=(\cos (u) \sin (v), \sin (u) \sin (v), \cos (v)) \] Show that \[ \kappa_{n}(t)=1 \] for all unit speed curves on the sphere.
Solution. We have computed in Example 174 that the second fundamental form of \({\pmb{\sigma}}\) is \[ \mathcal{F}_2 = \sin^{2}(v) du^2 + dv^2 \] Let \({\pmb{\gamma}}\) be a unit speed curve on the sphere, that is, \[ {\pmb{\gamma}}(t)=\sigma(u(t), v(t)) \,. \tag{4.20}\] By Theorem 180 the normal curvature of \({\pmb{\gamma}}\) is \[ \kappa_{n}=\sin^{2}(v) \dot{u}^{2}+\dot{v}^{2} \,. \] Differentiating (4.20) we get \[\begin{align*} \dot{{\pmb{\gamma}}}(t) & = \frac{d}{dt} ( \cos(u(t)) \sin(v(t)), \sin(u(t)) \sin(v(t)), \cos(v(t)) ) \\ & = (-\dot{u} \sin (u) \sin (v)+\dot{v} \cos (u) \cos (v), \dot{u} \cos (u) \sin (v)+ \\ & \qquad \dot{v} \sin (u) \cos (v),-\dot{v} \sin (v)) \end{align*}\] so that \[ \| \dot{{\pmb{\gamma}}}(t) \|^2 = \sin^{2}(v) \dot{u}^{2}+\dot{v}^{2} \,. \] Since \({\pmb{\gamma}}\) is unit speed, we also get \[ \|\dot{{\pmb{\gamma}}}\|^{2} = 1 \,, \] showing that \[ \kappa_{n}=\sin^{2}(v) \dot{u}^{2}+\dot{v}^{2} = 1 \,, \] as required.
The normal curvature \(\kappa_n\) is related to the principal curvatures \(\kappa_1\) and \(\kappa_2\).
Theorem 182: Euler’s Theorem
Proof
As an immediate corollary of the Euler’s Theorem we get the next statement.
Corollary 183
Let \(\mathcal{S}\) be a regular surface and \(\kappa_1, \kappa_2\) its principal curvatures at \(\mathbf{p}\) with principal vectors \(\mathbf{t}_1,\mathbf{t}_2\). Then:
\(\kappa_{1}\) and \(\kappa_{2}\) are the minimum and maximum values of \(\kappa_{n}\), for all unit speed curves on \(\mathcal{S}\) passing through \(\mathbf{p}\).
The directions of lowest and highest curvature on \(\mathcal{S}\) are given by \(\mathbf{t}_1\) and \(\mathbf{t}_2\).
In Example 181 we have shown with a direct argument that \[ \kappa_n = 1 \] for all unit speed curves on the sphere. Thanks to Euler’s Theorem we can obtain an immediate proof of this fact.
Example 184: Curves on the sphere
4.13.4 Local shape of a surface
The principal curvatures \(\kappa_1\) and \(\kappa_2\) determine the maximum and minimum curvature of a surface \(\mathcal{S}\), see Corollary 183. Hence we can study the local shape of \(\mathcal{S}\) in function of \(\kappa_1\) and \(\kappa_2\).
Theorem 185: Local structure of surfaces
Proof
Thanks to Theorem 185 we can distinguish between \(4\) approximating shapes.
Definition 186: Local shape types
Let \(\mathcal{S}\) be a regular surface and denote by \(\kappa_1(\mathbf{p})\) and \(\kappa_2(\mathbf{p})\) its principal curvatures at \(\mathbf{p}\). The point \(\mathbf{p}\) is
Elliptic if \[ \kappa_1(\mathbf{p}) > 0 \,, \, \kappa_2(\mathbf{p}) > 0 \quad \mbox{ or } \quad \kappa_1(\mathbf{p}) < 0 \,, \, \kappa_2(\mathbf{p}) < 0 \] Then (4.22) is the equation of an elliptic paraboloid.
Hyperbolic if \[ \kappa_{1}(\mathbf{p})<0<\kappa_{2}(\mathbf{p}) \quad \mbox{ or } \quad \kappa_{2}(\mathbf{p})<0< \kappa_{1}(\mathbf{p}) \] Then (4.22) is the equation of a hyperbolic paraboloid.
Parabolic if \[ \kappa_{1}(\mathbf{p})=0 \, , \, \kappa_{2}(\mathbf{p}) \neq 0 \quad \mbox{ or } \quad \kappa_{2}(\mathbf{p}) \neq 0, \, \kappa_{1}(\mathbf{p})=0 \] Then (4.22) is the equation of a parabolic cylinder.
Planar if \[ \kappa_{1}(\mathbf{p})=\kappa_{2}(\mathbf{p}) = 0 \] Then (4.22) is the equation of a plane.
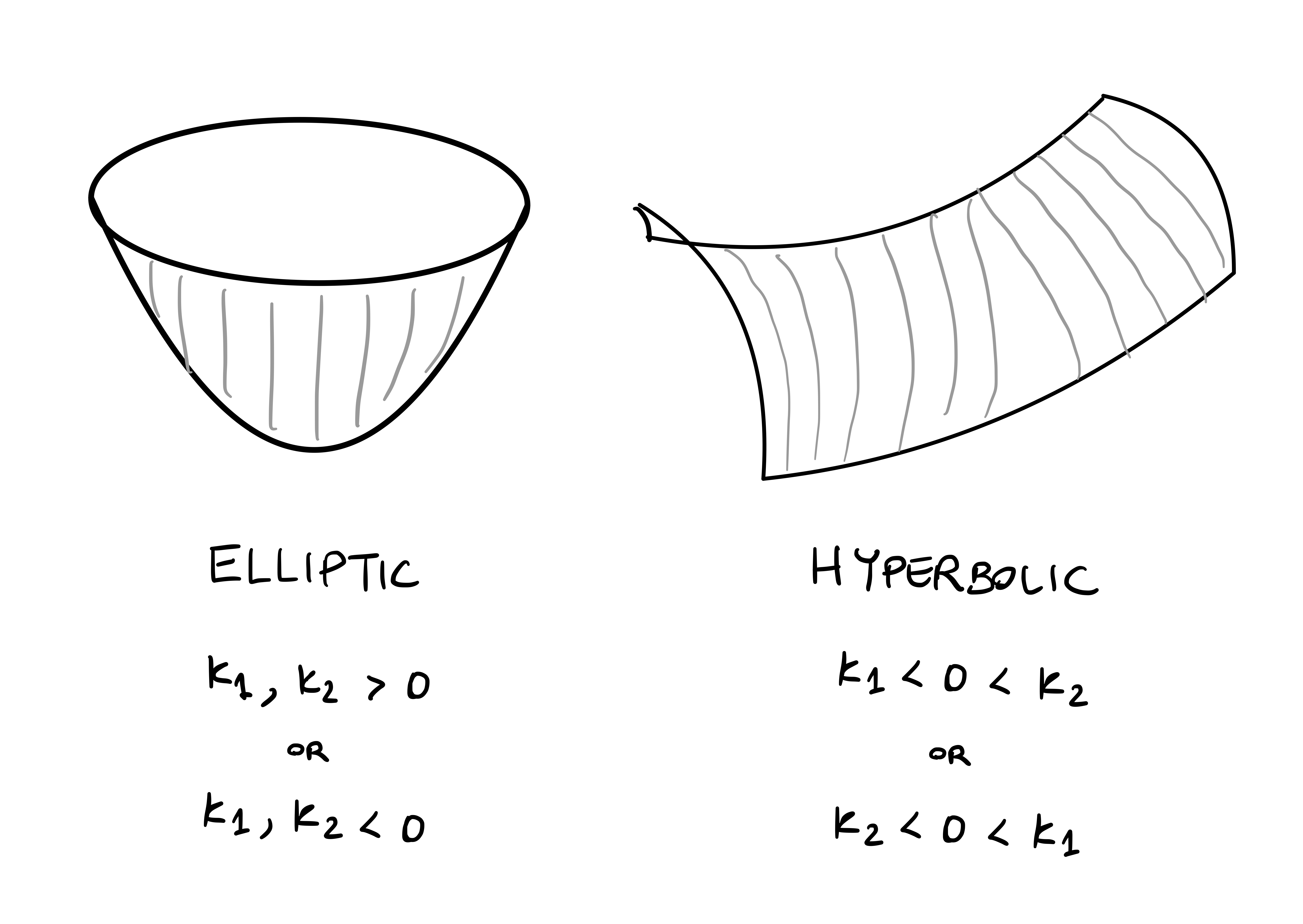
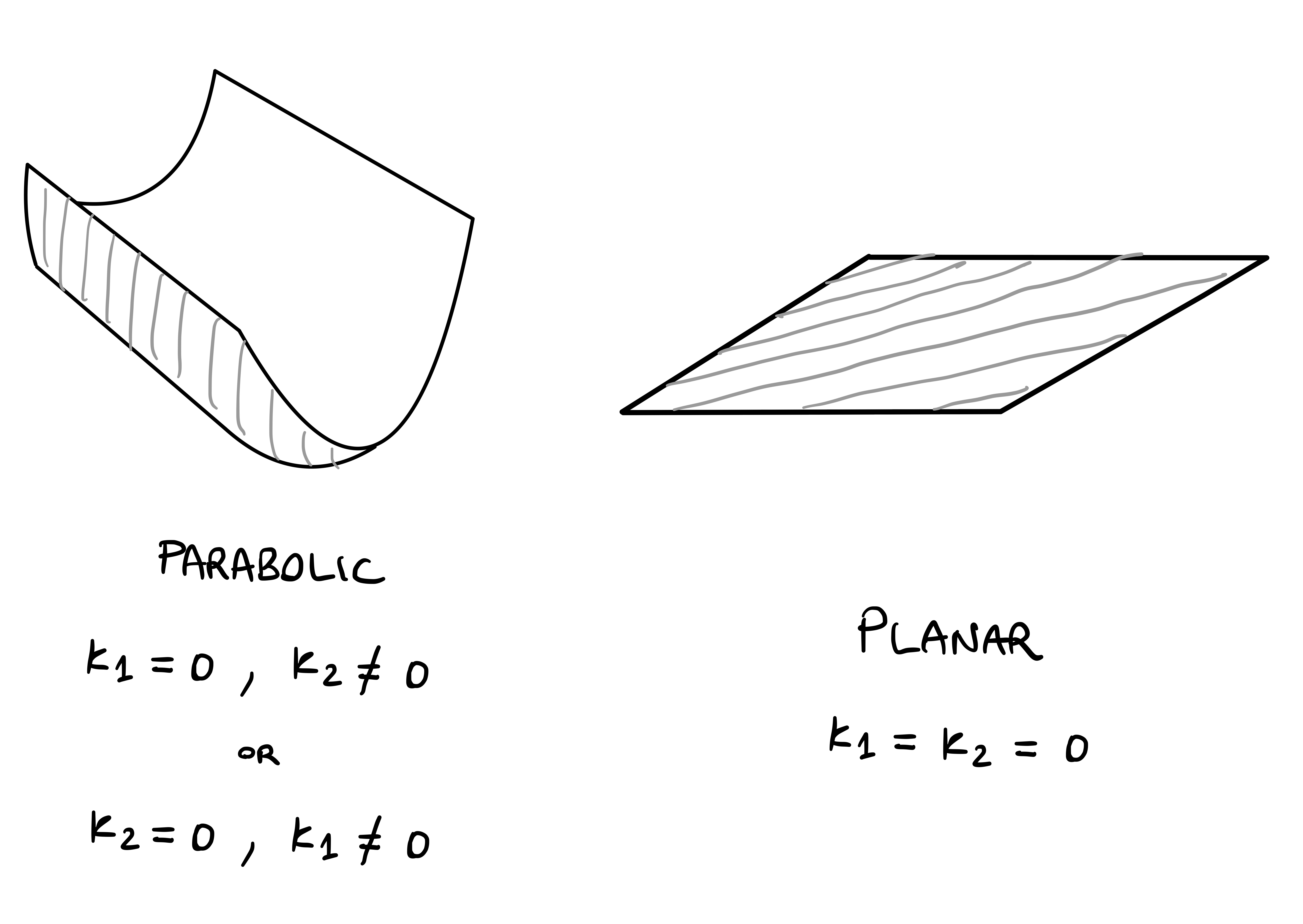
Example 187
Consider the surface chart \[ {\pmb{\sigma}}(u, v) = \left(u-v, u+v, u^{2}+v^{2}\right) \,. \] Show that \(\mathbf{p}= {\pmb{\sigma}}(1,0)\) is an elliptic point. Therefore \({\pmb{\sigma}}\) is approximated by an elliptic paraboiloid in the vicinity of \(\mathbf{p}\).
Solution. In Example 161 we have shown that the Weingarten matrix of \({\pmb{\sigma}}\) is \[ \mathcal{W} = \frac{1}{(1 + 2u^2 + 2v^2)^{\frac32}} \,\left(\begin{array}{ll} 1 + 2v^2 & -2uv \\ - 2uv & 1 + 2u^2 \end{array}\right) \,. \] For \(u=1\) and \(v=1\) we obtain \[ \mathcal{W} = \frac{1}{3^{\frac32}} \,\left(\begin{array}{ll} 1 & 0 \\ 0 & 3 \end{array}\right) = \left(\begin{array}{ll} 3^{-\frac32} & 0 \\ 0 & 3^{- \frac12} \end{array}\right) \,. \] Therefore the principal curvatures at \(\mathbf{p}\) are \[ \kappa_1(\mathbf{p}) = 3^{-\frac32} \,, \quad \kappa_2(\mathbf{p}) = 3^{-\frac12} \,. \quad \] Since \(\kappa_1(\mathbf{p}) > 0\) and \(\kappa_2(\mathbf{p}) > 0\) we have that \(\mathbf{p}\) is an elliptic point.
4.13.5 Umbilical points
Definition 188: Umbilical point
Remark 189
Suppose that \(\mathbf{p}\) is an umbilic, that is, \[ \kappa_1=\kappa_2 \] at \(\mathbf{p}\). Let \(\kappa_n\) be the normal curvature of a unit speed curve \({\pmb{\gamma}}\) passing through \(\mathbf{p}\). By Theorem 182 we have \[ \kappa_n = \kappa_1 \cos^2(\theta) + \kappa_2 \sin^2(\theta) = \kappa_1 \,. \] Therefore \(\kappa_n\) does not depend on \({\pmb{\gamma}}\). Intuitively, this can only happen if in the vicinity of \(\mathbf{p}\) the surface looks like a sphere or a plane. Indeed, the following theorem holds.
Theorem 190
Proof
By assumption we have \[ \kappa_1 (\mathbf{p}) = \kappa_2 (\mathbf{p}) = \kappa (\mathbf{p}) \,, \quad \forall \, \mathbf{p}\in \mathcal{S}\,. \tag{4.25}\]
Step 1. \(\kappa\) is constant.
By Theorem 167 the principal vectors \(\{\mathbf{t}_1,\mathbf{t}_2\}\) are an orthonormal basis of \(T_{\mathbf{p}} \mathcal{S}\). Hence, for each \(\mathbf{v}\in T_{\mathbf{p}} \mathcal{S}\) there exist \(\lambda,\mu \in \mathbb{R}\) such that \[ \mathbf{v}= \lambda \mathbf{t}_1 + \mu \mathbf{t}_2 \,. \] Using the linearity of \(\mathcal{W}_{\mathbf{p},\mathcal{S}}\) and (4.25) we obtain \[\begin{align*} \mathcal{W}_{\mathbf{p},\mathcal{S}} (\mathbf{v}) & = \lambda \mathcal{W}_{\mathbf{p},\mathcal{S}} ( \mathbf{t}_1) + \mu \mathcal{W}_{\mathbf{p},\mathcal{S}} (\mathbf{t}_2) \\ & = \lambda \kappa \mathbf{t}_1 + \mu \kappa \mathbf{t}_2 \\ & = \kappa \mathbf{v}\,, \end{align*}\] showing that \[ \mathcal{W}_{\mathbf{p},\mathcal{S}} (\mathbf{v}) = \kappa \mathbf{v}\,, \quad \forall \, \mathbf{v}\in T_{\mathbf{p}} \mathcal{S}\,. \tag{4.26}\] Let \({\pmb{\sigma}}\colon U \to \mathbb{R}^3\) be a chart of \(\mathcal{S}\). Up to restricting \({\pmb{\sigma}}\), we can assume that \(U\) is connected. By Lemma 158 we have \[ \mathcal{W}_{\mathbf{p},\mathcal{S}} ({\pmb{\sigma}}_u) = - \mathbf{N}_{u} \,, \quad \mathcal{W}_{\mathbf{p},\mathcal{S}} ({\pmb{\sigma}}_v) = - \mathbf{N}_{v} \,. \] On the other hand, by (4.26) we infer \[ \mathcal{W}_{\mathbf{p},\mathcal{S}} ({\pmb{\sigma}}_u) = \kappa {\pmb{\sigma}}_u \,, \quad \mathcal{W}_{\mathbf{p},\mathcal{S}} ({\pmb{\sigma}}_v) = \kappa {\pmb{\sigma}}_v \,, \] from which \[ \mathbf{N}_{u} = - \kappa {\pmb{\sigma}}_u \,, \quad \mathbf{N}_{v} = - \kappa {\pmb{\sigma}}_v \,. \tag{4.27}\] Thus \[ \left( \kappa {\pmb{\sigma}}_u \right)_v = - \left( \mathbf{N}_u \right)_v = - \left( \mathbf{N}_v \right)_u = \left( \kappa {\pmb{\sigma}}_v \right)_u \,. \] Moreover \[\begin{align*} \left( \kappa {\pmb{\sigma}}_u \right)_v & = \kappa_v {\pmb{\sigma}}_u + \kappa {\pmb{\sigma}}_{uv} \\ \left( \kappa {\pmb{\sigma}}_v \right)_u & = \kappa_u {\pmb{\sigma}}_v + \kappa {\pmb{\sigma}}_{uv} \,, \end{align*}\] so that \[ \kappa_v {\pmb{\sigma}}_u = \kappa_u {\pmb{\sigma}}_v \,. \tag{4.28}\] Recall that \({\pmb{\sigma}}_u\) and \({\pmb{\sigma}}_v\) are linearly independent, being \(\mathcal{S}\) regular. Hence the linear combination at (4.28) must be trivial, implying \[ \kappa_u = \kappa_v = 0 \,. \] Since \(U\) is connected, the above implies that \(\kappa\) is constant.
Step 2. We have the two cases \(\kappa = 0\) and \(\kappa \neq 0\).
Assume \(\kappa = 0\). By (4.27) we get that \[ \mathbf{N}_u = \mathbf{N}_v = {\pmb{0}}\,, \] which implies \(\mathbf{N}\) is constant. Therefore \[ \left( \mathbf{N}\cdot {\pmb{\sigma}}\right)_u = \mathbf{N}_u \cdot {\pmb{\sigma}}+ \mathbf{N}\cdot {\pmb{\sigma}}_u = 0 \] since \(\mathbf{N}_u = {\pmb{0}}\) and \(\mathbf{N}\cdot {\pmb{\sigma}}_u = 0\) because \(\mathbf{N}\) is orthogonal to \(T_{\mathbf{p}} \mathcal{S}\). Similarly we get \[ \left( \mathbf{N}\cdot {\pmb{\sigma}}\right)_v = 0 \,, \] showing that \(\mathbf{N}\cdot {\pmb{\sigma}}\) is constant. Hence there exists \(c \in \mathbb{R}\) such that \[ \mathbf{N}\cdot {\pmb{\sigma}}(u,v) = c \,, \quad \forall \, (u,v) \in U \,. \] This shows \({\pmb{\sigma}}(U)\) is contained in the plane \[ \pi = \{ \mathbf{x}\in \mathbb{R}^3 \, \colon \,\mathbf{N}\cdot \mathbf{x}= c \} \,. \]
Assume \(\kappa \neq 0\). Condition (4.27) implies \[ \mathbf{N}= -\kappa {\pmb{\sigma}}+ \mathbf{a} \] for some \(\mathbf{a} \in \mathbb{R}^3\) constant vector. Thus \[ \left\| {\pmb{\sigma}}- \frac{1}{\kappa} \mathbf{a} \right\|^2 = \left\| - \frac{1}{\kappa} \mathbf{N}\right\|^2 = \frac{1}{\kappa^2} \,, \] given that \(\| \mathbf{N}\| = 1\). Therefore \({\pmb{\sigma}}(U)\) is contained in the sphere of center \(\mathbf{a}/\kappa\) and radius \(1/\kappa\).