3 Topology
So far we have worked in \(\mathbb{R}^n\), where for example we have the notions of open set, continuous function and compact set. Topology is what allows us to extend these notions to arbitrary sets.
Definition 1: Topological space
Let \(X\) be a set and \(\mathcal{T}\) a collection of subsets of \(X\). We say that \(\mathcal{T}\) is a topology on \(X\) if the following 3 properties hold:
(A1) We have \(\emptyset, X \in \mathcal{T}\),
(A2) If \(\{A_i\}_{i \in I}\) is an arbitrary family of elements of \(\mathcal{T}\), then \[ \bigcup_{i \in I} A_i \in \mathcal{T}\,. \]
(A3) If \(A,B \in \mathcal{T}\) then \[ A \cap B \in \mathcal{T}\,. \]
Further, we say:
- The pair \((X,\mathcal{T})\) is a topological space.
- The elements of \(X\) are called points.
- The sets in the topology \(\mathcal{T}\) are called open sets.
Remark 2
The intersection property of \(\mathcal{T}\), Property (A3) in Definition 1, is equivalent to the following:
- (A3’) If \(A_1, \ldots, A_M \in \mathcal{T}\) for some \(M \in \mathbb{N}\), then \[ \bigcap_{n=1}^M A_n \in \mathcal{T}\,. \]
The equivalence between (A3) and (A3’) can be immediately obtained by induction.
Warning
Notice:
- The union property (A2) of \(\mathcal{T}\) holds for an arbitrary number of sets, even uncountable!
- The intersection property (A3’) of \(\mathcal{T}\) holds only for a finite number of sets.
There are two main examples of topologies that one should always keep in mind. These are:
- Trivial topology: The topology with the smallest possible number of sets.
- Discrete topology: The topology with the highest possible number of sets.
Definition 3: Trivial topology
Let \(X\) be a set. The trivial topology on \(X\) is the topology \(\mathcal{T}\) defined by \[ \mathcal{T}:= \{ \emptyset , X \} \,. \]
Let us check that \(\mathcal{T}\) is indeed a topology. We need to verify the 3 properties of a topology:
- (A1) We clearly have \(\emptyset , X \in \mathcal{T}\).
- (A2) The only non-trivial union to check is the one between \(\emptyset\) and \(X\). We have \[ \emptyset \cup X = X \in \mathcal{T}\,. \]
- (A3) The only non-trivial intersection to check is the one between \(\emptyset\) and \(X\). We have \[ \emptyset \cap X = \emptyset \in \mathcal{T}\,. \]
Therefore \(\mathcal{T}\) is a topology on \(X\).
Definition 4: Discrete topology
Let \(X\) be a set. The discrete topology on \(X\) is the topology \(\mathcal{T}\) defined by \[ \mathcal{T}:= \{ A \, \colon \,A \subseteq X \} \,, \] that is, every subset of \(X\) is open.
Let us check that \(\mathcal{T}\) is a topology:
(A1) We have \(\emptyset , X \in \mathcal{T}\), since \(\emptyset\) and \(X\) are subsets of \(X\).
(A2) The arbitrary union of subsets of \(X\) is still a subset of \(X\). Therefore \[ \bigcup_{i \in I} A_i \in \mathcal{T}\,, \] whenever \(A_i \in \mathcal{T}\) for all \(i \in I\).
(A3) The intersection of two subsets of \(X\) is still a subset of \(X\). Therefore \[ A \cap B \in \mathcal{T}\,, \] whenever \(A, B \in \mathcal{T}\).
Therefore \(\mathcal{T}\) is a topology on \(X\).
We anticipated that topology is the extension of familiar concepts of open set, continuity, etc. that we have in \(\mathbb{R}^n\). Let us see how the usual definition of open set of \(\mathbb{R}^n\) can fit in our new abstract framework of topology.
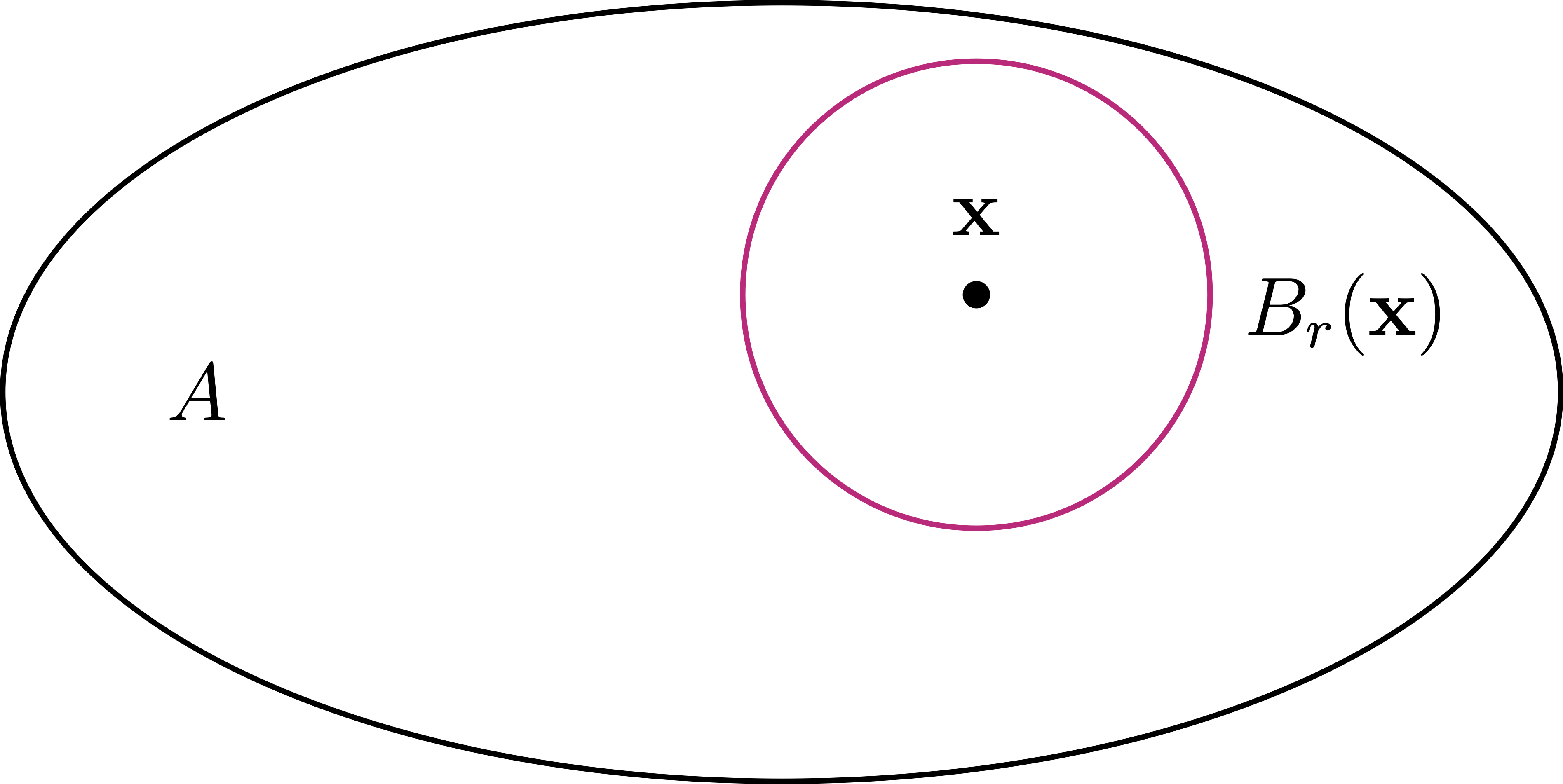
Definition 5: Open set of \(\mathbb{R}^n\)
See Figure 3.1 for a schematic picture of an open set.
Definition 6: Euclidean topology of \(\mathbb{R}^n\)
We need to check that the above definition is well-posed, in the sense that we have to prove that \(\mathcal{T}\) is a topology on \(\mathbb{R}^n\).
Proof: Well-posedness of Definition 6
(A1) We have \(\emptyset , \mathbb{R}^n \in \mathcal{T}\): Indeed \(\emptyset\) is open because there is no point \(\mathbf{x}\) for which (3.1) needs to be checked. Moreover \(\mathbb{R}^n\) is open because (3.1) holds with any radius \(r>0\).
(A2) Let \(A_i \in \mathcal{T}\) for all \(i \in I\) and define the union set \[ A:=\bigcup_{i \in I} A_i \,. \] We need to check that \(A\) is open. Let \(\mathbf{x}\in A\). By definition of union, there exists an index \(i_0 \in I\) such that \(\mathbf{x}\in A_{i_0}\). Since \(A_{i_0}\) is open, by (3.1) there exists \(r>0\) such that \(B_r(\mathbf{x}) \subseteq A_{i_0}\). As \(A_{i_0} \subseteq A\), we conclude that \(B_r(\mathbf{x}) \subseteq A\). Thus \(A\) is open and \(A \in \mathcal{T}\).
(A3) Let \(A, B \in \mathcal{T}\). We need to check that \(A \cap B\) is open. Let \(\mathbf{x}\in A \cap B\). Therefore \(\mathbf{x}\in A\) and \(\mathbf{x}\in B\). Since \(A\) and \(B\) are open, by (3.1) there exist \(r_1,r_2>0\) such that \(B_{r_1}(\mathbf{x}) \subseteq A\) and \(B_{r_2}(\mathbf{x}) \subseteq B\). Set \(r := \min\{ r_1,r_2\}\). Then \[ B_r(\mathbf{x}) \subseteq B_{r_1}(\mathbf{x}) \subseteq A \,, \quad B_r(\mathbf{x}) \subseteq B_{r_2}(\mathbf{x}) \subseteq B \,, \] Hence \(B_r(\mathbf{x}) \subseteq A \cap B\), showing that \(A \cap B\) open, so that \(A \cap B \in \mathcal{T}\).
This proves that \(\mathcal{T}\) is a topology on \(\mathbb{R}^n\).
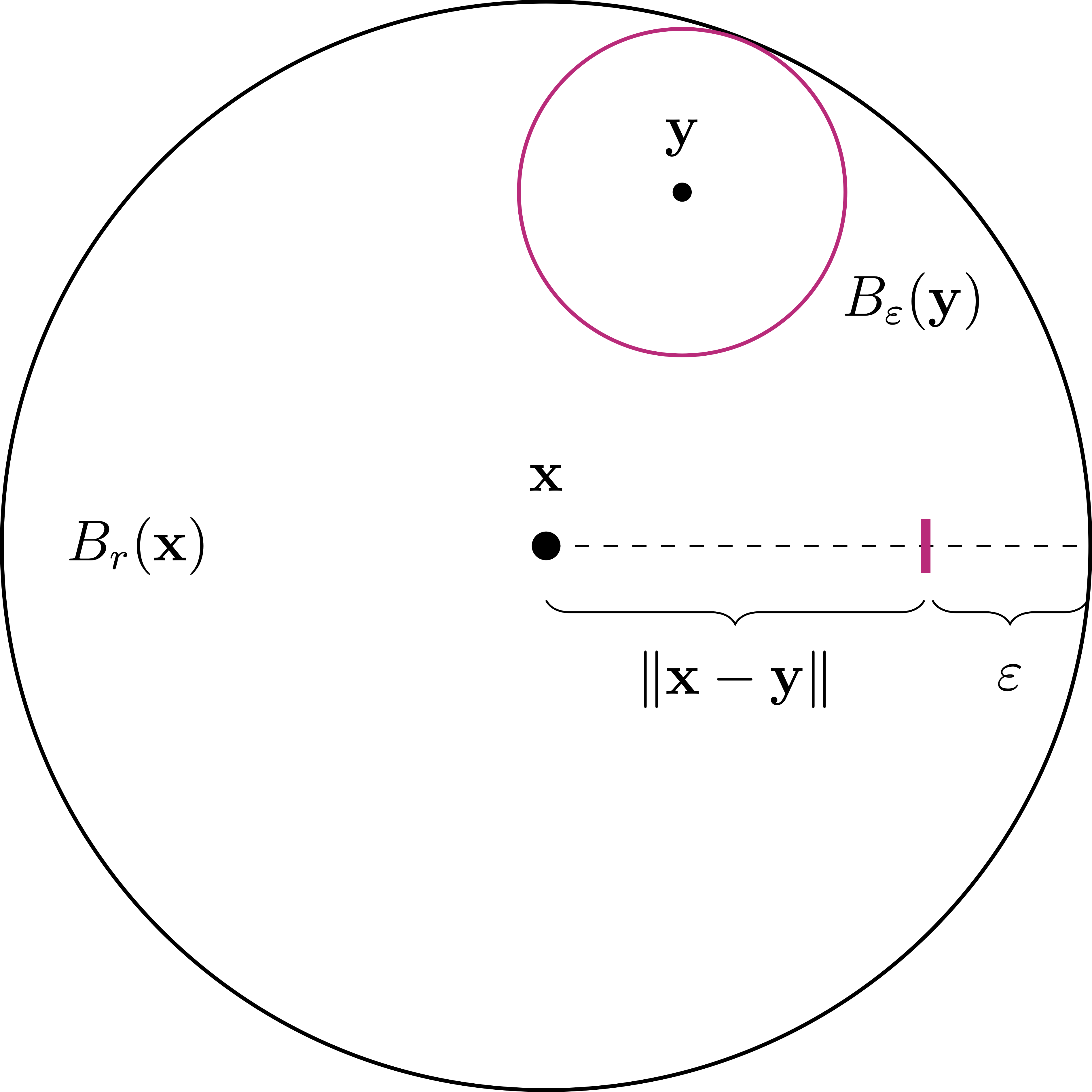
Let us make a basic bus useful observation: balls in \(\mathbb{R}^n\) are open for the Euclidean topology.
Proposition 7
Proof
3.1 Closed sets
The opposite of open sets are closed sets.
Definition 8: Closed set
In words, a set is closed if its complement is open.
Warning
There are sets which are neither open nor closed. For example consider \(\mathbb{R}\) equipped with Euclidean topology. Then the interval \[ A:=[0,1) \] is neither open nor closed.
For the moment we do not have the tools to prove this. We will have them shortly.
We could have defined a topology starting from closed sets. We would have had to replace the properties (A1)-(A2)-(A3) with suitable properties for closed sets. Such properties are detailed in the following proposition.
Proposition 9
Let \((X,\mathcal{T})\) be a topological space. Properties (A1)-(A2)-(A3) of \(\mathcal{T}\) are equivalent to (C1)-(C2)-(C3), where
- (C1) \(\emptyset, X\) are closed.
- (C2) If \(C_i\) is closed for all \(i \in I\), then \[ \bigcap_{i \in I} \, C_i \] is closed.
- (C3) If \(C_1,C_2\) are closed then \[ C_1 \cup C_2 \] is closed.
Proof
We have 3 points to check:
The equivalence between (A1) and (C1) is clear, since \[ \emptyset^c = X \,, \quad X^c = \emptyset \,. \]
Suppose \(C_i\) are closed for all \(i \in I\). Therefore \(C_i^c\) are open for all \(i \in I\). By De Morgan’s laws we have that \[ \left( \bigcap_{i \in I} \, C_i \right)^c = \bigcup_{i \in I} \, C_i^c \] showing that \[ \bigcap_{i \in I} \, C_i \, \mbox{ is closed} \quad \iff \quad \bigcup_{i \in I} \, C_i^c \, \mbox{ is open} \,. \] Therefore (A2) and (C2) are equivalent.
Suppose \(C_1,C_2\) are closed. Therefore \(C_1^c, C_2^c\) are open. By De Morgan’s laws we have that \[ \left( C_1 \cup C_2 \right)^c = C_1^c \cap C_2^c \] showing that \[ C_1 \cup C_2 \, \mbox{ is closed} \quad \iff \quad C_1^c \cap C_2^c \, \mbox{ is open} \,. \] Therefore (A3) and (C3) are equivalent.
As a consequence of the above proposition, we can define a topology by declaring what the closed sets are. We then need to verify that (C1)-(C2)-(C3) are satisfied by such topology. Let us make an example.
Example 10: The Zariski topology
3.2 Comparing topologies
Consider the situation where you have two topologies \(\mathcal{T}_1\) and \(\mathcal{T}_2\) on the same set \(X\). We would like to have some notions of comparison between \(\mathcal{T}_1\) and \(\mathcal{T}_2\).
Definition 11: Finer and coarser topology
- \(\mathcal{T}_1\) is finer than \(\mathcal{T}_2\).
- \(\mathcal{T}_2\) is coarser than \(\mathcal{T}_1\).
If it holds \[ \mathcal{T}_2 \subsetneq \mathcal{T}_1 \,, \] we say that:
- \(\mathcal{T}_1\) is strictly finer than \(\mathcal{T}_2\).
- \(\mathcal{T}_2\) is strictly coarser than \(\mathcal{T}_1\).
We say that \(\mathcal{T}_1\) and \(\mathcal{T}_2\) are the same topology if \[ \mathcal{T}_1 = \mathcal{T}_2 \,. \]
Example 12
Another interesting example is given by the cofinite topology on \(\mathbb{R}\). The sets in this topology are open if they are either empty, or coincide with \(\mathbb{R}\) with a finite number of points removed.
Example 13: Cofinite topology on \(\mathbb{R}\)
Consider the following family \(\mathcal{T}_{\textrm{cofinite}}\) of subsets of \(\mathbb{R}\) \[ \mathcal{T}_{\textrm{cofinite}} := \{ U \subseteq \mathbb{R}\, \colon \,U^c \, \mbox{ is finite, } \mbox{or } U^c = \mathbb{R}\}\,. \] Then \((\mathbb{R},\mathcal{T}_{\textrm{cofinite}})\) is a topological space, and \(\mathcal{T}_{\textrm{cofinite}}\) is called the cofinite topology. We have that \[ \mathcal{T}_{\textrm{cofinite}} \subsetneq \mathcal{T}_{\textrm{euclidean}} \,. \]
Exercise: Show that \(\mathcal{T}_{\textrm{cofinite}}\) is a topology on \(\mathbb{R}\) and that \(\mathcal{T}_{\textrm{cofinite}} \subsetneq \mathcal{T}_{\textrm{euclidean}}\).
3.3 Convergence
We have generalized the notion of open set to arbitrary sets. Next we generalize the notion of convergence of sequences.
Definition 14: Convergent sequence
Notation
Let us analyze the definition of convergence in the topologies we have encountered so far. We will have that:
- Trivial topology: Every sequence converges to every point.
- Discrete topology: A sequence converges if and only if it is eventually constant.
- Euclidean topology: Topological convergence coincides with classical notion of convergence.
We now precisely state and prove the above claims.
Proposition 15: Convergence for trivial topology
Proof
\(U = \emptyset\): This case is not possible, since \(x_0\) cannot be in \(U\).
\(U = X\): Take \(N=1\). Since \(U\) is the whole space, then \(x_n \in U\) for all \(n \geq 1\).
As these are all the open sets, we conclude that \(x_n \to x_0\).
Warning
Proposition 16: Convergence for discrete topology
Let \((X,\mathcal{T})\) be topological space, with \(\mathcal{T}\) the discrete topology, that is, \[ \mathcal{T}= \{ A \, \colon \,A \subseteq X \} \,. \] Let \(\{x_n\} \subseteq X\) be a sequence and \(x_0 \in X\) a point. They are equivalent:
- \(x_n \to x_0\).
- \(\{x_n\}\) is eventually constant, that is, there exists \(N \in \mathbb{N}\) such that \[ x_n = x_0 \,, \quad \forall \, n \geq N \,. \]
Proof
We have to prove that \(\{x_n\}\) is eventually constant. To this end, let \[ U = \{x_0\} \,. \] Then \(U \in \mathcal{T}\). Since \(x_n \to x_0\), by (3.4) there exists \(N \in \mathbb{N}\) such that \[ x_n \in U \,, \quad \forall \, n \geq N \,. \] As \(U = \{x_0\}\), the above is saying that \(x_n = x_0\) for all \(n \geq N\). Hence \(x_n\) is eventually constant.
Part 2. Assume that \(x_n\) is eventually equal to \(x_0\).
By assumption there exists \(N \in \mathbb{N}\) such that \[ x_n = x_0 \,, \quad \forall \, n \geq N \,. \tag{3.5}\] Let \(U \in \mathcal{T}\) be an open set such that \(x_0 \in U\). By (3.5) we have that \[ x_n \in U \,, \quad \forall \, n \geq N \,. \] Since \(U\) was arbitrary, we conclude that \(x_n \to x_0\).
Before proceeding to examining convergence in the Euclidean topology, let us recall the classical definition of convergence in \(\mathbb{R}^n\).
Definition 17: Classical convergence in \(\mathbb{R}^n\)
Proposition 18: Convergence for Euclidean topology
Let \(\mathbb{R}^n\) be equipped with \(\mathcal{T}\) the Euclidean topology. Let \(\{\mathbf{x}_n\} \subseteq \mathbb{R}^n\) be a sequence and \(\mathbf{x}_0 \in \mathbb{R}^n\) a point. They are equivalent:
- \(\mathbf{x}_n \to \mathbf{x}_0\) with respect to \(\mathcal{T}\).
- \(\mathbf{x}_n \to \mathbf{x}_0\) in the classical sense.
Proof
Fix \(\varepsilon>0\) and consider the set \[ U := B_{\varepsilon}(\mathbf{x}_0) \,. \] By Proposition 7 we know that \(U \in \mathcal{T}\). Moreover \(\mathbf{x}_0 \in U\). By the convergence \(\mathbf{x}_n \to \mathbf{x}_0\) with respect to \(\mathcal{T}\), there exists \(N \in \mathbb{N}\) such that \[ \mathbf{x}_n \in U \,, \quad \forall \, n \geq N \,. \] As \(U = B_{\varepsilon}(\mathbf{x}_0)\), the above reads \[ \left\| \mathbf{x}_n - \mathbf{x}_0 \right\| < \varepsilon\,, \quad \forall \, n \geq N \,, \] showing that \(\mathbf{x}_n \to \mathbf{x}_0\) in the classical sense.
Part 2. Assume \(\mathbf{x}_n \to \mathbf{x}_0\) in the classical sense.
Let \(U \in \mathcal{T}\) be such that \(\mathbf{x}_0 \in U\). By definition of Euclidean topology, this means that there exists \(r>0\) such that \[ B_r(\mathbf{x}_0) \subseteq U \,. \] As \(\mathbf{x}_n \to \mathbf{x}_0\) in the classical sense, there exists \(N \in \mathbb{N}\) such that \[ \left\| \mathbf{x}_n - \mathbf{x}_0 \right\| < r \,, \quad \forall \, n \geq N \,. \] The above is equivalent to \[ \mathbf{x}_n \in B_{r}(\mathbf{x}_0) \,, \quad \forall \, n \geq N \,. \] Since \(B_r(\mathbf{x}_0) \subseteq U\), we have proven that \[ \mathbf{x}_n \in U \,, \quad \forall \, n \geq N \,. \] Since \(U\) is arbitrary, we conclude that \(\mathbf{x}_n \to \mathbf{x}_0\) with respect to \(\mathcal{T}\).
Notation
We conclude with a useful proposition which relates convergences when multiple topologies are present.
Proposition 19
Proof
3.4 Metric spaces
We will now define a class of topological spaces known as metric spaces.
Definition 20: Distance
Let \(X\) be a set. A distance on \(X\) is a function \[ d \colon X \times X \to \mathbb{R} \] such that, for all \(x,y,z \in X\) they hold:
(M1) Positivity: The distance is non-negative \[ d(x,y) \geq 0 \,. \] Moreover \[ d(x,y) = 0 \quad \iff x=y \,. \]
(M2) Symmetry: The distance is symmetric \[ d(x,y) = d(y,x) \,. \]
(M3) Triangle Inequality: It holds \[ d(x,z) \leq d(x,y) + d(y,z) \,. \]
Definition 21: Metric space
Example 22: \(\mathbb{R}^n\) as metric space
The Euclidean norm naturally induces a distance over \(\mathbb{R}^n\) by setting \[ d(\mathbf{x},\mathbf{y}) := \left\| \mathbf{x}- \mathbf{y} \right\| \,. \] Then \((\mathbb{R}^n,d)\) is a metric space.
It is trivial to check that the Euclidean distance satisfies (M1) and (M2). To show (M3), recalling the triangle inequality in \(\mathbb{R}^n\): \[ \| \mathbf{x}+ \mathbf{y}\| \leq \| \mathbf{x}\| + \| \mathbf{y}\| \,, \] for all \(\mathbf{x}, \mathbf{y}\in \mathbb{R}^n\). Using the above we obtain \[\begin{align*} d(\mathbf{x},\mathbf{y}) & = \| \mathbf{x}- \mathbf{y}\| \\ & = \| (\mathbf{x}- \mathbf{z}) + (\mathbf{z}- \mathbf{y}) \| \\ & \leq \| \mathbf{x}- \mathbf{z}\| + \| \mathbf{z}- \mathbf{y}\| \\ & = d (\mathbf{x},\mathbf{z}) + d (\mathbf{z},\mathbf{y}) \,, \end{align*}\] proving that \(d\) satisfies (M3). This prove that \((\mathbb{R}^n,d)\) is a metric space.
Example 23: \(p\)-distance on \(\mathbb{R}^n\)
For \(\mathbf{x},\mathbf{y}\in \mathbb{R}^n\) and \(p \in [1,\infty)\) define \[ d_p ( \mathbf{x}, \mathbf{y}) := \left( \sum_{i=1}^n |x_i - y_i|^p \right)^{\frac1p} \,. \] Note that \(d_2\) coincides with the Euclidean distance. For \(p = \infty\) we set \[ d_{\infty} ( \mathbf{x}, \mathbf{y}) := \max_{i = 1 \ldots, n} |x_i - y_i| \,. \] We have that \((\mathbb{R}^n,d_p)\) is a metric space.
Indeed properties (M1)-(M2) hold trivially. The triangle inequality is also trivially satisfied by \(d_{\infty}\). We are left with checking the triangle inequality for \(d_p\) with \(p \geq 1\). To this end, define \[ \| \mathbf{x}\|_p := \left( \sum_{i=1}^n |x_i|^p \right)^{\frac1p} \,. \] Minkowski’s inequality, see Wikipedia page, states that \[ \| \mathbf{x}+ \mathbf{y}\|_p \leq \| \mathbf{x}\|_p + \| \mathbf{y}\|_p \,, \] for all \(\mathbf{x},\mathbf{y}\in \mathbb{R}^n\). Therefore \[\begin{align*} d_p(\mathbf{x},\mathbf{y}) & = \| \mathbf{x}- \mathbf{y}\|_p \\ & = \| (\mathbf{x}- \mathbf{z}) + (\mathbf{z}- \mathbf{y}) \|_p \\ & \leq \| \mathbf{x}- \mathbf{z}\|_p + \| \mathbf{z}- \mathbf{y}\|_p \\ & = d_p (\mathbf{x},\mathbf{z}) + d_p (\mathbf{z},\mathbf{y}) \,, \end{align*}\] proving that \(d_p\) satisfies (M3). Hence \((\mathbb{R}^n,d_p)\) is a metric space.
A metric \(d\) on a set \(X\) naturally induces a topology which is compatible with the metric.
Definition 24: Topology induced by the metric
We need to check that the above definition is well-posed, that is, we need to show that \(\mathcal{T}_d\) is actually a topology on \(X\). The proof follows, line by line, the proof that the Euclidean topology is indeed a topology, see proof immediately below Definition 6. This is left as an exercise.
Example 25: Topology induced by Euclidean distance
Consider the metric space \((\mathbb{R}^n,d)\) with \(d\) the Euclidean distance. Then \[ \mathcal{T}_d = \mathcal{T}_{\textrm{euclidean}} \,, \] where \(\mathcal{T}_{\textrm{euclidean}}\) is the Euclidean topology on \(\mathbb{R}^n\).
Exercise: Prove the above statement. It is an immediate consequence of definitions.
Example 26: Discrete distance
Let \(X\) be a set. Define the function \(d \colon X \times X \to \mathbb{R}\) by \[ d(x,y) := \begin{cases} 0 & \mbox{ if } \, x = y \\ 1 & \mbox{ if } \, x \neq y \end{cases} \] Then \((X,d)\) is a metric space, and \(d\) is called the discrete distance. Moreover \[ \mathcal{T}_d = \mathcal{T}_{\textrm{discrete}} \] where \(\mathcal{T}_{\textrm{discrete}}\) is the discrete topology on \(X\).
Exercise: Prove that \((X,d)\) is a metric space and \(\mathcal{T}_d = \mathcal{T}_{\textrm{discrete}}\).
The following proposition tells us that balls in a metric space \(X\) are open sets. Moreover balls are the building blocks of all open sets in \(X\). The proof is left as an exercise.
Proposition 27
Let \((X,d)\) be a metric space and \(\mathcal{T}_d\) the topology induced by \(d\). Then:
- For all \(x \in X\), \(r>0\) we have \(B_r(x) \subseteq \mathcal{T}_d\).
- \(U \in \mathcal{T}_d\) if and only if \[ U = \bigcup_{ i \in I } B_{r_i}(x_i) \,, \] with \(I\) family of indices and \(x_i \in X\), \(r_i > 0\).
We now define the concept of equivalent metrics.
Definition 28: Equivalent metrics
The following proposition gives a sufficent condition for the equivalence of two metrics.
Proposition 29
The proof of Proposition 29 is trivial, and is left as an exercise.
Example 30
Let \(p > 1\). The metrics \(d_p\) and \(d_{\infty}\) on \(\mathbb{R}^n\) are equivalent.
This follows from Proposition 29 and the estimate \[ d_{\infty} (\mathbf{x},\mathbf{y}) \leq d_p (\mathbf{x},\mathbf{y}) \leq n \, d_{\infty} (\mathbf{x},\mathbf{y}) \,, \quad \forall \mathbf{x}\,, \, \mathbf{y}\in \mathbb{R}^n \,. \]
Warning
We can characterize the convergence of sequences in metric spaces.
Proposition 31: Convergence in metric space
Suppose \((X,d)\) is a metric space and denote by \(\mathcal{T}_d\) the topology induce by \(d\). Let \(\{x_n\} \subseteq X\) and \(x_0 \in X\). They are equivalent:
- \(x_n \to x_0\) with respect to the topology \(\mathcal{T}_d\).
- \(d(x_n,x_0) \to 0\) in \(\mathbb{R}\).
- For all \(\varepsilon>0\) there exists \(N \in \mathbb{N}\) such that \[ x_n \in B_r(x_0) \, , \,\, \forall \, n \geq \mathbb{N}\,. \]
The proof is similar to the one of Proposition 18, and it is left as an exercise.
3.5 Interior, closure and boundary
We now define interior, closure and boundary of a set \(A\) contained in a topological space.
Definition 32: Interior of a set
Remark 33
Proposition 34
Let \((X,\mathcal{T})\) be a topological space and \(A \subseteq X\) a set. Then \(\mathop{\mathrm{Int}}{A}\) is the largest open set contained in \(A\), that is:
- \(\mathop{\mathrm{Int}}{A}\) is open.
- \(\mathop{\mathrm{Int}}{A} \subseteq A\).
- If \(V \in \mathcal{T}\) and \(V \subseteq A\), then \(V \subseteq \mathop{\mathrm{Int}}{A}\).
- \(A\) is open if and only if \[ A = \mathop{\mathrm{Int}}{A} \,. \]
Proof
We have:
\(\mathop{\mathrm{Int}}{A}\) is open, since it is union of open sets, see property (A2).
\(\mathop{\mathrm{Int}}{A} \subseteq A\), since \(\mathop{\mathrm{Int}}{A}\) is union of sets contained in \(A\).
Suppose \(V \in \mathcal{T}\) and \(V \subseteq A\). Therefore \[ V \subseteq \bigcup_{ \substack{U \subseteq A \\ U \in \mathcal{T}} } \, U = \mathop{\mathrm{Int}}{A} \,. \]
Suppose that \(A\) is open. Then \[ A \subseteq \bigcup_{ \substack{U \subseteq A \\ U \in \mathcal{T}} } \, U = \mathop{\mathrm{Int}}{A} \,. \] As we already know that \(\mathop{\mathrm{Int}}{A} \subseteq A\), we conclude that \(A = \mathop{\mathrm{Int}}{A}\).
Conversely, suppose that \(A = \mathop{\mathrm{Int}}{A}\). Since \(\mathop{\mathrm{Int}}{A}\) is open, then also \(A\) is open.
Definition 35: Closure of a set
Remark 36
Proposition 37
Let \((X,\mathcal{T})\) be a topological space and \(A \subseteq X\) a set. Then \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\) is the smallest closed set containing \(A\), that is:
- \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\) is closed.
- \(A \subseteq {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\).
- If \(V\) is closed \(A \subseteq V\), then \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} \subseteq V\).
- \(A\) is closed if and only if \[ A = {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} \,. \]
Proof
We have:
\({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\) is closed, since it is intersection of closed sets, see property (C2).
\(A \subseteq {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\), since \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\) is intersection of sets which contain \(A\).
Suppose \(V\) is closed and \(A \subseteq V\). Therefore \[ {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} = \bigcap_{ \substack{A \subseteq C \\ C \, \text{closed} } } \, C \subseteq V \,. \]
Suppose that \(A\) is closed. Then \[ {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} = \bigcap_{ \substack{A \subseteq C \\ C \, \text{closed}} } \, C \subseteq A \,, \] showing that \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} \subseteq A\). As we already know that \(A \subseteq {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\), we conclude that \(A = {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\).
Conversely, suppose that \(A = {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\). Since \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\) is closed, then also \(A\) is closed.
Lemma 38
Let \((X,\mathcal{T})\) be a topological space and \(A \subseteq X\) a set. They are equivalent:
- \(x_0 \in {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\).
- For every \(U \in \mathcal{T}\) such that \(x_0 \in U\), it holds \[ U \cap A \neq \emptyset \,. \]
Proof
We prove the contronominal statement: \[ x_0 \notin {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} \quad \iff \quad \exists \,\, U \in \mathcal{T}\, \text{ s.t. } \, x_0 \in U \,, \,\, \, U \cap A = \emptyset \,. \]
Let us check the two implications hold:
Suppose \(x_0 \notin {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\). Then \(x_0 \in U := ({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {})^c\). Note that \(U\) is open, since \(U^c = {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\) is closed. We have \[ A \cap U = A \cap (\overline{A})^c = \emptyset \,, \] since \(A \subseteq {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\).
Assume there exists \(U \in \mathcal{T}\) such that \(x_0 \in U\) and \(U \cap A = \emptyset\). Therefore \(A \subseteq U^c\). Since \(U\) is open, \(U^c\) is closed. Then \[ {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} = \bigcap_{ \substack{ A \subseteq C \\ C \, \text{closed} } } \, C \subseteq U^c \,. \] Since \(x_0 \notin U^c\), we conclude that \(x_0 \notin {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\).
Definition 39: Boundary of a set
Proposition 40
Proof
We can characterize \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\) as the set of limit points of sequences in \(A\).
Definition 41
Proposition 42
Proof
Warning
Example 43: Co-countable topology
Let \(X=\mathbb{R}\) with the co-countable topology \[ \mathcal{T}:= \{ A \subseteq \mathbb{R}\, \colon \,A^c = \mathbb{R}\,\, \mbox{ or } \,\, A^c \, \mbox{ countable }\} \,. \] The set \[ A = (-\infty,0] \] is not closed and \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} = \mathbb{R}\). Moreover, convergent sequences in \((X,\mathcal{T})\) are eventually constant. Therefore \(L(A) = A\), showing that \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} \not\subset L(A)\).
Exercise: Prove all the above statements.
In metric spaces we can characterize the interior of a set and the closure in the following way.
Proposition 44
Proof
Example 45
Consider \(\mathbb{R}\) with the Euclidean topology and \(A :=[0,1)\). We have that \[ \mathop{\mathrm{Int}}{A} = (0,1) \,, \quad {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} = [0,1] \,, \quad \partial A = \{0,1\} \,. \] In particular \[ \mathop{\mathrm{Int}}{A} \neq A \,, \quad {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} \neq A \,, \] showing that \(A\) is neither open, nor closed.
The proof of the above statements is left as an exercise.
3.6 Density
Definition 46: Density
Density can be characterized in terms of closure.
Proposition 47
Let \((X,\mathcal{T})\) be a topological space and \(A \subseteq X\) a set. They are equivalent:
- \(A\) is dense in \(X\).
- It holds \[ {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} = X \,. \]
Proof
Part 2. Suppose that \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} = X\). Let \(U \in \mathcal{T}\) with \(U \neq \emptyset\). By contradiction, assume that \[ A \cap U = \emptyset \,. \] Therefore \(A \subseteq U^c\). As \(U^c\) is closed, we have \[ {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} \subseteq U^c\,, \] because \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\) is the smallest closed set containing \(A\). Recalling that \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} = X\), we conclude that \(U^c = X\). Therefore \(U = \emptyset\), which is a contradiction.
Example 48
Consider \(\mathbb{R}\) with the Euclidean topology.
We have that the set of integers \(\mathbb{Z}\) is closed in \(\mathbb{R}\). Indeed, \[ \mathbb{Z}^c = \bigcup_{ z \in \mathbb{Z}} \, (z , z + 1 ) \,. \] Since \((z,z+1)\) is open in \(\mathbb{R}\), by (A2) we conclude that \(\mathbb{Z}^c\) is open, so that \(\mathbb{Z}\) is closed. Therefore \[ {}\mkern 2mu \overline{\mkern-2mu \mathbb{Z} \mkern-2mu}\mkern 2mu {} = \mathbb{Z}\,, \] showing that \(\mathbb{Z}\) is not dense in \(\mathbb{R}\).
The rational numbers \(\mathbb{Q}\) are instead dense in \(\mathbb{R}\), as proven in the Analysis module. Therefore \[ {}\mkern 2mu \overline{\mkern-2mu \mathbb{Q} \mkern-2mu}\mkern 2mu {} = \mathbb{R}\,. \] It is also easy to check that \[ \mathop{\mathrm{Int}}{\mathbb{Q}} = \emptyset \,. \] Therefore \[ \mathop{\mathrm{Int}}{\mathbb{Q}} \neq \mathbb{Q}\,, \quad {}\mkern 2mu \overline{\mkern-2mu \mathbb{Q} \mkern-2mu}\mkern 2mu {} \neq \mathbb{Q}\,, \] showing that \(\mathbb{Q}\) is neither open, nor closed.
Example 49
Consider \(\mathbb{R}\) with the cofinite topology \[ \mathcal{T}_{\textrm{cofinite}} := \{ U \subset \mathbb{R}\, \colon \,U^c \, \mbox{ is finite, } \mbox{ or } U^c = \mathbb{R}\}\,. \] We have that \[ {}\mkern 2mu \overline{\mkern-2mu \mathbb{Z} \mkern-2mu}\mkern 2mu {} = \mathbb{R}\,, \] showing that \(\mathbb{Z}\) is dense in \(\mathbb{R}\).
Proof. Suppose \(C\) is a closed set such that \(\mathbb{Z}\subseteq C\). By definition of \(\mathcal{T}_{\textrm{cofinite}}\) we have \(C = \mathbb{R}\) or \(C\) finite. Since \(\mathbb{Z}\subseteq C\) and \(\mathbb{Z}\) is not finite, we conclude \(C = \mathbb{R}\). This proves that \(\mathbb{R}\) is the only closed set containing \(\mathbb{Z}\), and so \({}\mkern 2mu \overline{\mkern-2mu \mathbb{Z} \mkern-2mu}\mkern 2mu {} = \mathbb{R}\).
3.7 Hausdorff spaces
Hausdorff space are topological spaces in which points can be separated by means of disjoint open sets.
Definition 50
The main example of Hausdorff spaces are metrizable spaces.
Proposition 51
Proof
In general, every metrizable space is Hausdorff.
Definition 52: Metrizable space
Corollary 53
Proof
As a conseuqence of Corollary 53 we have that spaces which are not metrizable are not Hausdorff. Let us make a few examples.
Example 54: Trivial topology is not Hausdorff
Let \((X,\mathcal{T})\) be a topological space with \(\mathcal{T}\) trivial topology. Assume that \(X\) has more than one element. Then \(X\) is not Hausdorff.
Indeed, let \(x,y \in X\) with \(x \neq y\). Suppose by contradiction that \(X\) is Hausdorff. Then there exist \(U,V \in \mathcal{T}\) such that \[ x \in U \,, \quad y \in V \,, \quad U \cap V = \emptyset \,. \] Recall that \[ \mathcal{T}= \{ \emptyset, X \} \,. \] Since \(x \in U\) and \(y \in V\), we deduce that \(U\) and \(V\) are non-empty. Since \(U\) and \(V\) are open, the only possibility is that \[ U = V = X \,. \] In this case we have \[ U \cap V = X \cap X = X \neq \emptyset \,, \] leading to a contradiciton. Hence \(X\) is not Hausdorff.
Example 55: Cofinite topology on \(\mathbb{R}\)
Consider the following family \(\mathcal{T}\) of subsets of \(\mathbb{R}\) \[ \mathcal{T}:= \{ U \subseteq \mathbb{R}\, \colon \,U^c \, \mbox{ is finite, } \mbox{or } U^c = \mathbb{R}\}\,. \] Then \((\mathbb{R},\mathcal{T})\) is a topological space which is not Hausdorff. The topology \(\mathcal{T}\) is called the cofinite topology.
Exercise: Show that \((\mathbb{R},\mathcal{T})\) is not Hausdorff.
Example 56
Consider the following family \(\mathcal{T}\) of subsets of \(\mathbb{R}\) \[ \mathcal{T}:= \{ U = (-\infty,a) \, \colon \,- \infty \leq a \leq \infty \}\,. \] Then \((\mathbb{R},\mathcal{T})\) is a topological space which is not Hausdorff.
We start by showing that \((\mathbb{R},\mathcal{T})\) is a topological space. We need to check the properties of topologies:
(A1) We have that \[ (\infty,\infty) = \emptyset \in \mathcal{T}\,, \quad (-\infty,\infty) = \mathbb{R}\in \mathcal{T}\,. \]
(A2) Suppose that \(A_i \in \mathcal{T}\) for all \(i \in I\). By definition \[ A_i = (-\infty, a_i) \,, \quad - \infty \leq a_i \leq \infty \,. \] Set \[ a := \sup_{i \in I} \ a_i \,, \quad A := (-\infty, a) \,. \] Note that \(a\) always exists, and possibly \(a=\infty\). Moreover \(A \in \mathcal{T}\). We claim \[ A = \bigcup_{i \in I} \, A_i \,. \tag{3.8}\] To prove (3.8) first suppose that \(x \in A\). Then \(x < a\). Set \(\varepsilon:= a - x\), so that \(\varepsilon>0\). By definition of supremum there exists \(i_{0} \in I\) such that \[ a - \varepsilon< a_{i_0} \,. \] From the above, and from the definition of \(\varepsilon\), we deduce \[ a_{i_0} > a - \varepsilon= a - a + x = x \,, \] showing that \(x \in (-\infty, a_{i_0}) = A_{i_0}\). Therefore \[ A \subseteq \bigcup_{i \in I} \, A_i \,. \] Conversely, assume that \(x \in \cup_{i \in I} \, A_i\). Therefore there exists \(i_0 \in I\) such that \(x \in A_{i_0} = (-\infty, a_{i_0})\). In particular \[ x < a_{i_0} \leq \sup_{i \in I} a_i = a \,, \] showing that \(x \in (-\infty,a) = A\). Therefore \[ \bigcup_{i \in I} \, A_i \subseteq A\,, \] and (3.8) is proven.
(A3) Let \(A, B \in \mathcal{T}\). Therefore \[ A = (-\infty, a)\,, \quad B = (-\infty, b)\,, \] for some \(a,b \in [-\infty, \infty]\). Set \[ U := A \cap B \,, \quad z:= \min \{a,b\} \,. \] It is immediate to check that \[ U = (-\infty, z) \,, \] showing that \(U \in \mathcal{T}\).
Therefore \((\mathbb{R},\mathcal{T})\) is a topological space. We now show that \((\mathbb{R},\mathcal{T})\) is not Hausdorff. Suppose by contradiction that \((\mathbb{R},\mathcal{T})\) is Hausdorff. Let \(x,y \in \mathbb{R}\) with \(x \neq y\). By assumption there exist \(U,V \in \mathcal{T}\) such that \[ x \in U \,, \quad y \in V \,, \quad U \cap V = \emptyset \,. \] By definition of \(\mathcal{T}\) there exist \(a,b \in [-\infty,\infty]\) such that \[ U = (-\infty,a) \,, \quad V = (- \infty, b) \,. \] Since \(x \in U\) and \(y \in V\), in particular \(U\) and \(V\) are non-empty. Therefore \(a,b>-\infty\). Set \[ z := \min\{a , b \}\,, \quad Z:= U \cap V = (-\infty,z) \,. \] As \(a,b>-\infty\), we have \(z > - \infty\). Therefore \(Z \neq \emptyset\). This is a contradiction, since \(U \cap V = \emptyset\). Therefore \((\mathbb{R},\mathcal{T})\) is not Hausdorff.
In Hausdorff spaces the limit of a sequence is unique.
Proposition 57: Uniqueness of limit in Hausdorff spaces
Proof
3.8 Continuity
We extend the notion of continuity to topological spaces. To this end, we need the concept of pre-image of a set under a function.
Definition 58: Images and Pre-images
Let \(X, Y\) be sets and \(f \colon X \to Y\) be a function.
Let \(U \subseteq X\). The image of \(U\) under \(f\) is the subset of \(Y\) defined by \[ f (U) := \{ y \in Y \, \colon \,\exists \, x \in X \, \text{ s.t. } \, y = f(x) \} = \{ f(x) \, \colon \,x \in X \} \,. \]
Let \(V \subseteq Y\). The pre-image of \(V\) under \(f\) is the subset of \(X\) defined by \[ f^{-1} (V) := \{ x \in X \, \colon \,f(x) \in V \} \,. \]
Warning
Let us gather useful properties of images and pre-images.
Proposition 59
- \(A \subseteq f^{-1}(f(A))\)
- \(A = f^{-1}(f(A))\) if \(f\) is injective
- \(f(f^{-1}(B)) \subseteq B\)
- \(f(f^{-1}(B)) = B\) if \(f\) is surjective
- If \(A_1 \subseteq A_2\) then \(f(A_1) \subseteq f(A_2)\)
- If \(B_1 \subseteq B_2\) then \(f^{-1}(B_1) \subseteq f^{-1}(B_2)\)
- If \(A_i \subseteq X\) for \(i \in I\) we have \[\begin{gather*} f \left( \bigcup_{i \in I} A_i \right) = \bigcup_{i \in I} f(A_i) \\ f \left( \bigcap_{i \in I} A_i \right) \subseteq \bigcap_{i \in I} f(A_i) \end{gather*}\]
- If \(B_i \subseteq Y\) for \(i \in I\) we have \[\begin{gather*} f^{-1} \left( \bigcup_{i \in I} B_i \right) = \bigcup_{i \in I} f^{-1}(B_i) \\ f^{-1} \left( \bigcap_{i \in I} B_i \right) = \bigcap_{i \in I} f^{-1}(B_i) \end{gather*}\]
Suppose \(Z\) is another set and \(g \colon Y \to Z\). Let \(C \subseteq Z\). Then \[\begin{align*} & (g \circ f)(A) = g(f(A)) \\ & (g \circ f)^{-1}(C) = f^{-1}(g^{-1}(C)) \end{align*}\]
It is a good exercise to try and prove a few of the above properties. We omit the proof. We can now define continuous functions between topological spaces.
Definition 60: Continuous function
Let \((X,\mathcal{T}_X)\) and \((Y,\mathcal{T}_Y)\) be topological spaces. Let \(f \colon X \to Y\) be a function.
Let \(x_0 \in X\). We say that \(f\) is continuous at \(x_0\) if it holds: \[ \forall \, V \in \mathcal{T}_Y \, \text{ s.t. } \, f(x_0) \in V \,, \,\, \exists \, U \in \mathcal{T}_X \, \text{ s.t. } \, x_0 \in U \,, \,\, f(U) \subseteq V \,. \]
We say that \(f\) is continuous from \((X,\mathcal{T}_X)\) to \((Y,\mathcal{T}_Y)\) if \(f\) is continuous at each point \(x_0 \in X\).
The following proposition presents a useful characterization of continuous functions in terms of pre-images.
Proposition 61
Let \((X,\mathcal{T}_X)\) and \((Y,\mathcal{T}_Y)\) be topological spaces. Let \(f \colon X \to Y\) be a function. They are equivalent:
- \(f\) is continuous from \((X,\mathcal{T}_X)\) to \((Y,\mathcal{T}_Y)\).
- It holds: \[ f^{-1}(V) \in \mathcal{T}_X \,, \quad \forall \, V \in \mathcal{T}_Y \,. \]
Important
The proof of Proposition 61 is simple, but very tedious. We choose to skip it.
Example 62
Let \(X\) be a set and \(\mathcal{T}_1\), \(\mathcal{T}_2\) be topologies on \(X\). Define the identity map \[ {\mathop{\mathrm{Id}}}_{X} \colon (X,\mathcal{T}_1) \to (X,\mathcal{T}_2) \,, \quad {\mathop{\mathrm{Id}}}_{X} (x):= x \,. \] They are equivalent:
- \({\mathop{\mathrm{Id}}}_{X}\) is continuous from \((X,\mathcal{T}_1)\) to \((X,\mathcal{T}_2)\).
- \(\mathcal{T}_1\) is finer than \(\mathcal{T}_2\) \[ \mathcal{T}_2 \subseteq \mathcal{T}_1 \,. \]
Indeed, \({\mathop{\mathrm{Id}}}_{X}\) is continuous if and only if \[ {\mathop{\mathrm{Id}}}_{X}^{-1} (V) \in \mathcal{T}_1 \,, \quad \forall \, V \in \mathcal{T}_2 \,. \] But \({\mathop{\mathrm{Id}}}_{X}^{-1} (V) = V\), so that the above reads \[ V \in \mathcal{T}_1 \,, \quad \forall \, V \in \mathcal{T}_2 \,, \] which is equivalent to \(\mathcal{T}_2 \subseteq \mathcal{T}_1\).
Let us compare our new definition of contiuity with the classical notion of continuity in \(\mathbb{R}^n\). Let us recall the definition of continuous function in \(\mathbb{R}^n\).
Definition 63: Continuity in the classical sense
Proposition 64
Let \(f \colon \mathbb{R}^n \to \mathbb{R}^m\) and suppose \(\mathbb{R}^n,\mathbb{R}^m\) are equipped with the Euclidean topology. Let \(\mathbf{x}_0 \in \mathbb{R}^n\). They are equivalent:
- \(f\) is continuous at \(\mathbf{x}_0\) in the topological sense.
- \(f\) is continuous at \(\mathbf{x}_0\) in the classical sense.
Proof
Part 2. Suppose \(f\) is continuous at \(x_0\) in the classical sense. Let \(V \subset \mathbb{R}^m\) be open and such that \(f(\mathbf{x}_0) \in V\). Since \(V\) is open, there exists \(\varepsilon>0\) such that \[ B_{\varepsilon} (f(\mathbf{x}_0)) \subset V \,. \tag{3.10}\] Since \(f\) is continous in the classical sense, there exists \(\delta>0\) such that \[ \| \mathbf{x}- \mathbf{x}_0 \| < \delta \quad \implies \|f(\mathbf{x}) - f(\mathbf{x}_0)\|< \varepsilon\,. \] The above is equivalent to \[ \mathbf{x}\in B_{\delta}(\mathbf{x}_0) \quad \implies \quad f(\mathbf{x}) \in B_{\varepsilon} (f (\mathbf{x}_0)) \,. \tag{3.11}\] Set \[ U:= B_{\delta}(\mathbf{x}_0) \] and note that \(U\) is open in \(\mathbb{R}^n\) and \(\mathbf{x}_0 \in U\). By definition of image of a set, (3.11) reads \[ f(U) = f( B_{\delta}(\mathbf{x}_0)) \subseteq B_{\varepsilon} (f(\mathbf{x}_0)) \,. \] Recalling (3.10) we conclude that \[ f(U) \subset V \,. \] In summary, we have shown that given \(V \subset \mathbb{R}^m\) open and such that \(f(\mathbf{x}_0) \in V\), there exists \(U\) open in \(\mathbb{R}^n\) such that \(\mathbf{x}_0 \in U\) and \(f(U) \subset V\). Therefore \(f\) is continuous at \(\mathbf{x}_0\) in the topological sense.
A similar proof yields the characterization of continuity in metric spaces. The proof is left as an exercise.
Proposition 65
Let \((X,d_X)\) and \((Y,d_Y)\) be metric spaces. Denote by \(\mathcal{T}_X\) and \(\mathcal{T}_Y\) the topologies induced by the metrics. Let \(f \colon X \to Y\) and \(x_0 \in X\). They are equivalent:
- \(f\) is continuous at \(x_0\) in the topological sense.
- It holds: \[ \forall \, \varepsilon> 0 \,, \, \exists \, \delta >0 \, \text{ s.t. } \, \, d_Y(f(x),f(x_0))<\varepsilon\,\, \mbox{ if } \,\, d_X(x , x_0) < \delta \,. \]
Let us examine continuity in the cases of the trivial and discrete topologies.
Example 66
Let \((X,\mathcal{T}_X)\) and \((Y,\mathcal{T}_Y)\) be a topological space. Suppose that \(\mathcal{T}_Y\) is the trivial topology, that is, \[ \mathcal{T}_Y = \{ \emptyset, Y \} \,. \] Then every function \(f \colon X \to Y\) is continuous.
Indeed, we know that \(f\) is continuous if and only if it holds: \[ f^{-1}(V) \in \mathcal{T}_X \,, \quad \forall \,\, V \in \mathcal{T}_Y \,. \] We have two cases:
- \(V=\emptyset\): Then \[ f^{-1}(V) = f^{-1}(\emptyset) = \emptyset \in \mathcal{T}_X \,. \]
- \(V=Y\): Then \[ f^{-1}(V) = f^{-1}(Y) = X \in \mathcal{T}_X \,. \]
Therefore \(f\) is continuous.
Example 67
Let \((X,\mathcal{T}_X)\) and \((Y,\mathcal{T}_Y)\) be topological spaces. Suppose that \(\mathcal{T}_Y\) is the discrete topology, that is, \[ \mathcal{T}_Y = \{ V \, \text{ s.t. } \, V \subseteq Y \} \,. \] Let \(f \colon X \to Y\). They are equivalent:
- \(f\) is continuous from \(X\) to \(Y\).
- \(f^{-1}(\{y\}) \in \mathcal{T}_X\) for all \(y \in Y\).
Indeed, suppose that \(f\) is continuous. Then \[ f^{-1}(V) \in \mathcal{T}_X \,, \quad \forall \,\, V \in \mathcal{T}_Y \,. \] As \(V=\{y\} \in \mathcal{T}_Y\), we conclude that \(f^{-1}(\{y\}) \in \mathcal{T}_X\).
Conversely, assume that \(f^{-1}(\{y\}) \in \mathcal{T}_X\) for all \(y \in Y\). Let \(V \in \mathcal{T}_Y\). Trivially, we have \[ V = \bigcup_{y \in V} \, \{ y \} \,. \] Therefore \[ f^{-1}(V) = f^{-1}\left( \bigcup_{y \in V}\, \{ y \} \right) = \bigcup_{y \in V} \, f^{-1}( \{y \} ) \,. \] As \(f^{-1}( \{y \}) \in \mathcal{T}_X\) for all \(y \in Y\), by property (A2) we conclude that \(f^{-1}(V) \in \mathcal{T}_X\). Therefore \(f\) is continuous.
In a topological space, continuity preserves limits of sequences.
Proposition 68
Proof
Warning
For the above to hold, it is necessary for the topologies on \(X\) and \(Y\) to be first countable, as for example is the case for metrizable topologies, see Proposition 69 below.
Proposition 69
Proof
Example 70
Consider \(\mathbb{R}\) with the co-countable topology: \[ {\mathcal{T}}_{\textrm{cc}} := \{ A \subseteq \mathbb{R}\, \colon \,A^c = \mathbb{R}\, \mbox{ or } \, A^c \, \mbox{ countable} \} \,. \] Sequences in \((\mathbb{R},{\mathcal{T}}_{\textrm{cc}})\) converge if and only if they are eventually constant. Also consider the discrete topology on \(\mathbb{R}\), denoted by \({\mathcal{T}}_{\textrm{discrete}}\). We have seen that sequences in \((\mathbb{R},{\mathcal{T}}_{\textrm{discrete}})\) converge if and only if they are eventually constant. Consider the identity function \[ f \colon (\mathbb{R},{\mathcal{T}}_{\textrm{cc}}) \to (\mathbb{R},{\mathcal{T}}_{\textrm{discrete}}) \,, \quad f(x):=x \,. \] We have that:
\(f\) is not continuous: Indeed \(\{x\} \in {\mathcal{T}}_{\textrm{discrete}}\) but \[ f^{-1}(\{ x\}) = \{x\} \notin {\mathcal{T}}_{\textrm{cc}} \,, \] since \(\{x\}^c\) is neither \(\mathbb{R}\), nor countable.
If \(\{x_n\}\) is convergent in \({\mathcal{T}}_{\textrm{cc}}\), then it is eventually constant. Therefore \(\{f(x_n)\}\) is eventually constant, and so it is convergent in \({\mathcal{T}}_{\textrm{discrete}}\).
Let us make an observation on continuity of compositions.
Proposition 71
Proof
We conclude the section by introducing homeomorphisms.
Definition 72: Homeomoprhim
Let \((X,\mathcal{T}_X)\), \((Y,\mathcal{T}_Y)\) be topological space. A function \(f \colon X \to Y\) is called an homeomorphism if they hold:
- \(f\) is continuous.
- There exists \(g \colon Y \to X\) continuous such that \[ g \circ f = {\mathop{\mathrm{Id}}}_{X} \,, \quad f \circ g = {\mathop{\mathrm{Id}}}_{Y} \,. \]
The above is saying that \(f\) is a homeomorphism if it is continuous and has continuous inverse. Homeomorphisms are the way we say that two topological spaces look the same.
3.9 Subspace topology
Any subset \(Y\) in a topological space \(X\) inherits naturally a topological structure. Such structure is called subspace topology.
Definition 73: Subspace topology
Proof: Well-posedness of Definition 73
We have to show that \((Y,\mathcal{S})\) is a topological space:
(A1) \(\emptyset \in \mathcal{S}\) since \[ \emptyset = \emptyset \cap Y \] and \(\emptyset \in \mathcal{T}\). Similarly we have \(Y \in \mathcal{S}\), since \[ Y = X \cap Y \,, \] and \(X \in \mathcal{T}\).
(A2) Let \(A_i \in \mathcal{S}\) for \(i \in I\). By definition there exist \(U_i \in \mathcal{T}\) such that \[ A_i = U_i \cap Y \,, \quad \forall \, i \in I \,. \] Therefore \[ \bigcup_{i \in I} \, A_i = \bigcup_{i \in I} (U_i \cap Y ) = \left(\bigcup_{i \in I} U_i \right) \cap Y \,. \] The above proves that \(\cup_{i \in I} \, A_i \in \mathcal{S}\), since \(\cup_{i \in I} \, U_i \in \mathcal{T}\).
(A3) Let \(A_1, A_2 \in \mathcal{S}\). By definition there exist \(U_1,U_2 \in \mathcal{T}\) such that \[ A_1 = U_1 \cap Y \,, \quad A_2 = U_2 \cap Y \] Therefore \[ A_1 \cap A_2 = ( U_1 \cap Y ) \cap (U_2 \cap Y) = (U_1 \cap U_2) \cap Y \] The above proves that \(A_1 \cap A_2 \in \mathcal{S}\), since \(U_1 \cap U_2 \in \mathcal{T}\).
If the set \(Y\) is open, then sets are open in the subspace topology if and only if they are open in \(X\).
Proposition 74
Proof
Conversely, assume that \(A \in \mathcal{T}\). Then \[ A = A \cap Y \,, \] showing that \(A \in \mathcal{S}\).
Warning
Let \((X,\mathcal{T})\) be a topological space, \(A \subset Y \subset X\). In general we could have \[ A \in \mathcal{S}\quad \mbox{and} \quad A \notin \mathcal{T} \]
For example consider \(X=\mathbb{R}\) with \(\mathcal{T}\) the euclidean topology. Consider the subset \(Y = [0,2)\) and equip \(Y\) with the subspace topology \(\mathcal{S}\). Let \(A = [0,1)\). Then \(A \notin \mathcal{T}\) but \(A \in \mathcal{S}\), since \[ A = (-1,1) \cap Y \] and \((-1,1) \in \mathcal{T}\).
Example 75
Let \(X=\mathbb{R}\) be equipped with \(\mathcal{T}\) the euclidean topology. Let \(\mathcal{S}\) be the subspace topology on \(\mathbb{Z}\). Then \(\mathcal{S}\) coincides with the discrete topology.
Proof. The set \(\{z\}\) is open in \(\mathcal{S}\) for all \(z \in \mathbb{Z}\). Indeed, \[ \{z\} = \left( z-1 , z + 1 \right) \cap \mathbb{Z}\, \] and \((z - 1, z + 1) \in \mathcal{T}\). Thus \(\{z\} \in \mathcal{S}\). Let now \(A \subseteq \mathbb{Z}\). Then \[ A = \bigcup_{z \in A} \, \{ z \} \,, \] and therefore \(A \in \mathcal{S}\) by (A2). This proves that \[ \mathcal{S}= \{ A \, \text{ s.t. } \, A \subseteq \mathbb{Z}\} \,, \] that is, \(\mathcal{S}\) is the discrete topology on \(\mathbb{Z}\).
3.10 Topological basis
We have seen that in metric spaces every open set is union of open balls, see Propostion 27. We can then regard the open balls as building blocks for the whole topology. In this context, we call the open balls a basis for the topology.
We can generalize the concept of basis to arbitrary topological spaces.
Definition 76: Topological basis
Example 77
- Let \((X,\mathcal{T})\) be a topological space. Then \(\mathcal{B}:=\mathcal{T}\) is a basis for \(\mathcal{T}\).
This is true because one can just take \(B=U\) in (3.12).
- \((X,d)\) metric space with topology \(\mathcal{T}_d\) induced by the metric. Then \[ \mathcal{B} :=\{ B_r(x) \, \colon \,x \in X \,, \,\, r>0 \} \] is a basis for \(\mathcal{T}_d\).
This is true by Propostion 27.
- Let \((X,\mathcal{T})\) with \(X\) the discrete topology. Then \[ \mathcal{B}:=\{ \{x\} \, \colon \,x \in X \} \] is a basis for \(\mathcal{T}\).
This is true because for any \(U \in \mathcal{T}\) we have \[ U = \bigcup_{ x \in U } \, \{x\} \,. \]
Proposition 78
Let \((X,\mathcal{T})\) be a topological space and \(\mathcal{B}\) a basis for \(\mathcal{T}\). They hold:
(B1) We have \[ \bigcup_{B \in \mathcal{B}} \, B = X \,. \]
(B2) If \(U_1,U_2 \in \mathcal{B}\) then there exist \(\{B_i \} \subseteq \mathcal{B}\) such that \[ U_1 \cap U_2 = \bigcup_{i \in I} \, B_i \,. \]
Proof
(B1) This holds because \(X \in \mathcal{T}\). Therefore by definition of basis there exist \(B_i \in \mathcal{B}\) such that \[ X = \bigcup_{i \in I} \, B_i \,. \] Therefore taking the union over all \(B \in \mathcal{B}\) yields \(X\), and (B1) follows.
(B2) Let \(U_1 , U_2 \in \mathcal{B}\). Then \(U_1 , U_2 \in \mathcal{T}\), since \(\mathcal{B} \subseteq \mathcal{T}\). By property (A3) we get that \(U_1 \cap U_2 \in \mathcal{T}\). Since \(\mathcal{B}\) is a basis we conclude (B2).
Properties (B1) and (B2) from Proposition 78 are sufficient for generating a topology.
Proposition 79
Let \(X\) be a set and \(\mathcal{B}\) a collection of subsets of \(X\) such that (B1)-(B2) hold. Define \[ \mathcal{T}:= \left\{ U \subseteq X \, \colon \,U = \bigcup_{i \in I} B_i \,, \,\, B_i \in \mathcal{B} \right\} \,. \] Then:
\(\mathcal{T}\) is a topology on \(X\).
\(\mathcal{B}\) is a basis for \(\mathcal{T}\).
Proof
- We need to verify that \(\mathcal{T}\) is a topology:
(A1) We have that \(X \in \mathcal{T}\) by (B1). Moreover \(\emptyset \in \mathcal{T}\), since \(\emptyset\) can be obtained as empty union. Therefore (A1) holds.
(A2) Let \(U_i \in \mathcal{T}\) for all \(i \in I\). By definition of \(\mathcal{T}\) we have \[ U_i = \bigcup_{k \in K_i} \, B_k^i \] for some family of indices \(K_i\) and \(B_k^i \in \mathcal{B}\). Therefore \[ U := \bigcup_{i \in I} \, U_i = \bigcup_{i \in I, \, k \in K_i} \, B_k^i \,, \] showing that \(U \in \mathcal{T}\).
(A3) Suppose that \(U_1, U_2 \in \mathcal{T}\). Then \[ U_1 = \bigcup_{i \in I_1} \, B_i^1 \,, \quad U_2 = \bigcup_{i \in I_2} \, B_i^2 \] for \(B_i^1,B_i^2 \in \mathcal{B}\). From the above we have \[ U_1 \cap U_2 = \bigcup_{ i \in I_1 ,\, k \in I_2 } \, B_i^1 \cap B_k^2 \,. \] From property (B2) we have that for each pair of indices \((i,k)\) the set \(B_i^1 \cap B_k^2\) is the union of sets in \(\mathcal{B}\). Therefore \(U_1 \cap U_2\) is union of sets in \(\mathcal{B}\), showing that \(U_1 \cap U_2 \in \mathcal{T}\).
- This trivially follows from defintion of \(\mathcal{T}\) and definition of basis.
3.11 Product topology
Given two topological spaces \((X,\mathcal{T}_X)\) and \((Y,\mathcal{T}_Y)\) we would like to equip the cartesian product \[ X \times Y = \{ (x,y) \, \colon \,x \in X \,, \,\, y \in Y \} \] with a topology. We proceed as follows.
Proposition 80
The proof is an easy check, and is left as an exercise. As \(\mathcal{B}\) satisfies (B1)-(B2), by Proposition 79 we know that \[ \mathcal{T}_{X \times Y} := \left\{ U \times V \, \colon \,U \times V = \bigcup_{i \in I} B_i \,, ,\,\, B_i \in \mathcal{B} \right\} \tag{3.13}\] is a topology on \(X \times Y\).
Definition 81: Product topology
Example 82
Consider the projection maps \[ \pi_X \colon X \times Y \to X \,, \quad \pi_X (x,y):=x \] and \[ \pi_Y \colon X \times Y \to Y \,, \quad \pi_Y (x,y):=y \]
Proposition 83
Proof
The following proposition gives a useful criterion to check whether a map into \(X \times Y\) is continuous.
Proposition 84
Let \((X,\mathcal{T}_X)\) and \((Y,\mathcal{T}_Y)\) be topological spaces and equip \(X \times Y\) with the product topology \(\mathcal{T}_{X \times Y}\). Let \((Z,\mathcal{T}_Z)\) be a topological space and \[ f \colon Z \to X \times Y \] a function. They are equivalent:
- \(f\) is continuous.
- The compositions \[ \pi_X \circ f \colon Z \to X \,, \quad \pi_Y \circ f \colon Z \to Y \] are continuous.
The proof is left as an exercise.
3.12 Connectedness
Suppose that \((X,\mathcal{T})\) is a topological space. By property (A1) we have that \[ \emptyset \,, \,\, X \in \mathcal{T} \] Therefore \[ \emptyset^c = X \,, \quad X^c = \emptyset \] are closed. It follows that \(\emptyset\) and \(X\) are both open and closed.
Definition 85: Connected space
Let \((X,\mathcal{T})\) be a topological space. We say that:
- \(X\) is connected if the only subsets of \(X\) which are both open and closed are \(\emptyset\) and \(X\).
- \(X\) is disconnected if it is not connected.
The following proposition gives two extremely useful equivalent definitions of connectedness. Before stating it, we define the concept of proper set.
Definition 86: Proper subset
Proposition 87: Equivalent definition for connectedness
Let \((X,\mathcal{T})\) be a topological space. They are equivalent:
- \(X\) is disconnected.
- \(X\) is the disjoint union of two proper open subsets.
- \(X\) is the disjoint union of two proper closed subsets.
Proof
Suppose \(X\) is disconnected. Then there exists \(U \subseteq X\) which is open, closed, and such that \[ U \neq \emptyset \,, \quad U \neq X \,. \tag{3.14}\] Define \[ A:= U \,, \quad B:= U^c \,. \] By definition of complement we have \[ X = A \cup B \,, \quad A \cap B = \emptyset \,. \] Moreover:
\(A\) and \(B\) are both open and closed, since \(U\) is both open and closed.
\(A\) and \(B\) are proper, since (3.14) holds.
Therefore we conclude Points 2, 3.
Part 2. Point 2 implies Point 1. Suppose \(A,B\) are open, proper, and such that \[ X = A \cup B \,, \quad A \cap B = \emptyset \,. \] This implies \[ A^c = X \smallsetminus A = B \,, \] showing that \(A^c\) is open, and hence \(A\) is closed. Therefore \(A\) is proper, open and closed, showing that \(X\) is disconnected.
Part 3. Point 3 implies Point 1. Suppose \(A,B\) are closed, proper, and such that \[ X = A \cup B \,, \quad A \cap B = \emptyset \,. \] This implies \[ A^c = X \smallsetminus A = B \,, \] showing that \(A^c\) is closed, and hence \(A\) is open. Therefore \(A\) is proper, open and closed, showing that \(X\) is disconnected.
In the following we will use Point 2 and Point 3 in Proposition 87 as equivalent definitions of disconnected topological space.
Example 88
Consider the set \(X = \{0,1\}\) with the subspace topology induced by the inclusion \(X \subset \mathbb{R}\), where \(\mathbb{R}\) is equipped with the Euclidean topology \(\mathcal{T}_{\textrm{euclidean}}\). Then \(X\) is disconnected.
Proof. Note that \[ X = \{ 0 \} \cup \{ 1 \} \,, \quad \{ 0 \} \cap \{ 1 \} = \emptyset \,. \] The set \(\{ 0 \}\) is open for the subspace topology, since \[ \{ 0 \} = X \cap (-1,1) \,, \quad (-1,1) \in \mathcal{T}_{\textrm{euclidean}} \,. \] Similarly, also \(\{ 1 \}\) is open for the subspace topology, since \[ \{ 1 \} = X \cap (0,2) \,, \quad (0,2) \in \mathcal{T}_{\textrm{euclidean}} \,. \] Clearly \[ \{ 0 \} \neq \emptyset \,, \quad \{ 1 \} \neq \emptyset \,, \] showing that \(X\) is disconnected.
Example 89
Let \(p \in \mathbb{R}\). The set \(X = \mathbb{R}\smallsetminus \{p\}\) is disconnected.
Proof. Define the sets \[ A = (-\infty,p) \,, \quad B = (p , \infty) \,. \] Then \(A,B\) are proper subsets of \(X\), since \(p \notin X\). Moreover \[ X = A \cup B \,, \quad A \cap B = \emptyset \,. \] Finally we have that \(A,B\) are open for the subspace topology, since they are open in \(\mathbb{R}\). Therefore \(X\) is disconnected.
Example 90
Let \(n \geq 2\) and \(A \subseteq \mathbb{R}^n\) be open and connected. Let \(p \in A\). Then \(X = A \smallsetminus \{p\}\) is connected.
Exercise: Prove that \(X\) is connected.
The next theorem shows that connectedness is preserved by continuous maps.
Theorem 91
Proof
An immediate corollary of Theorem 91 is that connectedness is a topological invariant, e.g., connectedness is preserved by homeomorphisms.
Corollary 92
The proof follows immediately by Theorem 91, and is left to the reader as an exercise.
Example 93
Let \(n \geq 2\). \(\mathbb{R}^n\) not homeomorphic to \(\mathbb{R}\).
Proof. Suppose by contradiction that there exists an omeomorphism \[ f \colon \mathbb{R}^n \to \mathbb{R}\,. \] Define \(p = f(0)\) and the restriction \[ g \colon \mathbb{R}^n \smallsetminus \{0\} \to \mathbb{R}\smallsetminus \{p\} \,, \quad g(x) = f(x) \,. \] Since \(g\) is a restriction of an omeomorphism, then \(g\) is an omeomorphism. We have that \(\mathbb{R}^n \smallsetminus \{0\}\) is connected, as a consequence of
Example 90. Hence, by Corollary 92, we infer that \(\mathbb{R}\smallsetminus \{p\}\) is connected. This is a contradiction, since \(\mathbb{R}\smallsetminus \{p\}\) is disconnected, as shown in Example 89.
Example 94
Define the 1D unit circle \[ \mathbb{S}^1 := \{(x,y) \in \mathbb{R}^2 \, \colon \, x^2 + y^2 = 1 \} \,. \] Then \(\mathbb{S}^1\) and \([0,1]\) are not homeomorphic.
Proof. Suppose by contradiction that there exists and omeomorphism \[ f \colon [0,1] \to \mathbb{S}^1 \,. \] The restriction of \(f\) to \([0,1] \smallsetminus \{\frac12\}\) defines an omeomorphism \[ g \ \colon \left( [0,1] \smallsetminus \left\{\frac12\right\} \right) \to \left( \mathbb{S}^1 \smallsetminus \{\mathbf{p}\} \right) \,, \quad \mathbf{p} := f\left(\frac12 \right) \,. \] The set \([0,1] \smallsetminus \left\{ \frac12 \right\}\) is disconnected, since \[ [0,1] \smallsetminus \{1/2\} = [0,1/2) \, \cup \, (1/2,1] \] with \([0,1/2)\) and \((1/2,1]\) open for the subset topology, non-empty and disjoint. Therefore, using that \(g\) is an omeomorphism, we conclude that also \(\mathbb{S}^1 \smallsetminus \{\mathbf{p}\}\) is disconnected. Let \(\theta_0 \in [0,2\pi)\) be the unique angle such that \[ \mathbf{p} = (\cos (\theta_0),\sin(\theta_0)) \,. \] Thus \(\mathbb{S}^1 \smallsetminus \{\mathbf{p}\}\) is parametrized by \[ {\pmb{\gamma}}(t):=(\cos(t),\sin(t)) \,, \quad t \in (\theta_0,\theta_0 + 2\pi) \,. \] Since \({\pmb{\gamma}}\) is continuous and \((\theta_0,\theta_0 + 2\pi)\) is connected, by Theorem 91, we conclude that \(\mathbb{S}^1 \smallsetminus \{\mathbf{p}\}\) is connected. Contradiction.
3.13 Intermediate Value Theorem
Another consequence of Theorem 91 is a generalization of the Intermediate Value Theorem to arbitrary topological spaces. Before providing statement and proof of such Theorem, we need to characterize the connected subsets of \(\mathbb{R}\).
Definition 95: Interval
Theorem 96
Let \(\mathbb{R}\) be equipped with the Euclidean topology and let \(I \subseteq \mathbb{R}\). They are equivalent:
- \(I\) is connected.
- \(I\) is an interval.
Proof
- Since \(a<x\) and \(a \in I\), we have that \(a \in \widetilde{A}\). Therefore \(\widetilde{A} \neq \emptyset\).
- Similarly, \(b>x\) and \(b \in I\), therefore \(b \in \widetilde{B}\). Hence \(\widetilde{B} \neq \emptyset\).
Therefore \(I\) is disconnected, which is a contradiction.
Part 2. Suppose \(I\) is an interval. Suppose by contradiction that \(I\) is disconnected. Then there exist \(A,B\) proper and closed, such that \[ I = A \cup B \,, \quad A \cap B = \emptyset \,. \] Since \(A\) and \(B\) are proper, there exist points \(a \in A\), \(b \in B\). WLOG we can assume \(a<b\). Define \[ \alpha = \sup \ S \,, \quad S:= \{ x \in \mathbb{R}\colon [a,x) \cap I \subseteq A \} \,. \]
Note that \(\alpha\) exists finite since \(b\) is an upper bound for the set \(S\).
Suppose by contradiction \(b\) is not an upper bound for \(S\). Hence there exists \(x \in \mathbb{R}\) such that \([a,x) \cap I \subseteq A\) and that \(x>b\). As \(b>a\), we conclude that \(b \in [a,x) \cap I \subseteq A\). Thus \(b \in A\), which is a contradiction, since \(b \in B\) and \(A \cap B = \emptyset\).
Moreover we have that \(\alpha \in A\).
This is because the supremum \(\alpha\) is the limit of a sequence in \(S\), and hence of a sequence in \(A\). Therefore \(\alpha\) belongs to \(\overline{A}\). Since \(A\) is closed, we infer \(\alpha \in A\).
Note that \(A^c = B\), which is closed. Therefore \(A^c\) is closed, showing that \(A\) is open. As \(\alpha \in A\) and \(A\) is open in \(I\), there exists \(\varepsilon>0\) such that \[ (\alpha - \varepsilon, \alpha + \varepsilon) \cap I \subseteq A \,. \] In particular \[ [a , \alpha + \varepsilon) \cap I \subseteq A \,, \] showing that \(\alpha + \varepsilon\in S\). This is a contradiction, since \(\alpha\) is the supremum of \(S\).
We are finally ready to prove the Intermediate Value Theorem.
Theorem 97: Intermediate Value Theorem
Proof
3.14 Path connectedness
Definition 98: Path connectedness
Example 99
Let \(A \subset \mathbb{R}^n\) be convex. Then \(A\) is path connected.
A is convex if for all \(x,y \in A\) the segment connecting \(x\) to \(y\) is contained in \(A\), namely, \[ [x,y] := \{ (1-t)x + t y \, \colon \,t \in [0,1] \} \subseteq A \,. \] Therefore we can define \[ \alpha \colon [0,1] \to A \,, \quad \alpha(t):=(1-t)x + t y \,. \] Clearly \(\alpha\) is continuous, and \(\alpha(0)=x, \alpha(1)=y\).
It turns out that path-connectedness implies connectedness.
Theorem 100
Proof
The converse of the above theorem does not hold. A counterexample is given by the so-called topologist curve, which will be examined in Proposition 102. Prior to this, we need a basic Lemma.
Lemma 101
Proof
Proposition 102: Topologist curve
Proof
Let \(x \in A\) and \(y \in B\). There is no continuous function \(\alpha \colon [0,1] \to X\) such that \(\alpha(0)=x\) and \(\alpha(1)=y\). If such \(\alpha\) existed, then we would obtain a continuous extension for \(t=0\) of the function \[ f(t) = \sin \left( \frac{1}{t} \right) \,, \quad x>0 \] which is not possible. Hence \(X\) is not path connected.
Step 2. Preliminary facts.
\(A\) is connected: Define the curve \({\pmb{\gamma}}\colon (0,\infty) \to \mathbb{R}^2\) by \[ {\pmb{\gamma}}(t):= \left( t, \sin \left( \frac{1}{t} \right) \right) \,. \] Clearly \({\pmb{\gamma}}\) is continuous. Since \((0,\infty)\) is connected, by Theorem 91 we have that \({\pmb{\gamma}}((0,\infty)) = A\) is connected.
\(B\) is connected: Indeed \(B\) is homeomorphic to the interval \([-1,1]\). Since \([-1,1]\) is connected, by Corollary 92 we conclude that \(B\) is connected.
\({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} = X\): This is because each point \(y \in B\) is of the form \(y = (0,t_0)\) for some \(t_0 \in [-1,1]\). By continuity of \(\sin\) and the Intermediate Value Theorem there exists some \(z>0\) such that \[ \sin(z) = t_0 \,. \] Therefore \(z_n := z + 2n\pi\) satisfies \[ z_n \to \infty \,, \quad \sin(z_n) = t_0 \,, \quad \forall \, n \in \mathbb{N}\,. \] Define \(s_n:=1/z_n\). Trivially \[ s_n \to 0 \,, \quad \sin \left( \frac{1}{s_n} \right) = t_0 \,, \quad \forall \, n \in \mathbb{N}\,. \] Therefore we obtain \[ \left( s_n , \sin \left( \frac{1}{s_n} \right) \right) \to (0,t_0) \,. \] Hence the set \(B\) is contained in the set \(L(A)\) of limit points of \(A\). Since we are in \(\mathbb{R}^2\), we have that \(L(A)={}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\), proving that \(B \subseteq {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}\). Thus \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {}= A \cup B = X\).
Step 3. \(X\) is connected.
Let \(U \subseteq X\) be non-empty, open and closed. If we prove that \(U = X\), we conclude that \(X\) is connected. Let us proceed.
Since \(U\) is non-empty, we can fix a point \(x \in U\). We have two possibilities:
\(x \in A\): In this case \(A \cap U \neq \emptyset\). Since \(A\) is connected and \(U\) is open and closed, by Lemma 101 we conclude \(A \subseteq U\). As \(U\) is closed and contains \(A\), then \({}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} \subseteq U\). But we have shown that
\[ {}\mkern 2mu \overline{\mkern-2mu A \mkern-2mu}\mkern 2mu {} = X \,, \] and therefore \(U = X\).\(x \in B\): Then \(U \cap B \neq \emptyset\). Since \(B\) is connected and \(U\) is open and closed, we can invoke Lemma 101 and conclude that \(B \subseteq U\). Since \((0,0) \in B\), it follows that \[ (0,0) \in U \,. \] As \(U\) is open in \(X\), and \(X\) has the subspace topology induced by the inclusion \(X \subseteq \mathbb{R}^2\), there exists an open set \(W\) of \(\mathbb{R}^2\) such that \[ U = X \cap W \,. \] Therefore \((0,0) \in W\). As \(W\) is open in \(\mathbb{R}^2\), there exists a radius \(\varepsilon>0\) such that \[ B_{\varepsilon} (0,0) \subseteq W \,. \] Hence \[ X \cap B_{\varepsilon} (0,0) \subseteq X \cap W = U \,. \] The ball \(B_{\varepsilon} (0,0)\) contains points of \(A\), and therefore \[ A \cap U \neq \emptyset \,. \] Since \(A\) is connected and \(U\) is open and closed, we can again use Lemma 101 and obtain that \(A \subseteq U\). Since we already had \(B \subseteq U\), and since \(U \subseteq X = A \cup B\), we conclude hence \(U = X\).
Therefore \(U = X\) in all possible cases, showing that \(X\) is connected.