Statistical Models

Lecture 8

Dr. Silvio Fanzon

S.Fanzon@hull.ac.uk

University of Hull

Lecture 8:
The Maths of
Regression

Outline of Lecture 8

1. Simple linear regression
2. General linear regression
3. Simple regression as general regression
4. Multiple linear regression
5. Coefficient of determination R^2
6. Example of multiple regression
7. Two sample t-test as general regression

Part 1:
Simple linear
regression

Simple linear regression: Motivation

• Model: Suppose given two random variables X and Y

  • X models observed values
  • Y models a response

• Goal of Regression: Learn (approximate) the conditional distribution Y | X

  • Y | X allows to predict values of Y from values of X
  • To determine Y|X, we need the joint distribution of (X,Y)

• Problem: The joint distribution of (X,Y) is unknown. We have partial knowledge in the form of paired observations (x_1,y_1) , \ldots, (x_n,y_n) \quad \text{ observed from } \quad (X,Y)

• Goal: Use the observations (data) to learn Y|X

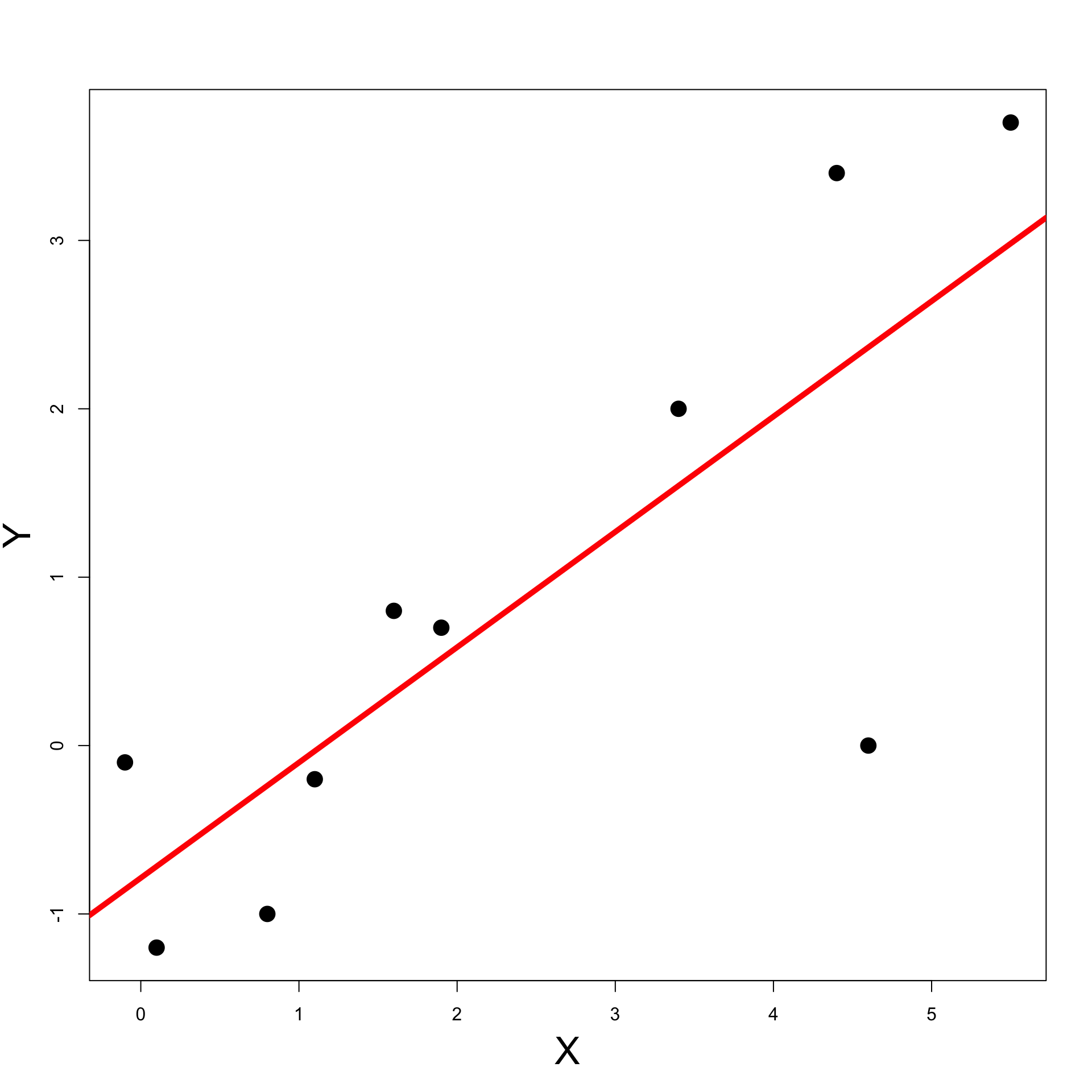
Why not just use Least-Squares?

Least-Squares:

• Naive solution to regression problem

• Find a line of best fit y = \hat \alpha + \hat \beta x

• Such line explains the data, i.e., y_i \approx \hat{y}_i \,, \qquad \hat{y}_i = \hat \alpha + \hat \beta x_i

Why not just use Least-Squares?

Drawbacks of least squares:

• Only predicts values of y such that (x,y) \, \in \, \text{ Line}

• Ignores that (x_i,y_i) come from joint distribution (X,Y)

• We don’t have meaningful estimates for the error (residuals) \varepsilon_i = y_i - \hat{y}_i \,, \qquad \hat{y}_i = \hat \alpha + \hat \beta x_i

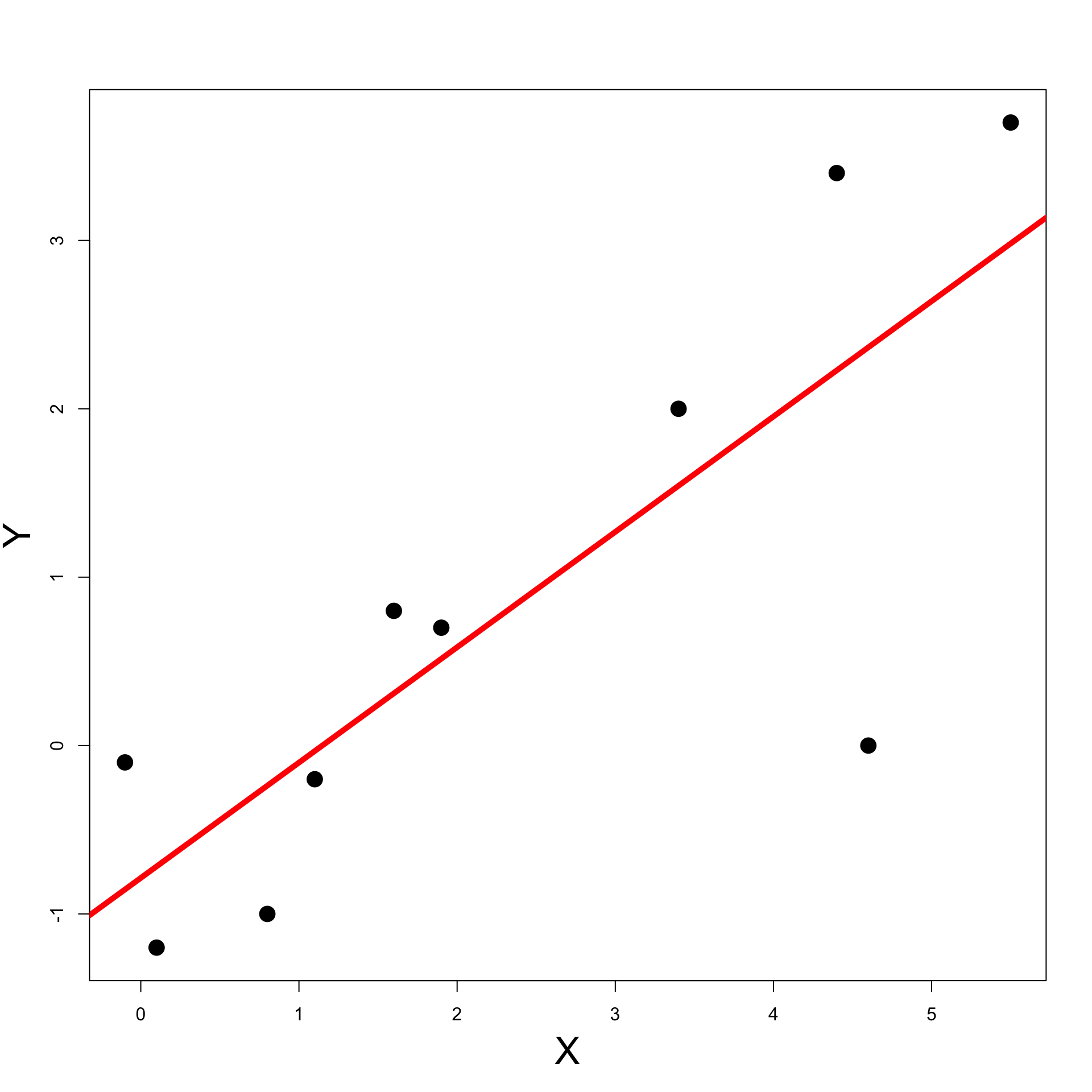
Linear Regression instead of Least Squares

Linear Regression:

• Find a regression line R(x) = \alpha + \beta x

• R(x) predicts most likely value of Y when X = x

• We will see that regression line coincides with line of best fit R(x) = \hat \alpha + \hat \beta x

• Regression gives statistical meaning to Least Squares

Regression function

Definition

Suppose given two random variables X and Y

• X is the predictor

• Y is the response

Definition

The regression function of Y on X is the conditional expectation

R \colon \mathbb{R}\to \mathbb{R}\,, \qquad \quad R(x) := {\rm I\kern-.3em E}[Y | X = x]

Regression function

Interpretation

Idea

The regression function R(x) = {\rm I\kern-.3em E}[Y | X = x] predicts the most likely value of Y when we observe X = x

Notation: We use the shorthand {\rm I\kern-.3em E}[Y|x] := {\rm I\kern-.3em E}[Y | X = x]

The regression problem

Assumption: Suppose given n observations (x_1,y_1) \,, \ldots , (x_n, y_n)

• x_i observed from X

• y_i observed from Y

Problem

From (x_1,y_1) \,, \ldots , (x_n, y_n), learn a regression function R(x) = {\rm I\kern-.3em E}[Y | x] which explains the observations, that is, such that R(x_i) = {\rm I\kern-.3em E}[Y | x_i] \ \approx \ y_i \,, \qquad \forall \, i = 1 , \ldots, n

Remember: We don’t know X and Y

Simple linear regression

• Regression problem is difficult without prior knowledge on {\rm I\kern-.3em E}[Y | x]

• A popular model is to assume that {\rm I\kern-.3em E}[Y | x] is linear

Definition

The regression function of Y on X is linear if there exist \alpha and \beta s.t. {\rm I\kern-.3em E}[Y | x] = \alpha + \beta x \,, \qquad \forall \, x \in \mathbb{R}

• \alpha and \beta are called regression coefficients

• The above regression is called simple because only 2 variables are involved

What do we mean by linear?

We said that the regression is linear if {\rm I\kern-.3em E}[Y | x ] = \alpha + \beta x Linearity in intended wrt the parameters \alpha and \beta

Examples:

• Linear regression of Y on X^2 is {\rm I\kern-.3em E}[Y | x^2 ] = \alpha + \beta x^2

• Linear regression of \log Y on 1/X is {\rm I\kern-.3em E}[ \log Y | x ] = \alpha + \beta \frac{1}{ x }

Simple linear regression

Model Assumptions

Suppose given n observations (x_1,y_1) \,, \ldots , (x_n, y_n)

• x_i observed from X

• y_i observed from Y

Definition

For each i = 1 , \ldots, n, we denote by Y_i a random variable with distribution Y | X = x_i

Model Assumptions: Recall, Y_i is distributed like Y | X = x_i

1. Predictor is known: The values x_1, \ldots, x_n are known

2. Normality: The conditional distribution Y_i is normal

3. Linear mean: There are parameters \alpha and \beta such that {\rm I\kern-.3em E}[Y_i] = \alpha + \beta x_i \,, \qquad \forall \, i = 1, \ldots, n

4. Common variance (Homoscedasticity): There is a parameter \sigma^2 such that {\rm Var}[Y_i] = \sigma^2 \,, \qquad \forall \, i = 1, \ldots, n

5. Independence: The random variables Y_1 \,, \ldots \,, Y_n are independent

Characterization of the Model

• Assumptions 1–5 look quite abstract
• The following Proposition gives a handy characterization

Proposition

Assumptions 1-5 are satisfied if and only if Y_i = \alpha + \beta x_i + \varepsilon_i for some random variables \varepsilon_1 , \ldots, \varepsilon_n \,\, \text{ iid } \,\, N(0,\sigma^2)

• The terms \varepsilon_i are called errors or residuals

Proof

• By Assumption 2, we have that Y_i is normal

• By Assumptions 3-4, we have {\rm I\kern-.3em E}[Y_i] = \alpha + \beta x_i \,, \qquad \quad {\rm Var}[Y_i] = \sigma^2

• Therefore \, Y_i \sim N(\alpha + \beta x_i, \sigma^2)

• Define the random variables \varepsilon_i by \varepsilon_i := Y_i - (\alpha + \beta x_i) \quad \qquad \left( \text{which implies } \,\, Y_i = \alpha + \beta x_i + \varepsilon_i \right)

• By Assumption 5, we have that Y_1,\ldots,Y_n are independent

• Therefore \varepsilon_1,\ldots, \varepsilon_n are independent

• Since Y_i \sim N(\alpha + \beta x_i, \sigma^2), we conclude that \varepsilon_i are iid N(0,\sigma^2)

• Therefore, Y_i = \alpha + \beta x_i + \varepsilon_i with \varepsilon_i iid N(0,\sigma^2) \qquad \qquad \qquad \qquad \quad \qquad \square

Likelihood function

Let X_1, \ldots, X_n be continuous rv with joint pdf f = f(x_1, \ldots, x_n | \theta) \,, \qquad \theta \in \Theta \,\, \, \text{ parameter}

Definition

The likelihood function of (X_1, \ldots, X_n) for a given sample (x_1, \ldots, x_n) is L \colon \Theta \to \mathbb{R}\,, \qquad \quad L(\theta | x_1,\ldots, x_n ) := f(x_1, \ldots, x_n | \theta)

Theorem

Suppose Assumptions 1–5 hold. The likelihood function of (Y_1,\ldots,Y_n) is

L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \Bigg( -\frac{\sum_{i=1}^n(y_i-\alpha - \beta x_i)^2}{2\sigma^2} \Bigg)

Proof

• By the Assumptions, we have Y_i \sim N( \alpha + \beta x_i , \sigma^2 )

• Therefore, the pdf of Y_i is f_{Y_i} (y_i) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp \Bigg( -\frac{(y_i-\alpha-\beta{x_i})^2}{2\sigma^2} \Bigg)

• Since Y_1,\ldots, Y_n are independent, we obtain \begin{align*} L(\alpha,\beta, \sigma^2 | y_1, \ldots,y_n) & = f(y_1,\ldots,y_n) = \prod_{i=1}^n f_{Y_i}(y_i) \\ & = \prod_{i=1}^n \frac{1}{\sqrt{2\pi \sigma^2}} \exp \Bigg( -\frac{(y_i-\alpha-\beta{x_i})^2}{2\sigma^2} \Bigg) \\ & = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \Bigg( -\frac{\sum_{i=1}^n(y_i- \alpha - \beta x_i)^2}{2\sigma^2} \Bigg) \qquad \qquad \square \end{align*}

Model Summary

• Simple linear regression of Y on X is the function {\rm I\kern-.3em E}[Y | x] = \alpha + \beta x

• Suppose given n observations (x_1,y_1) \,, \ldots , (x_n, y_n)

  • x_i observed from X
  • y_i observed from Y

• Denote by Y_i the random variable Y | X = x_i

• We suppose that Y_i has the form Y_i = \alpha + \beta x_i + \varepsilon_i \,, \qquad \varepsilon_i \, \text{ iid } \, N(0,\sigma^2)

• In particular {\rm I\kern-.3em E}[Y|x_i] = {\rm I\kern-.3em E}[Y_i] = \alpha + \beta x_i

The linear regression problem

Problem

Given observations (x_1,y_1) \,, \ldots , (x_n, y_n), learn a linear regression function {\rm I\kern-.3em E}[Y | x] = \alpha + \beta x which explains the observations, that is, such that \begin{equation} \tag{1} {\rm I\kern-.3em E}[Y_i] = {\rm I\kern-.3em E}[Y | x_i] \ \approx \ y_i \,, \qquad \forall \, i = 1 , \ldots, n \end{equation}

Question

How do we enforce (1)?

Answer: Recall condition (1) from previous slide \begin{equation} \tag{1} {\rm I\kern-.3em E}[Y_i] \ \approx \ y_i \,, \qquad \forall \, i = 1 , \ldots, n \end{equation}

• If we want (1) to hold, we need to maximize the joint probability \begin{equation}\tag{P} P(Y_1 \approx y_1, \ldots, Y_n \approx y_n) = \int_{A} f(y) \, dy \approx |A| f(y) \end{equation}

  • where f is the joint pdf of (Y_1,\ldots, Y_n)
  • A is (small) open set in \mathbb{R}^n containing the observations (y_1,\ldots,y_n)
  • |A| is the n-dimensional volume of A

• To maximize the probability, by (P), it is enough to maximize f(y_1,\ldots,y_n)

• Therefore, choose parameters \hat \alpha, \hat \beta, \hat \sigma which maximize the likelihood function \max_{\alpha,\beta,\sigma} f(y_1,\ldots,y_n | \alpha,\beta, \sigma^2) = \max_{\alpha,\beta,\sigma} \ L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) Maximum Likelihood Estimation: Find parameters that maximize the Likelihood, and so (P)

Maximum Likelihood Estimation

Theorem

Suppose Assumptions 1–5 hold. Assume given n observations (x_1,y_1), \ldots, (x_n,y_n). The maximization problem \max_{\alpha,\beta,\sigma} \ L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) admits the unique solution \hat \alpha = \overline{y} - \hat \beta \, \overline{x} \,, \qquad \hat \beta = \frac{S_{xy}}{S_{xx}} \,, \qquad \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n \left( y_i - \hat \alpha - \hat \beta x_i \right)^2

• The constants \hat \alpha, \hat \beta, \hat{\sigma}^2 are called Maximum Likelihood Estimators (MLE)

• Important: \hat \alpha and \hat \beta are the Least Squares coefficients!

Proof of Theorem

• The \log function is strictly increasing. Therefore \max_{\alpha,\beta,\sigma} \ L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) \quad \text{ is equivalent to } \quad \max_{\alpha,\beta,\sigma} \ \log L( \alpha,\beta, \sigma^2 | y_1, \ldots, y_n )

• Recall that the likelihood is L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \left( - \frac{\sum_{i=1}^n(y_i-\alpha - \beta x_i)^2}{2\sigma^2} \right)

• Hence the log–likelihood is \log L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) = - \frac{n}{2} \log (2 \pi) - \frac{n}{2} \log \sigma^2 - \frac{ \sum_{i=1}^n(y_i-\alpha - \beta x_i)^2 }{2 \sigma^2}

• Suppose first that \sigma is fixed. In this case the problem \max_{\alpha,\beta} \ \left\{ \frac{n}{2} \log (2 \pi) - \frac{n}{2} \log \sigma^2 - \frac{ \sum_{i=1}^n(y_i-\alpha - \beta x_i)^2 }{2 \sigma^2} \right\} is equivalent to \min_{\alpha, \beta} \ \sum_{i=1}^n(y_i-\alpha - \beta x_i)^2

• This is the Least Squares problem! Hence the solution is \hat \alpha = \overline{y} - \hat \beta \, \overline{x} \,, \qquad \hat \beta = \frac{S_{xy}}{S_{xx}}

• Substituting \hat \alpha and \hat \beta we obtain \begin{align*} \max_{\alpha,\beta,\sigma} \ & \log L(\alpha,\beta, \sigma^2 | y_1, \ldots, y_n ) = \max_{\sigma} \ \log L(\hat \alpha, \hat \beta, \sigma^2 | y_1, \ldots, y_n ) \\[10pt] & = \max_{\sigma} \ \left\{ - \frac{n}{2} \log (2 \pi) - \frac{n}{2} \log \sigma^2 - \frac{ \sum_{i=1}^n(y_i-\hat\alpha - \hat\beta x_i)^2 }{2 \sigma^2} \right\} \end{align*}

• The above is a one-dimensional minimization problem in \sigma

• Taking the first order derivative wrt \sigma, it can be shown the unique solution is \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n \left( y_i - \hat \alpha - \hat \beta x_i \right)^2

• This concludes the proof

Least-squares vs Linear regression

Linear regression and least-squares give seemingly the same answer

Least-squares line	y = \hat \alpha + \hat \beta x
Linear regression line	{\rm I\kern-.3em E}[Y | x ] = \hat \alpha + \hat \beta x

Question: Why did we define regression if it gives same answer as least-squares?

Answer: There is actually a big difference

• Least-squares line y = \hat \alpha + \hat \beta x is just a geometric object
  • We don’t have meaningful estimates for the error (residuals) \varepsilon_i = y_i - \hat{y_i} \,, \qquad \hat{y}_i = \hat \alpha + \hat \beta_n
• Regression line {\rm I\kern-.3em E}[Y | x ] = \hat \alpha + \hat \beta x is Statistical model for Y|X
  • Can quantify in probability how well the linear model fits the data

Part 2:
General linear
regression

Simple vs General regression

Simple regression: Response variable Y depends on one predictor X

• The goal is to learn the distribution of

  Y | X

• Y | X allows to predict values of Y, knowing values of X

General regression: Response variable Y depends on p predictors Z_1 , \ldots, Z_p

• The goal is to learn the distribution of Y | Z_1, \ldots, Z_p

• Y | Z_1 , \dots, Z_p allows to predict values of Y, knowing values of Z_1 , \dots, Z_p

General regression function

Suppose given random variables Z_1 , \ldots, Z_p and Y

• Z_1,\ldots, Z_p are the predictors

• Y is the response

Notation: We denote points of \mathbb{R}^p by z = (z_1, \ldots, z_p)

Definition

The regression function of Y on Z_1,\ldots,Z_p is the conditional expectation

R \colon \mathbb{R}^p \to \mathbb{R}\,, \qquad \quad R(z) := {\rm I\kern-.3em E}[Y | Z_1 = z_1, \ldots , Z_p = z_p]

General regression function

Idea

The regression function R(z) = {\rm I\kern-.3em E}[Y | Z_1 = z_1, \ldots , Z_p = z_p] predicts the most likely value of Y when we observe Z_1 = z_1, \,\,\ldots , \,\, Z_p = z_p

Notation: We use the shorthand {\rm I\kern-.3em E}[Y | z_1, \ldots, z_p] := {\rm I\kern-.3em E}[Y | Z_1 = z_1, \ldots , Z_p = z_p]

The general regression problem

Assumption: For each i =1 , \ldots, n we assume given observations

• data point (z_{i1}, \ldots, z_{ip}, y_i)

• z_{ij} is from Z_j

• y_i is from Y

Problem

From the above data, learn a regression function R(z) = {\rm I\kern-.3em E}[Y | z_1, \ldots, z_p] which explains the observations, that is, such that {\rm I\kern-.3em E}[Y | z_{i1}, \ldots, z_{ip}] \ \approx \ y_i \,, \qquad \forall \, i = 1 , \ldots, n

General linear regression

Key assumption: The regression function R(z) = {\rm I\kern-.3em E}[Y | z_1, \ldots, z_p] is linear

Definition

The regression of Y on Z_1 , \ldots, Z_p is linear if there exist \beta_1, \ldots, \beta_p s.t.

{\rm I\kern-.3em E}[Y | z_1, \ldots, z_p] = \beta_1 z_1 + \ldots + \beta_p z_p \,, \quad \forall \, z \in \mathbb{R}^p

\beta_1, \ldots, \beta_p are called regression coefficients

Note:

• In simple regression we have 2 coefficients \alpha and \beta

• In multiple regression we have p coefficients \beta_1, \ldots, \beta_p

General linear regression

Model Assumptions

For each i =1 , \ldots, n we assume given

• data point (z_{i1}, \ldots, z_{ip}, y_i)

• z_{ij} is from Z_j

• y_i is from Y

Definition

For each i = 1, \ldots, n, we denote by Y_i a random variable with distribution Y | Z_1 = z_{i1} , \ldots, Z_p = z_{ip}

Model Assumptions: Recall, Y_i is distributed like Y | Z_1 = z_{i1} , \ldots, Z_p = z_{ip}

1. Predictor is known: The values z_{i1}, \ldots, z_{ip} are known

2. Normality: The conditional distribution Y_i is normal

3. Linear mean: There are parameters \beta_1,\ldots,\beta_p such that {\rm I\kern-.3em E}[Y_i] = \beta_1 z_{i1} + \ldots + \beta_p z_{ip} \,, \qquad \forall \, i = 1, \ldots, n

4. Common variance (Homoscedasticity): There is a parameter \sigma^2 such that {\rm Var}[Y_i] = \sigma^2 \,, \qquad \forall \, i = 1, \ldots, n

5. Independence: The random variables Y_1 \,, \ldots \,, Y_n are independent

Characterization of the Model

• Assumptions 1–5 look quite abstract
• The following Proposition gives a handy characterization

Proposition

Assumptions 1-5 are satisfied if and only if Y_i = \beta_1 z_{i1} + \ldots + \beta_p z_{ip} + \varepsilon_{i} for some errors or residuals \varepsilon_1 , \ldots, \varepsilon_n \,\, \text{ iid } \,\, N(0,\sigma^2)

Proof: Similar to the proof of Proposition in Slide 14. Omitted

Likelihood function

Introduce the column vectors \beta := (\beta_1, \ldots, \beta_p)^T \,, \qquad y := (y_1,\ldots,y_n)^T

Theorem

Suppose Assumptions 1–5 hold. The likelihood function of (Y_1,\ldots,Y_n) is L(\beta, \sigma^2 | y ) = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \left( -\frac{\sum_{i=1}^n(y_i- \beta_1 z_{i1} - \ldots - \beta_p z_{ip})^2}{2\sigma^2} \right)

Proof

• By the Assumptions, we have Y_i \sim N(\beta_1 z_{i1} + \ldots + \beta_p z_{ip} , \sigma^2 )

• Therefore, the pdf of Y_i is f_{Y_i} (y_i) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp \left( -\frac{(y_i - \beta_1 z_{i1} - \ldots - \beta_p z_{ip})^2}{2\sigma^2} \right)

• Since Y_1,\ldots, Y_n are independent, we obtain \begin{align*} L(\beta, \sigma^2 | y) & = f(y_1,\ldots,y_n) = \prod_{i=1}^n f_{Y_i}(y_i) \\ & = \prod_{i=1}^n \frac{1}{\sqrt{2\pi \sigma^2}} \exp \left( -\frac{(y_i - \beta_1 z_{i1} - \ldots - \beta_p z_{ip})^2}{2\sigma^2} \right) \\ & = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \left( -\frac{\sum_{i=1}^n(y_i- \beta_1 z_{i1} - \ldots - \beta_p z_{ip})^2}{2\sigma^2} \right) \qquad \quad \square \end{align*}

Design matrix

For each i = 1 , \ldots, n suppose given p observations z_{i1}, \ldots, z_{ip}

Definition

The design matrix is the n \times p matrix Z := \left( \begin{array}{ccc} z_{11} & \ldots & z_{1p} \\ z_{21} & \ldots & z_{2p} \\ \ldots & \ldots & \ldots \\ z_{n1} & \ldots & z_{np} \\ \end{array} \right)

Vectorial notation

\begin{align*} y - Z\beta & = \left( \begin{array}{c} y_1 \\ y_2 \\ \ldots \\ y_n \\ \end{array} \right) - \left( \begin{array}{ccc} z_{11} & \ldots & z_{1p} \\ z_{21} & \ldots & z_{2p} \\ \ldots & \ldots & \ldots \\ z_{n1} & \ldots & z_{np} \\ \end{array} \right) \left( \begin{array}{c} \beta_1 \\ \ldots \\ \beta_p \\ \end{array} \right) \\[20pt] & = \left( \begin{array}{c} y_1 \\ y_2 \\ \ldots \\ y_n \\ \end{array} \right) - \left( \begin{array}{c} \beta_1 z_{11} + \ldots + \beta_p z_{1p}\\ \beta_1 z_{21} + \ldots + \beta_p z_{2p} \\ \ldots \\ \beta_1 z_{n1} + \ldots + \beta_p z_{np} \\ \end{array} \right) \\[20pt] & = \left( \begin{array}{c} y_1 - \beta_1 z_{11} - \ldots - \beta_p z_{1p}\\ y_2 - \beta_1 z_{21} - \ldots - \beta_p z_{2p} \\ \ldots \\ y_n - \beta_1 z_{n1} - \ldots - \beta_p z_{np} \\ \end{array} \right) \, \in \, \mathbb{R}^n \end{align*}

RSS: Residual Sum of Squares

From the previous calculation, we get

(y - Z \beta)^T \, (y - Z\beta) = \sum_{i=1}^n \left( y_i - \beta_1 z_{i1} - \ldots - \beta_p z_{ip} \right)^2

Definition

Assume given

• n \times p design matrix Z

• vector y \in \mathbb{R}^n

The residual sum of squares associated to the parameter \beta is the function \mathop{\mathrm{RSS}}\colon \mathbb{R}^p \to \mathbb{R}\,, \qquad \mathop{\mathrm{RSS}}(\beta) := (y - Z \beta)^T \, (y - Z\beta)

Likelihood function

Vectorial notation

Using vectorial notation, the likelihood function can be re-written as

\begin{align*} L(\beta, \sigma^2 | y ) & = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \left( -\frac{\sum_{i=1}^n(y_i - \beta_1 z_{i1} - \ldots - \beta_p z_{ip})^2}{2\sigma^2} \right) \\[20pt] & = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \left( - \frac{ (y - Z \beta)^T \, (y - Z\beta) }{2 \sigma^2} \right) \\[20pt] & = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \left( - \frac{\mathop{\mathrm{RSS}}(\beta) }{2 \sigma^2} \right) \end{align*}

Model Summary

• General linear regression of Y on Z_1, \ldots, Z_p is the function {\rm I\kern-.3em E}[Y | z_1,\ldots,z_p] = \beta_1 z_{1} + \ldots + \beta_p z_p

• For each i=1, \ldots, n suppose given the observations

  • (z_{i1}, \ldots, z_{ip}, y_i) observed from (Z_1,\ldots, Z_p,Y)

• Denote by Y_i the random variable Y | z_{i1} ,\ldots, z_{ip}

• We suppose that Y_i has the form Y_i = \beta_1 z_{i1} + \ldots + \beta_p z_{ip} + \varepsilon_i \,, \qquad \varepsilon_i \,\, \text{ iid } \,\, N(0,\sigma^2)

• In particular, {\rm I\kern-.3em E}[Y | z_{i1}, \ldots, z_{ip}] = {\rm I\kern-.3em E}[Y_i] = \beta_1 z_{i1} + \ldots + \beta_p z_{ip}

The general linear regression problem

For each i = 1 , \ldots, n suppose given data points (z_{i1}, \ldots, z_{ip}, y_i)

Problem

From the above data, learn a general linear regression function {\rm I\kern-.3em E}[Y | z_1, \ldots, z_p] = \beta_1 z_1 + \ldots + \beta_p z_p which explains the observations, that is, such that \begin{equation} \tag{2} {\rm I\kern-.3em E}[Y_i] = {\rm I\kern-.3em E}[Y | z_{i1}, \ldots, z_{ip}] \ \approx \ y_i \,, \qquad \forall \, i = 1 , \ldots, n \end{equation}

Question

How do we enforce (2)?

Answer: Recall condition (2) from the previous slide \begin{equation} \tag{2} {\rm I\kern-.3em E}[Y_i] \ \approx \ y_i \,, \qquad \forall \, i = 1 , \ldots, n \end{equation}

• If we want (2) to hold, we need to maximize the joint probability \begin{equation}\tag{P} P(Y_1 \approx y_1, \ldots, Y_n \approx y_n) = \int_{A} f(y) \, dy \approx |A| f(y) \end{equation}

  • where f is the joint pdf of (Y_1,\ldots,Y_n)
  • A is a (small) open set in \mathbb{R}^n containing the observations (y_1,\ldots,y_n)
  • |A| is the n-dimensional volume of A

• To maximize the probability, by (P), it is enough to maximize f(y_1,\ldots,y_n)

• Therefore, choose parameters \hat \beta, \hat \sigma which maximize the likelihood function \max_{\beta,\sigma} \ f(y | \beta, \sigma^2) = \max_{\beta,\sigma} \ L(\beta, \sigma^2 | y )

Maximum Likelihood Estimation

Theorem

Suppose Assumptions 1–5 hold. Assume given observations (z_{i1}, \ldots, z_{ip} ,y_i) \,, \quad \forall \, i =1 ,\ldots n \,, \qquad \text{ s.t. } \,\, \det (Z Z^T) \neq 0 The maximization problem \max_{\beta,\sigma} \ L(\beta, \sigma^2 | y ) admits the unique solution \hat \beta = (Z^T Z)^{-1} Z^T y \,, \qquad \hat{\sigma}^2 = \frac{1}{n} \mathop{\mathrm{RSS}}(\hat \beta)

• The constants \hat \beta, \hat{\sigma}^2 are called Maximum Likelihood Estimators (MLE)

Minimizing the RSS

The proof of previous Theorem relies on the following Lemma

Lemma

Assume given observations (z_{i1}, \ldots, z_{ip} ,y_i) \,, \quad \forall \, i =1 ,\ldots n \,, \qquad \text{ s.t. } \,\, \det (Z Z^T) \neq 0 The minimization problem \min_{\beta} \ \mathop{\mathrm{RSS}}(\beta) admits the unique solution \hat \beta = (Z^T Z)^{-1} Z^T y

Results from matrix calculus

• To prove the Lemma we need some auxiliary results

• In the following, x denotes an n \times 1 column vector

x = \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right)

Results from matrix calculus

First result

• Suppose given an n \times 1 column vector a

• Define the scalar function

f \colon \mathbb{R}^n \to \mathbb{R}\,, \qquad f(x) := a^T x

• Then f is differentiable and the gradient is constant

\nabla f (x) = a^T

Results from matrix calculus

Second result

• Suppose given an m \times n matrix A

• Define the vectorial affine function

g \colon \mathbb{R}^n \to \mathbb{R}^m \,, \qquad g(x) := A x

• Then g is differentiable and the Jacobian is constant

J g (x) = A

Results from matrix calculus

Third result

• Suppose given an n \times n matrix M

• Define the quadratic form

h \colon \mathbb{R}^n \to \mathbb{R}\,, \qquad h(x) := x^T M x

• Then h is differentiable and the Jacobian is

J h(x) = x^T (M + M^T)

Additional results on the matrix transpose

1. For any m \times n matrix A (A^T)^T= A

2. A square matrix M of size n \times n is symmetric iff M^T = M

3. Scalars can be seen as 1 \times 1 symmetric matrices. Therefore c^T = c \,, \qquad \forall \, c \in \mathbb{R}

4. For any m \times n matrix A and n \times p matrix B (AB)^T=B^T A^T

5. The matrix A^T A is symmetric by point (2) (A^T A)^T = A^T (A^T)^T = A^T A

Optimality conditions

We also need the n-dimensional version of the Lemma in Slide 103 Lecture 7

Lemma

Suppose f \colon \mathbb{R}^n \to \mathbb{R} has positive semi-definite Hessian. They are equivalent

1. The point \hat x is a minimizer of f, that is, such that

f( \hat x ) = \min_{x \in \mathbb{R}^n} f(x)

2. The point \hat x satisfies the optimality conditions

\nabla f (\hat x) = 0

Proof: Minimizing the RSS

• Recall the definition of Residual Sum of Squares \mathop{\mathrm{RSS}}\colon \mathbb{R}^{p} \to \mathbb{R}\,, \qquad \mathop{\mathrm{RSS}}(\beta) = (y - Z \beta)^T (y - Z \beta)

• We are finally ready to minimize the \mathop{\mathrm{RSS}} \min_{\beta \in \mathbb{R}^p} \ \mathop{\mathrm{RSS}}(\beta)

• It is not too difficult to show that \nabla^2 \mathop{\mathrm{RSS}} is positive-semidefinite (omitted)

• By the Lemma on Optimality Conditions in Slide 50 \beta \,\, \text{ minimizes } \,\, \mathop{\mathrm{RSS}}\qquad \iff \qquad \nabla \mathop{\mathrm{RSS}}(\beta) = 0

• To compute \nabla \mathop{\mathrm{RSS}}, we first expand \mathop{\mathrm{RSS}} \begin{align*} \mathop{\mathrm{RSS}}(\beta) & = (y-Z \beta)^T (y-Z \beta) \\[5pt] & = (y^T - (Z\beta)^T ) (y-Z \beta) \\[5pt] & = (y^T - \beta^T Z^T ) (y-Z \beta) \\[5pt] & = y^T y - y^T Z \beta - \beta^T Z^T y + \beta^T Z^T Z \beta \end{align*}

• Note that

  • \beta has size p \times 1 \quad \implies \quad \beta^T has size 1 \times p
  • Z has size n \times p \quad \implies \quad Z^T has size p \times n
  • y has size n \times 1 \quad \implies \quad \beta^T Z^T y has size \left( 1 \times p \right) \times \left( p \times n \right) \times \left( n \times 1 \right) = 1 \times 1

• \beta^T Z^T y \, is a scalar \quad \implies \quad it is symmetric and we get \left( \beta^T Z^T y \right)^T = \beta^T Z^T y

• Using the properties of transposition we also get \left( \beta^T Z^T y \right)^T = y^T Z \beta

• From the last 2 equations we conclude \beta^T Z^T y = y^T Z \beta

• The \mathop{\mathrm{RSS}} can now be written as \begin{align*} \mathop{\mathrm{RSS}}(\beta) & = y^T y - y^T Z \beta - \textcolor{magenta}{\beta^T Z^T y} + \beta^T Z^T Z \beta \\[5pt] & = y^T y - y^T Z \beta - \textcolor{magenta}{y^T Z \beta} + \beta^T Z^T Z \beta \\[5pt] & = y^T y - 2 y^T Z \beta + \beta^T Z^T Z \beta \end{align*}

• Therefore, we have \begin{align*} \nabla \mathop{\mathrm{RSS}}(\beta) & = \nabla ( y^T y ) - 2 \nabla (y^T Z \beta ) + \nabla (\beta^T Z^T Z \beta ) \\[5pt] & = - 2 \nabla (y^T Z \beta ) + \nabla (\beta^T Z^T Z \beta ) \end{align*}

• We need to compute \nabla (y^T Z \beta ) \qquad \quad \text{ and } \qquad \quad \nabla (\beta^T Z^T Z \beta )

• Note that y^T Z has dimension \, ( 1 \times n ) \times ( n \times p ) = 1 \times p

• Since \beta has dimension p \times 1, we can define the function f \colon \mathbb{R}^p \to \mathbb{R}\,, \qquad f(\beta) := y^T Z \beta

• By the First Result on Matrix Calculus in Slide 46 \nabla f = \nabla ( \textcolor{magenta}{y^T Z} \beta) = \textcolor{magenta}{y^T Z}

• Note that Z^T Z has dimension \, ( p \times n ) \times ( n \times p ) = p \times p

• Since \beta has dimension p \times 1, we can define the function

h \colon \mathbb{R}^p \to \mathbb{R}\,, \qquad h(\beta) := \beta^T Z^T Z \beta

• By the Third Result on Matrix Calculus in Slide 48 \begin{align*} \nabla h & = \nabla (\beta^T \textcolor{magenta}{Z^T Z} \beta) = \beta^T (\textcolor{magenta}{Z^T Z} + (\textcolor{magenta}{Z^T Z})^T ) \\[5pt] & = \beta^T ( Z^T Z + Z^T Z ) = 2 \beta^T (Z^T Z) \end{align*}

• Putting together these results we obtain

\begin{align*} \nabla \mathop{\mathrm{RSS}}(\beta) & = - 2 \nabla (y^T Z \beta ) + \nabla (\beta^T Z^T Z \beta ) \\[5pt] & = -2 y^T Z + 2 \beta^T (Z^T Z) \end{align*}

• We can finally solve the optimality conditions: \begin{align*} \nabla \mathop{\mathrm{RSS}}(\beta) = 0 \qquad & \iff \qquad -2 y^T Z + 2 \beta^T (Z^T Z) = 0 \\[5pt] & \iff \qquad \beta^T (Z^T Z) = y^T Z \end{align*}

• Transposing both sides of the last equation yields \begin{equation} \tag{3} (Z^T Z) \beta = Z^T y \end{equation}

• The matrix Z^T Z is invertible, since we are assuming \det (Z^T Z) \neq 0

• Multiplying by (Z^T Z)^{-1} both sides of (3), we get \beta = (Z^T Z)^{-1} Z^T y

• In conclusion, we have shown that

\nabla \mathop{\mathrm{RSS}}(\beta) = 0 \qquad \iff \qquad \beta = (Z^T Z)^{-1} Z^T y

• By the Lemma on Optimality Conditions in Slide 50, we infer

\beta = (Z^T Z)^{-1} Z^T y \,\,\, \text{ minimizes } \,\,\, \mathop{\mathrm{RSS}}

• This concludes the proof

Maximum Likelihood Estimation

We are finally in position to prove the main Theorem. We recall the statement

Theorem

Suppose Assumptions 1–5 hold. Assume given observations (z_{i1}, \ldots, z_{ip} ,y_i) \,, \quad \forall \, i =1 ,\ldots n \,, \qquad \text{ s.t. } \,\, \det (Z Z^T) \neq 0 The maximization problem \max_{\beta,\sigma} \ L(\beta, \sigma^2 | y ) admits the unique solution \hat \beta = (Z^T Z)^{-1} Z^T y \,, \qquad \hat{\sigma}^2 = \frac{1}{n} \mathop{\mathrm{RSS}}(\hat \beta)

Proof of Theorem

• The \log function is strictly increasing. Therefore \max_{\beta,\sigma} \ L(\beta, \sigma^2 | y ) \quad \text{ is equivalent to } \quad \max_{\beta,\sigma} \ \log L( \beta, \sigma^2 | y )

• Recall that the likelihood is L(\beta, \sigma^2 | y ) = \frac{1}{(2\pi \sigma^2)^{n/2}} \, \exp \left( - \frac{ \mathop{\mathrm{RSS}}(\beta) }{2\sigma^2} \right)

• Hence, the log–likelihood is \log L(\beta, \sigma^2 | y ) = - \frac{n}{2} \log (2 \pi) - \frac{n}{2} \log \sigma^2 - \frac{ \mathop{\mathrm{RSS}}(\beta) }{2 \sigma^2}

• Suppose first that \sigma is fixed. In this case the problem \max_{\beta} \ \left\{ \frac{n}{2} \log (2 \pi) - \frac{n}{2} \log \sigma^2 - \frac{ \mathop{\mathrm{RSS}}(\beta) }{2 \sigma^2} \right\} is equivalent to \min_{\beta} \ \mathop{\mathrm{RSS}}(\beta)

• We have already proven that the \mathop{\mathrm{RSS}} is minimized at \hat \beta = (Z^T Z)^{-1} Z^T y

• Substituting \hat \beta, we obtain

\begin{align*} \max_{\beta,\sigma} \ & \log L(\beta, \sigma^2 | y ) = \max_{\sigma} \ \log L(\hat \beta, \sigma^2 | y ) \\[5pt] & = \max_{\sigma} \ \left\{ - \frac{n}{2} \log (2 \pi) - \frac{n}{2} \log \sigma^2 - \frac{ \mathop{\mathrm{RSS}}(\hat \beta) }{2 \sigma^2} \right\} \end{align*}

• The above is a one-dimensional minimization problem in \sigma

• Taking the first order derivative wrt \sigma, it can be shown the unique solution is \hat{\sigma}^2 = \frac{1}{n} \mathop{\mathrm{RSS}}(\hat \beta)

• This concludes the proof

Part 3:
Simple regression as
general regression

General linear regression model

• The general linear regression model is

Y_i = \beta_1 z_{i1} + \ldots + \beta_p z_{ip} + \varepsilon_i \,, \quad \varepsilon_i \sim N(0,\sigma^2) \quad \, \forall \, i = 1 , \ldots, n

• The design matrix, and data and parameters vectors are Z = \left( \begin{array}{ccc} z_{11} & \ldots & z_{1p} \\ \ldots & \ldots & \ldots \\ z_{n1} & \ldots & z_{np} \\ \end{array} \right) \in \mathbb{R}^{n \times p} \,, \qquad y = \left( \begin{array}{c} y_1 \\ \ldots \\ y_{n} \\ \end{array} \right)\,, \qquad \beta = \left( \begin{array}{c} \beta_1 \\ \ldots \\ \beta_{p} \\ \end{array} \right)

• The likelihood function for general linear regression is maximized by \hat \beta = (Z^T Z)^{-1} Z^T y

Simple linear regression model

• The simple linear regression model is

Y_i = \alpha + \beta x_i + \varepsilon_i \,, \,, \quad \varepsilon_i \sim N(0,\sigma^2) \quad \, \forall \, i = 1 , \ldots, n

• The data is given by x = \left( \begin{array}{c} x_1 \\ \ldots \\ x_{n} \\ \end{array} \right) \qquad \quad y = \left( \begin{array}{c} y_1 \\ \ldots \\ y_{n} \\ \end{array} \right)

• The likelihood function for simple linear regression is maximized by \hat \alpha = \overline{y} - \hat \beta \, \overline{x} \,, \qquad \quad \hat \beta = \frac{S_{xy}}{S_{xx}}

Simple linear regression from general

• The general regression model comprises the simple regression one

• To see this, consider a general linear model with p = 2 parameters

Y_i = \beta_1 z_{i1} + \beta_2 z_{i2} + \varepsilon_i \,, \qquad i = 1 , \ldots, n

• We want to compare the above to

Y_i = \alpha + \beta x_i + \varepsilon_i \,, \qquad i = 1 , \ldots, n

• The 2 models are equivalent iff

z_{i1} = 1 \,, \qquad z_{i2} = x_i \,, \qquad \forall \, i = 1 , \ldots, n

Therefore, the design matrix is Z = \left( \begin{array}{cc} 1 & x_{1} \\ \ldots & \ldots \\ 1 & x_{n} \\ \end{array} \right) \in \mathbb{R}^{n \times 2}

Theorem

With the above definition of Z, it holds that (Z^T Z)^{-1} Z^T y = \left( \begin{array}{cc} \hat \alpha \\ \hat \beta \end{array} \right) \,, \qquad \hat \alpha = \overline{y} - \hat \beta \overline{x} \,, \qquad \hat \beta = \frac{S_{xy}}{S_{xx}}

In other words, the multiple linear regression estimator (Z^T Z)^{-1} Z^T y coincides with the simple linear regression estimators \hat \alpha, \hat \beta

Proof: Calculating Z^T y

• Z has size n \times 2 \qquad \implies \qquad Z^T has size 2 \times n
• y has size n \times 1 \qquad \implies \qquad Z^T y has size \, ( 2 \times n ) \times (n \times 1) = 2 \times 1

\begin{align*} Z^T y & = \left( \begin{array}{cc} 1 & x_1 \\ \ldots & \ldots\\ 1 & x_n \end{array} \right)^T \left( \begin{array}{l} y_1 \\ \ldots\\ y_n \end{array}\right) \\[15pt] & = \left( \begin{array}{ccc} 1 & \ldots & 1 \\ x_1 & \ldots & x_n \end{array} \right) \left( \begin{array}{l} y_1 \\ \ldots\\ y_n \end{array}\right) \\[15pt] & = \left(\begin{array}{c} 1 \times y_1 + 1 \times y_2 + \ldots + 1 \times y_n \\ x_1 y_1 + x_2 y_2 + \ldots + x_n y_n \end{array} \right) \\[15pt] & = \left( \begin{array}{c} n \overline{y} \\ \sum_{i=1}^n x_i y_i \end{array} \right) \end{align*}

Calculating Z^T Z

• Z has size n \times 2 \qquad \implies \qquad Z^T has size 2 \times n

• Therefore Z^T Z has size \, ( 2 \times n ) \times (n \times 2) = 2 \times 2

\begin{align*} Z^T Z & = \left( \begin{array}{cc} 1 & x_1 \\ \ldots & \ldots\\ 1 & x_n \end{array} \right)^T \left( \begin{array}{cc} 1 & x_1 \\ \ldots & \ldots\\ 1 & x_n \end{array} \right) \\[15pt] & = \left( \begin{array}{ccc} 1 & \ldots & 1 \\ x_1 & \ldots & x_n \end{array} \right) \left( \begin{array}{cc} 1 & x_1 \\ \ldots & \ldots\\ 1 & x_n \end{array} \right) \\[15pt] & = \left( \begin{array}{cc} 1 \times 1 + \ldots + 1 \times 1 & 1 \times x_1 + \ldots + 1 \times x_n \\ x_1 \times 1 + \ldots + x_n \times 1 & x_1 \times x_1 + \ldots + x_n \times x_n \end{array} \right) \\[15pt] & = \left( \begin{array}{cc} n & n \overline{x} \\ n \overline{x} & \sum_{i=1}^n x_i^2 \end{array} \right) \end{align*}

Matrix inverse: General formula

• Suppose to have a 2 \times n matrix

M = \left( \begin{array}{cc} a & b \\ c & d \end{array} \right)

• M is invertible iff

\det M = ad - bc \neq 0

• If \det M \neq 0, the inverse of M is

M^{-1} = \frac{1}{ ad - bc} \left( \begin{array}{cc} d & -b \\ -c & a \end{array}\right)

Resume the proof: Calculating (Z^T Z)^{-1}

\det \left( Z^T Z \right) = \det \left( \begin{array}{cc} n & n \overline{x} \\ n \overline{x} & \sum_{i=1}^n x_i^2 \end{array} \right) = n \sum_{i=1}^n x^2_i - n^2 \overline{x}^2 = n S_{xx}

• Note: \, S_{xx} = \sum_{i=1}^n (x_i - \overline{x})^2 = 0 \quad \iff \quad x_1 = \ldots = x_n = \overline{x}

• WLOG we can discard the trivial case S_{xx} = 0 because:

  • The predictors x_1, \ldots, x_n are either chosen, or random
  • If they are chosen, it makes no sense to choose them all equal
  • If they are random, they will all be equal with probability 0

• Therefore, we have \det \left( Z^T Z \right) = n S_{xx} > 0 \quad \implies \quad Z^T Z \, \text{ is invertible}

Calculating (Z^T Z)^{-1}

• Therefore, we assume S_{xx} > 0

• This way, we have

\det \left( Z^T Z \right) = n S_{xx} > 0

• Thus Z^T Z is invertible, with inverse

\begin{align*} (Z^T Z)^{-1} & = \left( \begin{array}{cc} n & n \overline{x} \\ n \overline{x} & \sum_{i=1}^n x_i^2 \end{array} \right)^{-1} \\[15pt] & = \frac{1}{n S_{xx} } \left( \begin{array}{cc} \sum_{i=1}^n x^2_i & -n \overline{x}\\ -n\overline{x} & n \end{array} \right) \end{align*}

Calculating (Z^T Z)^{-1} Z^T y

• (Z^T Z)^{-1} has size 2 \times 2

• Z^T y has size 2 \times 1

• (Z^T Z)^{-1} Z^T y therefore has dimensions (2 \times 2) \times (2 \times 1) = (2 \times 1)

• We expect (Z^T Z)^{-1} Z^T y to contain the simple regression estimators \hat \alpha, \hat \beta

(Z^T Z)^{-1} Z^T y = \left( \begin{array}{cc} \hat \alpha \\ \hat \beta \end{array} \right)

Calculating (Z^T Z)^{-1} Z^T y

• We have already computed (Z^T Z)^{-1} and Z^T y

• Their product is

(Z^T Z)^{-1} Z^T y = \frac{1}{n S_{xx} } \left( \begin{array}{cc} \sum_{i=1}^n x^2_i & -n \overline{x}\\ -n\overline{x} & n \end{array} \right) \left( \begin{array}{c} n \overline{y} \\ \sum_{i=1}^n x_i y_i \end{array} \right)

Calculating (Z^T Z)^{-1} Z^T y

• The first entry of (Z^T Z)^{-1} Z^T y is therefore

\begin{align*} \frac{ \sum_{i=1}^n x_i^2 n \overline{y} - n \overline{x} \sum_{i=1}^n x_i y_i }{n S_{xx}} & = \frac{ \sum_{i=1}^n x_i^2 \overline{y} - \overline{x} \sum_{i=1}^n x_i y_i }{ S_{xx}} \\[10pt] & = \frac{ \sum_{i=1}^n x_i^2 \overline{y} \textcolor{magenta}{- \overline{y} n \overline{x}^2 + \overline{y} n \overline{x}^2} - \overline{x} \sum_{i=1}^n x_i y_i }{ S_{xx}} \\[10pt] & = \overline{y} \ \frac{ \sum_{i=1}^n x_i^2 - n \overline{x}^2}{ S_{xx} } - \overline{x} \ \frac{ \sum_{i=1}^n x_i y_i - n \overline{x} \overline{y} }{ S_{xx} } \\[10pt] & = \overline{y} \ \frac{ S_{xx} }{ S_{xx} } - \overline{x} \ \frac{ S_{xy} }{ S_{xx} } \\[10pt] & = \overline{y} - \hat \beta \, \overline{x} = \hat{\alpha} \end{align*}

Calculating (Z^T Z)^{-1} Z^T y

• The second entry of (Z^T Z)^{-1} Z^T y is

\frac{ - n \overline{x} n \overline{y} + n \sum_{i=1}^n x_i y_i}{ n S_{xx} } = \frac{ \sum_{i=1}^n x_i y_i - n\overline{x} \overline{y} }{ S_{xx} } = \frac{ S_{xy} }{S_{xx}} = \hat{\beta}

• We have finally proven that

(Z^T Z)^{-1} Z^T y = \left( \begin{array}{cc} \hat \alpha \\ \hat \beta \end{array} \right)

• Conclusion
  • Simple linear regression is special case of general regression with p = 2
  • Estimator for general regression recovers estimators for simple regression

Part 4:
Multiple linear
regression

Mutiple linear regression

Response variable Y depends on p-1 predictors X_2, \ldots, X_p

• The goal is to learn the distribution of Y | X_2, \ldots, X_p

• Y | X_2, \ldots, X_p allows to predict values of Y, knowing values of X_2, \ldots, X_p

Note: We start counting from 2 for notational convenience

Mutiple linear regression model

Assumption: For each i=1, \ldots, n we assume given observations

• data point (x_{i2}, \ldots, x_{ip}, y_i)

• x_{ij} is from X_j

• y_i is from Y

• Denote by Y_i the random variable Y | x_{i2} ,\ldots, x_{ip}

Definition

The multiple linear regression model is Y_i = \beta_1 + \beta_2 x_{i2} + \ldots + \beta_p x_{ip} + \varepsilon_i where the residuals satisfy \varepsilon_1,\ldots, \varepsilon_n \,\, \text{ iid } \,\, N(0,\sigma^2)

Mutiple vs General linear regression

• Multiple linear regression is special case of general linear regression

• To see this, consider a general linear model with p parameters

Y_i = \beta_1 z_{i1} + \beta_2 z_{i2} + \ldots + \beta_p z_{ip} + \varepsilon_i \,, \qquad i = 1 , \ldots, n

• We want to compare the above to the multiple regression model

Y_i = \beta_1 + \beta_2 x_{i2} + \ldots + \beta_p x_{ip} + \varepsilon_i

• The 2 models are equivalent iff

z_{i1} = 1 \,, \qquad z_{i2} = x_{i2} \,, \qquad \ldots \qquad z_{ip} = x_{ip} \qquad \forall \, i = 1 , \ldots, n

Mutiple linear regression estimator

• Hence the design matrix Z and data vector y are

Z = \left( \begin{array}{cccc} 1 & x_{12} & \ldots & x_{1p} \\ 1 & x_{22} & \ldots & x_{2p} \\ \ldots & \ldots & \ldots & \ldots \\ 1 & x_{n2} & \ldots & x_{np} \\ \end{array} \right) \,, \qquad y = \left( \begin{array}{c} y_1 \\ \ldots \\ y_n \\ \end{array} \right) The design matrix includes a first column of 1s to account for the intercept

• Z has size n \times p

• y has size n \times 1

• The MLE for multiple regression is therefore \hat \beta \in \mathbb{R}^p \hat \beta = (Z^T Z)^{-1} Z^T y

Part 5:
Coefficient of
determination R^2

How good is the model?

• Consider the general linear regression model

Y_i = \beta_1 z_{i1} + \ldots + \beta_p \, z_{ip} + \varepsilon_i

• Given the observed values y = (y_1, \ldots, y_n), compute the MLE by

\hat \beta = (\hat \beta_1, \ldots, \hat \beta_p ) = (Z^T Z)^{-1} Z^T y

Problem

Quantify how well the model fits the observed values

y_1 , \ldots, y_n

• The predicted values are \hat y_i := {\rm I\kern-.3em E}[ Y | z_{i1}, \ldots , z_{ip} ] = \hat \beta_1 \, z_{i1} + \ldots + \hat \beta_p \, z_{ip} \quad \implies \quad \hat y = Z \hat \beta

• Recall: the Residual sum of squares is \mathop{\mathrm{RSS}}:= \sum_{i=1}^n ( y_i - \hat y_i )^2 \mathop{\mathrm{RSS}} measures deviation of predicted values from observed values

\text{Model is good } \,\, \iff \,\, \hat{y}_i \approx y_i \, \quad \forall \, i \,\, \iff \,\, \mathop{\mathrm{RSS}}\, \text{ is small}

• However: \mathop{\mathrm{RSS}} is a relative measure of precision
  • Need to rescale \mathop{\mathrm{RSS}}, which will lead to the coefficient of determination R^2
  • To this end, we need some preliminary results

Normal equation for General Regression

Lemma

Suppose given the general linear regression model

Y_i = \beta_1 z_{i1} + \ldots + \beta_p z_{ip} + \varepsilon_{i} for errors \varepsilon_1 , \ldots, \varepsilon_n iid N(0,\sigma^2). Define the observed errors \hat{\varepsilon}_i = y_i - \hat{y}_i Then the normal equation is satisfied \hat{\varepsilon}^T Z = \mathbf{0}

Proof

\begin{align*} \hat{\varepsilon}^T Z & = (y - \hat y)^T Z & \hat{\varepsilon} = y - \hat{y} \\ & = (y - Z \hat{\beta})^T Z & \hat{y} = Z\hat{\beta} \\ & = (y - Z (Z^T Z)^{-1} Z^T y)^T Z & \hat{\beta} = (Z^T Z)^{-1} Z^T y \\ & = y^T (I - Z (Z^T Z)^{-1} Z^T )^T Z & \text{factor } \,y \\ & = y^T (I - Z (Z^T Z)^{-1} Z^T )^T (Z^T)^T & Z = (Z^T)^T\\ & = y^T [ Z^T (I - Z (Z^T Z)^{-1} Z^T ) ]^T & (AB)^T = B^TA^T \\ & = y^T [ Z^T - \underbrace{Z^T Z (Z^T Z)^{-1}}_{I} \ Z^T ]^T \\[10pt] & = y^T \left[ Z^T - Z^T \right]^T = \mathbf{0} \end{align*}

Total sum of squares

• The total sum of squares is

\mathop{\mathrm{TSS}}:= \sum_{i=1}^n ( y_i - \overline{y} )^2

• \mathop{\mathrm{TSS}} measures deviation of observed values from the grand mean

• Hence \mathop{\mathrm{TSS}} measures variability of the observed data y_1 , \ldots, y_n

  • If data very variable, then usually y_i is far from \overline{y} \implies \mathop{\mathrm{TSS}} is large
  • If data not very variable, then y_i \approx \overline{y} \implies \mathop{\mathrm{TSS}} is small

Goal: Decompose the \mathop{\mathrm{TSS}}

\mathop{\mathrm{RSS}} and \mathop{\mathrm{ESS}}

• Recall: the Residual sum of squares is \mathop{\mathrm{RSS}}:= \sum_{i=1}^n ( y_i - \hat y_i )^2 The \mathop{\mathrm{RSS}} measures deviation of predicted values from observed values

• Introduce the explained sum of squares by \mathop{\mathrm{ESS}}:= \sum_{i=1}^n ( \hat y_i - \overline{y} )^2 \mathop{\mathrm{ESS}} measures deviation of predicted values from the grand mean

Decomposition of \mathop{\mathrm{TSS}}

Theorem

Suppose given the general linear regression model

Y_i = \beta_1 z_{i1} + \ldots + \beta_p z_{ip} + \varepsilon_{i} for errors \varepsilon_1 , \ldots, \varepsilon_n iid N(0,\sigma^2). Then

\mathop{\mathrm{TSS}}= \mathop{\mathrm{ESS}}+ \mathop{\mathrm{RSS}}- 2 \overline{y} \sum_{i=1}^n \hat{\varepsilon}_i where the observed errors are \hat{\varepsilon}_i = y_i - \hat{y}_i

Proof

Trick: Add and substract \hat{y}_i, then expand:

\begin{align*} \mathop{\mathrm{TSS}}& = \sum_{i=1}^n (y_i - \overline{y})^2 \\ & = \sum_{i=1}^n \left[ (\hat{y}_i - \overline{y}) + (y_i - \hat{y}_i) \right]^2 \\ & = \sum_{i=1}^n (\hat{y}_i - \overline{y})^2 + (y_i - \hat{y}_i)^2 + 2 (\hat{y}_i - \overline{y}) \underbrace{(y_i - \hat{y}_i)}_{\hat{\varepsilon}_i} \\ & = \mathop{\mathrm{ESS}}+ \mathop{\mathrm{RSS}}+ 2 \sum_{i=1}^n \hat{y}_i \hat{\varepsilon}_i - 2 \overline{y} \sum_{i=1}^n \hat{\varepsilon}_i \end{align*}

• Recall the normal equation

\hat{\varepsilon}^T Z = \mathbf{0}

• Using again that \hat y = Z \hat{\beta}, we get

\sum_{i=1}^n \hat{y}_i \hat{\varepsilon}_i = \hat{\varepsilon}^T \hat{y} = \hat{\varepsilon}^T Z \hat{\beta} = \mathbf{0} \hat{\beta} = 0

• From the above, we conclude the thesis: \mathop{\mathrm{TSS}}= \mathop{\mathrm{ESS}}+ \mathop{\mathrm{RSS}}+ 2 \underbrace{ \sum_{i=1}^n \hat{y}_i \hat{\varepsilon}_i}_{0} - 2 \overline{y} \sum_{i=1}^n \hat{\varepsilon}_i = \mathop{\mathrm{ESS}}+ \mathop{\mathrm{RSS}}- 2 \overline{y} \sum_{i=1}^n \hat{\varepsilon}_i

Multiple regression: \mathop{\mathrm{TSS}}= \mathop{\mathrm{ESS}}+ \mathop{\mathrm{RSS}}

Theorem

Suppose given the multiple regression linear model

Y_i = \beta_1 + \beta_2 x_{i2} + \ldots + \beta_p x_{ip} + \varepsilon_{i} for errors \varepsilon_1 , \ldots, \varepsilon_n iid N(0,\sigma^2). Then, the sum of errors is zero \sum_{i=1}^n \hat{\varepsilon}_i = 0 \,, where \hat{\varepsilon}_i = y_i - \hat{y}_i. In particular, the following decomposition holds \mathop{\mathrm{TSS}}= \mathop{\mathrm{ESS}}+ \mathop{\mathrm{RSS}}

Proof

• Since we are dealing with multiple linear regression, Z has the form

Z = \left( \begin{array}{cccc} 1 & x_{12} & \ldots & x_{1p} \\ 1 & x_{22} & \ldots & x_{2p} \\ \ldots & \ldots & \ldots & \ldots \\ 1 & x_{n2} & \ldots & x_{np} \\ \end{array} \right)

• Therefore, we have that

\hat{\varepsilon}^T Z = (\hat{\varepsilon}_1 , \ldots, \hat{\varepsilon}_n) \left( \begin{array}{cccc} 1 & x_{12} & \ldots & x_{1p} \\ 1 & x_{22} & \ldots & x_{2p} \\ \ldots & \ldots & \ldots & \ldots \\ 1 & x_{n2} & \ldots & x_{np} \\ \end{array} \right) = \left( \sum_{i=1}^n \hat{\varepsilon}_i , \ast , \ldots, \ast \right)

• The normal equation says that

\hat{\varepsilon}^T Z = \mathbf{0}

• Therefore, we conclude that

\hat{\varepsilon}^T Z = \left( \sum_{i=1}^n \hat{\varepsilon}_i , \ast , \ldots, \ast \right) = (0, 0, \ldots, 0)

• From the above, we infer that the sum of the errors is zero

\sum_{i=1}^n \hat{\varepsilon}_i = 0

• Multiple linear regression is a special case of general linear regression

• Therefore, we can apply the previous Theorem to get \mathop{\mathrm{TSS}}= \mathop{\mathrm{ESS}}+ \mathop{\mathrm{RSS}}- 2 \overline{y} \sum_{i=1}^n \hat{\varepsilon}_i

• In the previous slide we have shown that

\sum_{i=1}^n \hat{\varepsilon}_i = 0

• Therefore, the thesis follows

\mathop{\mathrm{TSS}}= \mathop{\mathrm{ESS}}+ \mathop{\mathrm{RSS}}- 2 \overline{y} \sum_{i=1}^n \hat{\varepsilon}_i = \mathop{\mathrm{ESS}}+ \mathop{\mathrm{RSS}}

Coefficient of determination R^2

Consider the general linear regression model Y_i = \beta_1 z_{i1} + \ldots + \beta_p \, z_{ip} + \varepsilon_i For observed data y = (y_1, \ldots, y_n), define the predictions by \hat{y} = Z\hat{\beta} \,, \qquad \hat{\beta} = (Z^TZ)^{-1} Z^T y

Definition

The coefficient of determination is R^2 := 1 - \frac{ \mathop{\mathrm{RSS}}}{ \mathop{\mathrm{TSS}}} = 1 - \frac{ \sum_{i=1}^n ( y_i - \hat y_i )^2 }{ \sum_{i=1}^n ( y_i - \overline{y} )^2 }

Properties of R^2

Proposition

For the general linear regression model, we have that

R^2 \leq 1

Moreover

R^2 = 1 \qquad \iff \qquad y_i = \hat y_i \quad \,\, \forall \, i = 1 , \ldots, n

Proof

• Since \mathop{\mathrm{RSS}} and \mathop{\mathrm{TSS}} are sums of squares, we have that \mathop{\mathrm{TSS}}, \, \mathop{\mathrm{RSS}}\geq 0

• Therefore, the first part of the statemet follows immediately R^2 := 1 - \frac{\mathop{\mathrm{RSS}}}{\mathop{\mathrm{TSS}}} \leq 1

• Moreover, recalling the definition of \mathop{\mathrm{RSS}}, we have that \mathop{\mathrm{RSS}}= \sum_{i=1}^n (y_i - \hat{y}_i)^2 = 0 \quad \iff \quad \hat{y}_i = y_i \quad \forall \, i

• The thesis immediately follows: R^2 = 1 \,\, \iff \,\, 1 - \frac{\mathop{\mathrm{RSS}}}{\mathop{\mathrm{TSS}}} = 1 \,\, \iff \,\, \mathop{\mathrm{RSS}}= 0 \,\, \iff \,\, \hat{y}_i = y_i \quad \forall \, i

R^2 might be negative

Proposition

1. For the general linear regression model, it might hold that R^2 < 0

2. For the multiple regression model, it always holds that 0 \leq R^2 \leq 1

Bottom line:

• R^2 can be negative for general regression (i.e. when no intercept is present)

• 0 \leq R^2 \leq 1 for multiple regression (i.e. when intercept is present)

Proof

1. For general linear regression, the following decomposition holds (Thm Slide 85) \mathop{\mathrm{TSS}}= \mathop{\mathrm{ESS}}+ \mathop{\mathrm{RSS}}- 2 \overline{y} \sum_{i=1}^n \hat{\varepsilon}_i

• By definition of R^2, we have R^2 := 1 - \frac{ \mathop{\mathrm{RSS}}}{ \mathop{\mathrm{TSS}}} = \underbrace{\frac{\mathop{\mathrm{ESS}}}{\mathop{\mathrm{TSS}}}}_{\geq 0} - \underbrace{\frac{2 \overline{y} \sum_{i=1}^n \hat{\varepsilon}_i}{\mathop{\mathrm{TSS}}}}_{\text{can have any sign}}

• Since the last term can have any sign, it might hold that R^2 < 0

2. For multiple linear regression, the following decomposition holds (Thm Slide 88) \mathop{\mathrm{TSS}}= \mathop{\mathrm{ESS}}+ \mathop{\mathrm{RSS}}

• By definition of R^2, we have

R^2 := 1 - \frac{ \mathop{\mathrm{RSS}}}{ \mathop{\mathrm{TSS}}} = \frac{\mathop{\mathrm{ESS}}}{\mathop{\mathrm{TSS}}} \geq 0

• Therefore, we conclude that

0 \leq R^2 \leq 1

Conclusion

We have shown that

• R^2 \leq 1

• R^2 = 1 \quad \iff \quad y_i = \hat y_i \quad \,\, \forall \, i = 1 , \ldots, n

Conclusion: R^2 measures how well the model fits the data

R^2 \, \text{ close to } \, 1 \quad \implies \quad \text{ model fits data well}

Warning: R^2 can be negative for general regression (no intercept)

Part 6:
Example of
multiple regression

Example: Predicting unemployment

Goal: Predict unemployment rates

• Unemp. related to Productivity Index
• Other factors might also play a role
• These factors likely depend on the year
• Use year as surrogate for other factors

Unemp.	Product.	Year
3.1	113	1950
1.9	123	1951
1.7	127	1952
1.6	138	1953
3.2	130	1954
2.7	146	1955
2.6	151	1956
2.9	152	1957
4.7	141	1958
3.8	159	1959

Enter the data

• Enter the data in 3 vectors

# Unemployment data
unemployment <- c(3.1, 1.9, 1.7, 1.6, 3.2, 2.7, 2.6, 2.9, 4.7, 3.8)

# Productivity data
productivity <- c(113, 123, 127, 138, 130, 146, 151, 152, 141, 159)

# Year data
year <- seq(1950, 1959, by = 1)

Plotting the data

• Want to see if either Productivity or Year predict Unemployment. Therefore, plot
  • Productivity Vs Unemployment
  • Year Vs Unemployment

# Set up the layout with two plot panels side by side
par(mfrow = c(1, 2))

# Scatter plot: Productivity vs Unemployment
plot(productivity, unemployment, 
     xlab = "Productivity", ylab = "Unemployment",
     main = "Productivity vs Unemployment", 
     pch = 16)

# Scatter plot: Year vs Unemployment
plot(year, unemployment, 
     xlab = "Year", ylab = "Unemployment",
     main = "Year vs Unemployment", 
     pch = 16)

Output

There appears to be some linear relationship

Plotting the data in 3D

To better understand the data we can do a 3D scatter plot using either

• scatterplot3D
  • installed via install.packages("scatterplot3d")
  • produces static plots
• plotly
  • installed via install.packages("plotly")
  • produces interactive plots

Plotting the data with scatterplot3d

# Load the scatterplot3d library
library(scatterplot3d)

# Create 3D scatter plot
scatterplot3d(x = productivity,
              y = year,
              z = unemployment, 
              main = "Productivity and Year vs Unemployment", 
              xlab = "Productivity", 
              ylab = "Year", 
              zlab = "Unemployment",
              pch = 16,
              color = "black",
              angle = 50)

Plotting the data with scatterplot3d

The data is clearly close to a plane

Plotting the data with plotly

# Load the plotly library
library(plotly)

# Create a scatter plot using plot_ly
plot_ly(x = productivity, 
        y = year, 
        z = unemployment, 
        type = "scatter3d", 
        mode = "markers",
        marker = list(size = 5, color = "black")) %>%
  layout(scene = list(xaxis = list(title = "Productivity"),
                      yaxis = list(title = "Year"),
                      zaxis = list(title = "Unemployment")),
         width = 1000, 
         height = 500)

Plotting the data with plotly

The data is clearly close to a plane

Setting up multiple regression model

• We saw that the data points ( \text{Productivity}, \text{Year}, \text{Unemployment} ) \in R^3 roughly lie on a plane

• Goal: Use multiple regression to compute such plane

  • Unemployment is modelled by response variable Y
  • Productivity is modelled by predictor X_2
  • Year is modelled by predictor X_3
  • The multiple regression model is {\rm I\kern-.3em E}[Y | x_2, x_3] = \beta_1 + \beta_2 \, x_2 + \beta_3 \, x_3

Exercise

Multiple regression model is {\rm I\kern-.3em E}[Y | x_2, x_3] = \beta_1 + \beta_2 \, x_2 + \beta_3 \, x_3

• Enter design matrix Z into R
• Enter data y into R
• Compute estimator \hat \beta = (Z^T Z)^{-1} Z^T y
  • Matrix product in R is \,%*%
  • Transpose matrix of \,A\, is \,t(A)
  • Inverse of matrix \,A\, is \,solve(A)

Unemp.	Product.	Year
y_i	x_{i2}	x_{i3}
3.1	113	1950
1.9	123	1951
1.7	127	1952
1.6	138	1953
3.2	130	1954
2.7	146	1955
2.6	151	1956
2.9	152	1957
4.7	141	1958
3.8	159	1959

Solution

The design matrix is Z=\left(\begin{array}{cccc} 1 & 113 & 1950 \\ 1 & 123 & 1951 \\ 1 & 127 & 1952 \\ 1 & 138 & 1953 \\ 1 & 130 & 1954 \\ 1 & 146 & 1955 \\ 1 & 151 & 1956 \\ 1 & 152 & 1957 \\ 1 & 141 & 1958 \\ 1 & 159 & 1959 \\ \end{array}\right)

Unemp.	Product.	Year
y_i	x_{i2}	x_{i3}
3.1	113	1950
1.9	123	1951
1.7	127	1952
1.6	138	1953
3.2	130	1954
2.7	146	1955
2.6	151	1956
2.9	152	1957
4.7	141	1958
3.8	159	1959

Solution

The data vector is y = \left(\begin{array}{c} 3.1 \\ 1.9 \\ 1.7 \\ 1.6 \\ 3.2 \\ 2.7 \\ 2.6 \\ 2.9 \\ 4.7 \\ 3.8 \\ \end{array}\right)

Unemp.	Product.	Year
y_i	x_{i2}	x_{i3}
3.1	113	1950
1.9	123	1951
1.7	127	1952
1.6	138	1953
3.2	130	1954
2.7	146	1955
2.6	151	1956
2.9	152	1957
4.7	141	1958
3.8	159	1959

Solution

• Data vector y is stored in R as usual

# Store vector y
y <- c(3.1, 1.9, 1.7, 1.6, 3.2, 2.7, 2.6, 2.9, 4.7, 3.8)

• Design matrix is stored as follows

# Store design matrix Z as long vector
Z <- c(1, 113, 1950,
       1, 123, 1951,
       1, 127, 1952,
       1, 138, 1953,
       1, 130, 1954,
       1, 146, 1955,
       1, 151, 1956,
       1, 152, 1957,
       1, 141, 1958,
       1, 159, 1959)

# Make Z into a matrix with 3 columns
Z <- matrix(Z, ncol = 3, byrow = TRUE)

Solution

• We need to compute the estimator

\hat \beta = (Z^T Z)^{-1} Z^T y

• The matrix transpose is computed with \,t(A)
• The product of two matrices A and B is computed with \, A %*% B
• We use these two operators to compute Z^T Z and store it into m1

# Calculate m1
m1 <- t(Z) %*% Z

Solution

• The inverse of a matrix A is computed with \, solve(A)
• We use this function to compute (Z^T Z)^{-1} and store it into m2

# Calculate m2
m2 <- solve(m1)

• We can compute Z^T y with \,%*%
• This is because R automatically interprets vectors as matrices

# Calculate m3
m3 <- t(Z) %*% y

Solution

• We compute the estimator \hat{\beta}=(Z^T Z)^{-1} Z^T y and store it as \, beta

# Calculate estimator beta
beta <- m2 %*% m3

• We then print the result to screen

# Print estimator beta
cat("The estimator is", beta)

The estimator is -1271.75 -0.1033386 0.6594171

Solution

• The computed regression model is

\begin{align*} {\rm I\kern-.3em E}[Y | x_2, x_3] & = \hat\beta_1 + \hat\beta_2 \, x_2 + \hat\beta_3 \, x_3 \\[15pt] & = -1271.75 + (-0.1033386) \times x_2 + 0.6594171 \times x_3 \end{align*}

• This means

\begin{align*} \text{Predicted Unemployment} = -1271.75 & + (-0.1033386) \times \text{Productivity} \\[15pt] & + (0.6594171) \times \text{Year} \end{align*}

• Previous code can be downloaded here multiple_regression.R

Plot of data and regression plane

# Load the plotly library
library(plotly)

# Data
unemployment <- c(3.1, 1.9, 1.7, 1.6, 3.2, 2.7, 2.6, 2.9, 4.7, 3.8)
productivity <- c(113, 123, 127, 138, 130, 146, 151, 152, 141, 159)
year <- seq(1950, 1959, by = 1)

# Generate a grid of x and y values
x_grid <- seq(min(productivity), max(productivity), length.out = 50)
y_grid <- seq(min(year), max(year), length.out = 50)
grid <- expand.grid(productivity = x_grid, year = y_grid)

# Calculate z values for the regression plane
z_values <- -1271.75 - 0.1033386 * grid$productivity + 0.6594171 * grid$year

# Create a scatter plot using plot_ly
plot_ly(x = productivity, 
        y = year, 
        z = unemployment, 
        type = "scatter3d", 
        mode = "markers",
        marker = list(size = 5, color = "black")) %>%
  layout(scene = list(xaxis = list(title = "Productivity"),
                      yaxis = list(title = "Year"),
                      zaxis = list(title = "Unemployment")),
         width = 1000, 
         height = 500) %>%
         add_surface(
         x = x_grid, 
         y = y_grid, 
         z = matrix(z_values, nrow = length(x_grid)),
         opacity = 0.5, 
         colorscale = list(c(0, 'rgb(255,255,255)'), c(1, 'rgb(255,0,0)')))

Computing the R^2 coefficient

• How well does the multiple linear model fit our data?

• To answer this question we compute the coefficient of determination

R^2 = 1 - \frac{\mathop{\mathrm{RSS}}}{\mathop{\mathrm{TSS}}}

Computing \mathop{\mathrm{TSS}}

• We have that

\mathop{\mathrm{TSS}}:= \sum_{i=1}^n (y_i - \overline{y})^2

• We compute \overline{y} with the R command

# Compute mean of y
y.bar <- mean(y)

• We compute \mathop{\mathrm{TSS}} with the R command

# Compute TSS
TSS <- sum( ( y - y.bar) ^ 2 )

Computing predictions

• We have that

\mathop{\mathrm{RSS}}:= \sum_{i=1}^n (y_i - \hat y_i)^2

• We need to compute the predictions

\hat y_i := \hat \beta_1 + \hat \beta_2 x_{i2} + \hat \beta_3 x_{i3}

Computing predictions

• \hat y, the design matrix Z, and \hat \beta are

\hat y = \left(\begin{array}{c} \hat y_1 \\ \ldots \\ \hat y_i \\ \ldots \\ \hat y_n \\ \end{array}\right) \,, \qquad Z = \left(\begin{array}{cccc} 1 & x_{11} & x_{12} \\ \ldots & \ldots & \ldots \\ 1 & x_{i1} & x_{i2} \\ \ldots & \ldots & \ldots \\ 1 & x_{n1} & x_{n2} \\ \end{array}\right) \,, \qquad \hat \beta = \left(\begin{array}{c} \hat \beta_1 \\ \hat \beta_2 \\ \hat \beta_3 \\ \end{array}\right)

• Therefore, we can compute \hat y_i = \hat \beta_1 + \hat \beta_2 x_{i2} + \hat \beta_3 x_{i3} with the product \hat y = Z \hat \beta

Computing \mathop{\mathrm{RSS}}

• Recall that \hat \beta is stored in beta

• Compute predictions \hat y = Z \hat{\beta}

# Compute predictions y.hat
y.hat <- Z %*% beta

• Recall that \mathop{\mathrm{RSS}}= \sum_{i=1}^n (y_i - \hat{y}_i)^2

• This is computed in R with

# Compute RSS
RSS <- sum( (y - y.hat) ^ 2 )

Computing R^2

• The coefficient R^2 is computed with

# Compute coefficient of determination R^2
R2 <- 1 - RSS / TSS

# Print R^2
cat("\nThe coefficient of determination R^2 is", R2)

• The full code can be downloaded here R2_multiple_regression.R

Output & Conclusions

The estimator is -1271.75 -0.1033386 0.6594171

The coefficient of determination R^2 is 0.8655401

The coefficient of determination R^2 = 0.8655401 is quite close to 1, showing that:

• The model fits data quite well
• Productivity Index and Year affect Unemployment
• Unemployment is almost completely explained by Productivity Index and Year
  (Because R^2 is almost 1)

Part 6:
Two sample t-test
as general regression

Two-sample t-test as general regression

• Two-sample t-test is special case of general linear regression

• This example is important for two reasons

  • Shows that multiple linear regression encapsulates simple models like the two-sample t-test
  • Shows that general linear regression leads to intuitive solutions in simple examples

Two-sample t-test setting

• We have 2 populations A and B distributed like N(\mu_A, \sigma_A^2) and N(\mu_B, \sigma_B^2)

• We have two samples

  • Sample of size n_A from population A a = (a_1, \ldots, a_{n_A})
  • Sample of size n_B from population B b = (b_1, \ldots, b_{n_B})

• Two-sample t-test compares means \mu_A and \mu_B by computing t-statistic t = \frac{ \overline{a} - \overline{b} }{\mathop{\mathrm{e.s.e.}}}

Setting up the regression analysis

• We want a regression model that can describe the sample means \overline{a} and \overline{b}

• It is sufficient to consider a general linear model with p = 2, that is,

{\rm I\kern-.3em E}[Y | Z_1 = z_1 , Z_2 = z_2 ] = \beta_1 z_1 + \beta_2 z_2

• Define the data vector y by concatenating a and b

y = \left(\begin{array}{c} y_1 \\ \ldots \\ y_{n_A} \\ y_{n_A + 1}\\ \ldots \\ y_{n_A + n_B} \end{array}\right) = \left(\begin{array}{c} a_1 \\ \ldots \\ a_{n_A} \\ b_{1}\\ \ldots \\ b_{n_B} \end{array}\right)

Setting up the regression analysis

• The variable Z_1 is modelled as

Z_1 = 1_{A}(i) := \begin{cases} 1 & \text{ if i-th observation is from population A} \\ 0 & \text{ otherwise} \end{cases}

• Therefore, we have

\begin{align*} z_1 & = (\underbrace{1_A(i) , \ldots, 1_A(i)}_{n_A + n_B} ) \\[15pts] & = (\underbrace{1 , \ldots, 1}_{n_A}, \underbrace{0 , \ldots, 0}_{n_B} ) \end{align*}

Setting up the regression analysis

• Similarly, the variable Z_2 is modelled as

Z_2 = 1_{B}(i) := \begin{cases} 1 & \text{ if i-th observation is from population B} \\ 0 & \text{ otherwise} \end{cases}

• Therefore we have

\begin{align*} z_2 & = (\underbrace{1_B(i), \ldots, 1_B (i)}_{n_A + n_B} ) \\[15pts] & = (\underbrace{0 , \ldots, 0}_{n_A}, \underbrace{1 , \ldots, 1}_{n_B} ) \end{align*}

Setting up the regression analysis

• The general regression model is

Y_i = \beta_1 \, 1_{A}(i) + \beta_2 \, 1_{B}(i) + \varepsilon_i

• Variables 1_A and 1_B are called dummy variables (more on this later)

• The design matrix is therefore

Z = (1_A | 1_B) = \left(\begin{array}{cc} 1_A(i) & 1_B (i) \\ \ldots & \ldots\\ 1_A(i) & 1_B (i) \\ \end{array}\right) = \left(\begin{array}{cc} 1 & 0 \\ \ldots & \ldots\\ 1 & 0\\ 0 & 1 \\ \ldots & \ldots\\ 0 & 1 \end{array}\right)

Calculating Z^T y

• We want to compute the regression estimator

\hat \beta = (Z^T Z)^{-1} Z^T y

• Z has dimension (n_A + n_B) \times 2
• Z^T has dimension 2 \times (n_A + n_B)
• y has dimension (n_A + n_B) \times 1
• Z^T y therefore has dimension

[ 2 \times (n_A + n_B)] \times [ (n_A + n_B) \times 1 ] = 2 \times 1

Calculating Z^T y

\begin{align*} Z^T y & = \left(\begin{array}{cc} 1 & 0 \\ \ldots & \ldots\\ 1 & 0\\ 0 & 1\\ \ldots & \ldots\\ 0 & 1 \end{array}\right)^T \left(\begin{array}{c} y_1 \\ \ldots\\ y_{n_A}\\ y_{n_A+1}\\ \ldots\\ y_{n_A+n_B} \end{array}\right) = \left(\begin{array}{cccccc} 1 & \ldots & 1 & 0 & \ldots & 0 \\ 0 & \ldots & 0 & 1 & \ldots & 1 \\ \end{array}\right) \left(\begin{array}{c} y_1 \\ \ldots\\ y_{n_A}\\ y_{n_A+1}\\ \ldots\\ y_{n_A+n_B} \end{array}\right) \\[35pt] & = \left(\begin{array}{c} y_1 \cdot 1 + \ldots + y_{n_A} \cdot 1 + y_{n_A + 1} \cdot 0 + \ldots + y_{n_A + n_B} \cdot 0 \\ y_1 \cdot 0 + \ldots + y_{n_A} \cdot 0 + y_{n_A + 1} \cdot 1 + \ldots + y_{n_A + n_B} \cdot 1 \end{array}\right) \\[20pt] & = \left(\begin{array}{c} y_1 + \ldots + y_{n_A} \\ y_{n_A + 1} + \ldots + y_{n_A + n_B} \end{array}\right) = \left(\begin{array}{c} a_1 + \ldots + a_{n_A} \\ b_{1} + \ldots + b_{n_B} \end{array}\right) = \left(\begin{array}{c} n_A \ \overline{a} \\ n_B \ \overline{b} \end{array}\right) \end{align*}

Calculating Z^T Z

• Z has dimension (n_A + n_B) \times 2
• Z^T has dimension 2 \times (n_A + n_B)
• Z^T Z therefore has dimension

[ 2 \times (n_A + n_B)] \times [ (n_A + n_B) \times 2 ] = 2 \times 2

Calculating Z^T Z

\begin{align*} Z^T Z & = \left(\begin{array}{cc} 1 & 0 \\ \ldots & \ldots\\ 1 & 0\\ 0 & 1\\ \ldots & \ldots\\ 0 & 1 \end{array}\right)^T \left(\begin{array}{cc} 1 & 0 \\ \ldots & \ldots\\ 1 & 0\\ 0 & 1\\ \ldots & \ldots\\ 0 & 1 \end{array}\right) \\[35pt] & = \left(\begin{array}{cccccc} 1 & \ldots & 1 & 0 & \ldots & 0 \\ 0 & \ldots & 0 & 1 & \ldots & 1 \\ \end{array}\right) \left(\begin{array}{cc} 1 & 0 \\ \ldots & \ldots\\ 1 & 0\\ 0 & 1\\ \ldots & \ldots\\ 0 & 1 \end{array}\right) = \left(\begin{array}{cc} n_A & 0 \\ 0 & n_B \end{array}\right) \end{align*}

Calculating \hat \beta

• As Z^T Z is diagonal, the inverse is

(Z^T Z)^{-1} = \left(\begin{array}{cc} n_A & 0 \\ 0 & n_B \end{array}\right)^{-1} =\left(\begin{array}{cc} \frac{1}{n_A} & 0 \\ 0 & \frac{1}{n_B} \end{array}\right)

• The MLE is therefore

\hat \beta = (Z^T Z)^{-1} Z^Ty = \left(\begin{array}{cc} \frac{1}{n_A} & 0 \\ 0 & \frac{1}{n_B} \end{array}\right) \left(\begin{array}{c} n_A \ \overline{a} \\ n_B \ \overline{b} \end{array}\right) = \left(\begin{array}{c} \overline{a} \\ \overline{b} \end{array}\right)

Conclusions

• The MLE is

\hat \beta = \left(\begin{array}{c} \overline{a} \\ \overline{b} \end{array}\right)

• The regression function is hence

\begin{align*} {\rm I\kern-.3em E}[Y | 1_A = z_1 , 1_B = z_2] & = \hat\beta_1 \ z_1 + \hat\beta_2 \ z_2 \\[20pt] & = \overline{a} \ z_1 + \overline{b} \ z_2 \end{align*}

Conclusions

• This is a very intuitive result:
  • The expected value for Y when data is observed from population A is {\rm I\kern-.3em E}[Y | 1_A = 1 , 1_B = 0] = \overline{a}
  • The expected value for Y when data is observed from population B is {\rm I\kern-.3em E}[Y | 1_A = 0 , 1_B = 1] = \overline{b}
• Therefore, under this simple model
  • The best estimate for population A is the sample mean \overline{a}
  • The best estimate for population B is the sample mean \overline{b}