Statistical Models

Lecture 6

Dr. Silvio Fanzon
S.Fanzon@hull.ac.uk

University of Hull

Lecture 6:
Contingency tables &
Simulation

Outline of Lecture 6

  1. Goodness-of-fit test for Contingency tables
  2. Worked Example
  3. Chi-squared test of independence
  4. Worked Example
  1. Monte Carlo simulations
  2. Simulating p-values
  3. The Bootstrap

Part 1:
Goodness-of-fit test for
Contingency tables

Two-way Contigency Tables: Table in which each observation is classified in 2 ways

Example:

  • Relative performance of Man Utd managers

  • Two classifications for each game: Result, and Manager in charge

Manager Won Drawn Lost
Moyes 27 9 15
Van Gaal 54 25 24
Mourinho 84 32 28
Solskjaer 91 37 40
Rangnick 11 10 8
ten Hag 61 12 28

Contingency tables: Abstract definition

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 O_{11} O_{12} \ldots O_{1C} O_{1+}
X = 2 O_{21} O_{22} \ldots O_{2C} O_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R O_{R1} O_{R2} \ldots O_{RC} O_{R+}
Totals O_{+1} O_{+2} \ldots O_{+C} m
  • Each observation
    • has attached two categories X and Y
    • can only belong to one category (X,Y) = (i,j)
  • O_{ij} is the count of observations with (X,Y) = (i,j)
  • Table has R rows and C columns, for total of n = RC categories

Contingency tables: Abstract definition

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 O_{11} O_{12} \ldots O_{1C} O_{1+}
X = 2 O_{21} O_{22} \ldots O_{2C} O_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R O_{R1} O_{R2} \ldots O_{RC} O_{R+}
Totals O_{+1} O_{+2} \ldots O_{+C} m
  • plus symbol in subscript denotes sum over that subscript. Example

O_{R+} = \sum_{j=1}^C O_{Rj} \qquad \quad O_{+2} = \sum_{i=1}^R O_{i2}

Contingency tables: Abstract definition

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 O_{11} O_{12} \ldots O_{1C} O_{1+}
X = 2 O_{21} O_{22} \ldots O_{2C} O_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R O_{R1} O_{R2} \ldots O_{RC} O_{R+}
Totals O_{+1} O_{+2} \ldots O_{+C} m
  • The total count is

m = O_{++} = \sum_{i=1}^R \sum_{j=1}^C O_{ij}

Contingency tables: Abstract definition

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 O_{11} O_{12} \ldots O_{1C} O_{1+}
X = 2 O_{21} O_{22} \ldots O_{2C} O_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R O_{R1} O_{R2} \ldots O_{RC} O_{R+}
Totals O_{+1} O_{+2} \ldots O_{+C} m
  • The marginal counts sum to m as well

\sum_{i=1}^R O_{i+} = \sum_{i=1}^R \sum_{j=1}^C O_{ij} = m

Contingency tables: Abstract definition

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 O_{11} O_{12} \ldots O_{1C} O_{1+}
X = 2 O_{21} O_{22} \ldots O_{2C} O_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R O_{R1} O_{R2} \ldots O_{RC} O_{R+}
Totals O_{+1} O_{+2} \ldots O_{+C} m
  • The marginal counts sum to m as well

\sum_{j=1}^C O_{+j} = \sum_{j=1}^C \sum_{i=1}^R O_{ij} = m

Contingency tables: Probabilities

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 p_{11} p_{12} \ldots p_{1C} p_{1+}
X = 2 p_{21} p_{22} \ldots p_{2C} p_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R p_{R1} p_{R2} \ldots p_{RC} p_{R+}
Totals p_{+1} p_{+2} \ldots p_{+C} 1
  • Observation in cell (i,j) happens with probability

p_{ij} := P(X = i , Y = j)

Contingency tables: Probabilities

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 p_{11} p_{12} \ldots p_{1C} p_{1+}
X = 2 p_{21} p_{22} \ldots p_{2C} p_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R p_{R1} p_{R2} \ldots p_{RC} p_{R+}
Totals p_{+1} p_{+2} \ldots p_{+C} 1
  • The marginal probabilities that X = i or Y = j are at the margins of table

P(X = i) = \sum_{j=1}^C P(X = i , Y = j) = \sum_{j=1}^C p_{ij} = p_{i+}

Contingency tables: Probabilities

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 p_{11} p_{12} \ldots p_{1C} p_{1+}
X = 2 p_{21} p_{22} \ldots p_{2C} p_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R p_{R1} p_{R2} \ldots p_{RC} p_{R+}
Totals p_{+1} p_{+2} \ldots p_{+C} 1
  • The marginal probabilities that X = i or Y = j are at the margins of table

P(Y = j) = \sum_{i=1}^R P(X = i , Y = j) = \sum_{i=1}^R p_{ij} = p_{+j}

Contingency tables: Probabilities

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 p_{11} p_{12} \ldots p_{1C} p_{1+}
X = 2 p_{21} p_{22} \ldots p_{2C} p_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R p_{R1} p_{R2} \ldots p_{RC} p_{R+}
Totals p_{+1} p_{+2} \ldots p_{+C} 1
  • Marginal probabilities sum to 1

\sum_{i=1}^R p_{i+} = \sum_{i=1}^R P(X = i) = \sum_{i=1}^R \sum_{j=1}^C P(X = i , Y = j) = 1

Contingency tables: Probabilities

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 p_{11} p_{12} \ldots p_{1C} p_{1+}
X = 2 p_{21} p_{22} \ldots p_{2C} p_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R p_{R1} p_{R2} \ldots p_{RC} p_{R+}
Totals p_{+1} p_{+2} \ldots p_{+C} 1
  • Marginal probabilities sum to 1

\sum_{j=1}^C p_{+j} = \sum_{j=1}^C P(X = j) = \sum_{j=1}^R \sum_{j=1}^C P(X = i , Y = j) = 1

Multinomial distribution

  • Counts O_{ij} and probabilities p_{ij} can be assembled into R \times C matrices O = \left( \begin{array}{ccc} O_{11} & \ldots & O_{1C} \\ \vdots & \ddots & \vdots \\ O_{R1} & \ldots & O_{RC} \\ \end{array} \right) \qquad \qquad p = \left( \begin{array}{ccc} p_{11} & \ldots & p_{1C} \\ \vdots & \ddots & \vdots \\ p_{R1} & \ldots & p_{RC} \\ \end{array} \right)

  • This way the random matrix O has multinomial distribution O \sim \mathop{\mathrm{Mult}}(m,p)

  • The counts O_{ij} are therefore binomial O_{ij} \sim \mathop{\mathrm{Bin}}(m,p_{ij})

Multinomial distribution

  • We can also consider the marginal random vectors (O_{1+}, \ldots, O_{R+}) \qquad \qquad (O_{+1}, \ldots, O_{+C})

  • These have also multinomial distribution (O_{1+}, \ldots, O_{R+}) \sim \mathop{\mathrm{Mult}}(m, p_{1+}, \ldots, p_{R+}) (O_{+1}, \ldots, O_{+C}) \sim \mathop{\mathrm{Mult}}(m, p_{+1}, \ldots, p_{+C})

Expected counts

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 O_{11} O_{12} \ldots O_{1C} O_{1+}
X = 2 O_{21} O_{22} \ldots O_{2C} O_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R O_{R1} O_{R2} \ldots O_{RC} O_{R+}
Totals O_{+1} O_{+2} \ldots O_{+C} m
  • We have that O_{ij} \sim \mathop{\mathrm{Bin}}(m,p_{ij})
  • We model the expected counts for category (i,j) as E_{ij} := {\rm I\kern-.3em E}[O_{ij}] = m p_{ij}

Marginal expected counts

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 E_{11} E_{12} \ldots E_{1C} E_{1+}
X = 2 E_{21} E_{22} \ldots E_{2C} E_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R E_{R1} E_{R2} \ldots E_{RC} E_{R+}
Totals E_{+1} E_{+2} \ldots E_{+C} m
  • Due to linearity of expectation, it makes sense to define marginal counts E_{i+} := \sum_{j=1}^C E_{ij} \qquad \qquad E_{+j} := \sum_{i=1}^R E_{ij}

Marginal expected counts

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 E_{11} E_{12} \ldots E_{1C} E_{1+}
X = 2 E_{21} E_{22} \ldots E_{2C} E_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R E_{R1} E_{R2} \ldots E_{RC} E_{R+}
Totals E_{+1} E_{+2} \ldots E_{+C} m
  • Marginal expected counts sum to m. For example: \sum_{i=1}^R E_{i+} = \sum_{i=1}^R \sum_{j=1}^C E_{ij} = m \sum_{i=1}^R \sum_{j=1}^C p_{ij} = m

The chi-squared statistic

Y = 1 Y = 2 \ldots Y = C Totals
X = 1 O_{11} O_{12} \ldots O_{1C} O_{1+}
X = 2 O_{21} O_{22} \ldots O_{2C} O_{2+}
\cdots \cdots \cdots \ldots \cdots \cdots
X = R O_{R1} O_{R2} \ldots O_{RC} O_{R+}
Totals O_{+1} O_{+2} \ldots O_{+C} m

Definition
The chi-squared statistic associated to the above contingency table is \chi^2 := \sum_{i=1}^R \sum_{j=1}^C \frac{ (O_{ij} - E_{ij})^2 }{ E_{ij} } = \sum_{i=1}^R \sum_{j=1}^C \frac{ (O_{ij} - m p_{ij})^2 }{ m p_{ij} }

Distribution of chi-squared statistic

Theorem

Suppose the counts O \sim \mathop{\mathrm{Mult}}(m,p). Then \chi^2 = \sum_{i=1}^R \sum_{j=1}^C \frac{ (O_{ij} - m p_{ij})^2 }{ m p_{ij} } \ \stackrel{ {\rm d} }{ \longrightarrow } \ \chi_{RC - 1 - {\rm fitted} }^2 when sample size m \to \infty. The convergence is in distribution and

  • \rm fitted = \, # of parameters used to estimate cell probabilities p_{ij}

Quality of approximation: The chi-squared approximation is good if E_{ij} = m p_{ij} \geq 5 \quad \text{ for all } \,\, i = 1 , \ldots , R \, \text{ and } j = 1, \ldots, C

Goodness-of-fit test for contingency tables

Setting:

  • Population consists of items of n = R \times C different types

  • p_{ij} is probability that an item selected at random is of type (i,j)

  • p_{ij} is unknown and needs to be estimated

  • As guess for p_{ij} we take p_{ij}^0 such that 0 \leq p_{ij}^0 \leq 1 \qquad \qquad \sum_{i=1}^R \sum_{j=1}^C p_{ij}^0 = 1

Goodness-of-fit test for contingency tables

Hypothesis Test: We test for equality of p_{ij} to p_{ij}^0 \begin{align*} & H_0 \colon p_{ij} = p_{ij}^0 \qquad \text{ for all } \, i = 1, \ldots, R \,, \text{ and } \, j = 1 , \ldots, C \\ & H_1 \colon p_{ij} \neq p_{ij}^0 \qquad \text{ for at least one pair } \, (i,j) \end{align*}

Sample:

  • We draw m items from population
  • O_{ij} denotes the number of items of type i drawn
  • Therefore O = (O_{ij})_{ij} is \mathop{\mathrm{Mult}}(m,p) with p = (p_{ij})_{ij}

Data: Matrix of counts o = (o_{ij})_{ij}

Procedure

  1. Calculation:
    • Compute total counts and expected counts m = \sum_{i=1}^R \sum_{j=1}^C o_{ij} \qquad \quad E_{ij} = m p_{ij}^0
    • Compute the chi-squared statistic \chi^2 = \sum_{i=1}^R \sum_{j=1}^C \frac{ (o_{ij} - E_{ij})^2 }{E_{ij}}

  1. Statistical Tables or R:
    • Check that E_{ij} \geq 5 for all i, j
    • No parameters fitted. By the Theorem we get {\rm degrees \,\, freedom} = RC - 1 \qquad \qquad \chi^2 \ \approx \ \chi_{RC-1}^2
    • Find critical value \chi^2_{RC - 1} (0.05) in chi-squared Table 2
    • Alternatively, compute p-value in R
  2. Interpretation: Reject H_0 when either p < 0.05 \qquad \text{ or } \qquad \chi^2 \in \,\,\text{Rejection Region}
Alternative Rejection Region p-value
\exists \, (i,j) \,\, s.t. \,\, p_{ij} \neq p_{ij}^0 \chi^2 > \chi^2_{RC-1}(0.05) P(\chi_{RC-1}^2 > \chi^2)

Goodness-of-fit test in R

  1. Store matrix of counts O = (o_{ij})_{ij} into a single R vector, proceeding row-by-row
    • counts <- c(o_11, o_12, ..., o_RC)
  2. Store matrix of null probabilities p^0 = (p_{ij}^0)_{ij} into a single R vector (row-by-row)
    • nullp.p <- c(p_11, p_12, ..., p_RC)
  3. Perform a chi-squared goodness-of-fit test on counts with null.p
Alternative R command
\exists \, (i,j) \,\, s.t. \,\, p_{ij} \neq p_{ij}^0 chisq.test(counts, p = null.p)
  1. Read output: In particular look for the p-value

Monte Carlo p-value: compute with the option simulate.p.value = T

Note: Command in 3 is exactly the same as goodness-of-fit test for simple counts

Part 2:
Worked Example

Example: Manchester United performance

Background story:

  • From 1992 to 2013 Man Utd won 13 Premier Leagues titles out of 21
  • This is the best performance (of any team) in the Premier League era
  • This was under manager Sir Alex Ferguson
  • Ferguson stepped down in 2014
  • Since 2014 Man Utd has not won the PL and was managed by 6 different people (excluding interims)

Question: Are the 6 managers to blame for worse Team Performance?

The data

Manager Won Drawn Lost
Moyes 27 9 15
Van Gaal 54 25 24
Mourinho 84 32 28
Solskjaer 91 37 40
Rangnick 11 10 8
ten Hag 61 12 28

  • Table contains Man Utd games since 2014 season (updated to 2024 season)

  • To each Man Utd game in the sample we associate two categories:

    • Manager and Result

Setting up the test

  • Question: Is the number of Wins, Draws and Losses uniformly distributed?

    • If Yes, this would suggest very poor performance

  • Hypothesis Test: To answer the question we perform a goodness-of-fit test on \begin{align*} & H_0 \colon p_{ij} = p_{ij}^0 \quad \text { for all pairs } \, (i,j) \\ & H_1 \colon p_{ij} \neq p_{ij}^0 \quad \text { for at least one pair } \, (i,j) \\ \end{align*}

  • Null Probabilities:

    • They have to model that Wins, Draws and Losses are uniformly distributed
    • To compute them, we need to compute total number of games for each manager

Computing the null probabilities

  • We compute total number of games for each manager
Manager Won Drawn Lost Total
Moyes 27 9 15 o_{1+} = 51
Van Gaal 54 25 24 o_{2+} = 103
Mourinho 84 32 28 o_{3+} = 144
Solskjaer 91 37 40 o_{4+} = 168
Rangnick 11 10 8 o_{5+} = 29
ten Hag 61 12 28 o_{6+} = 101
  • We also need the total number of games m = \sum_{i=1}^R o_{i+} = 596

Computing the null probabilities

  • The results are uniformly distributed if each manager

    • Wins (Draws, Loses) 1/3 of the games he played

  • Since Manager i plays o_{i+} games, the expected scores are E_{ij} = \frac{o_{i+}}{3} \,, \qquad j=1,2,3

  • Recall that the expected scores are modelled as E_{ij} = m p_{ij}^0

  • Thus, the null probabilities under the assumption of uniform distribution are

p_{ij}^0 = \frac13 \times \frac{o_{i+}}{m} \quad \left( = \frac{1}{3} \times \text{Proportion of total games played by Manager } \, i \right)

Computing the null probabilities

  • Substituting the values of o_{i+} and m, we obtain the null probabilities

\begin{align*} \text{Moyes: } \quad & p_{1j}^0 = \frac13 \times \frac{ o_{1+} }{ m } = 51 \big/ 1788 \\ \text{Van Gaal: }\quad & p_{2j}^0 = \frac13 \times \frac{ o_{2+} }{ m } = 103 \big/ 1788 \\ \text{Mourinho: } \quad& p_{3j}^0 = \frac13 \times \frac{ o_{3+} }{ m } = 144 \big/ 1788 \\ \text{Solskjaer: } \quad& p_{4j}^0 = \frac13 \times \frac{ o_{4+} }{ m } = 168 \big/ 1788 \\ \text{Rangnick: }\quad & p_{5j}^0 = \frac13 \times \frac{ o_{5+} }{ m } = 29 \big/ 1788 \\ \text{ten Hag: }\quad & p_{6j}^0 = \frac13 \times \frac{ o_{6+} }{ m } = 101 \big/ 1788 \end{align*}

Summary: Counts and Null probabilities


Manager Won Drawn Lost
Moyes 27 9 15
Van Gaal 54 25 24
Mourinho 84 32 28
Solskjaer 91 37 40
Rangnick 11 10 8
ten Hag 61 12 28
Manager Won Drawn Lost
Moyes \frac{51}{1788} \frac{51}{1788} \frac{51}{1788}
Van Gaal \frac{103}{1788} \frac{103}{1788} \frac{103}{1788}
Mourinho \frac{144}{1788} \frac{144}{1788} \frac{144}{1788}
Solskjaer \frac{168}{1788} \frac{168}{1788} \frac{168}{1788}
Rangnick \frac{29}{1788} \frac{29}{1788} \frac{29}{1788}
ten Hag \frac{101}{1788} \frac{101}{1788} \frac{101}{1788}

Implementation in R

  • Start by storing the matrix of counts into a single R vector, row-by-row
# Store matrix of counts into single R vector
counts <- c(27, 9, 15,
            54, 25, 24,
            84, 32, 28, 
            91, 37, 40,
            11, 10, 8,
            61, 12, 28)

  • Then we store the matrix of null probabilities into a single R vector, row-by-row
  • Null probabilities in each row are the same. Hence we can use the command rep
# Store matrix of null probabilities into single R vector
# To avoid copy pasting, first store probabilities of each Manager
manager.null.p <- c(51/1788, 103/1788, 144/1788, 
                    168/1788, 29/1788, 101/1788)

# Repeat each entry 3 times 
null.p <- rep(manager.null.p, c(3, 3, 3, 3, 3, 3))


  • Let us print the (rounded) null probabilities to aid visualization
print(round(null.p,2))     # Rounds to 2 d.p.
 [1] 0.03 0.03 0.03 0.06 0.06 0.06 0.08 0.08 0.08 0.09 0.09 0.09 0.02 0.02 0.02
[16] 0.06 0.06 0.06

  • Finally we perform the goodness-of-fit test on counts and null.p
# Perform goodness-of-fit test
ans <- chisq.test(counts, p = null.p)

# Print answer
print(ans)

Output

  • Running the code we obtain

    Chi-squared test for given probabilities

data:  counts
X-squared = 137.93, df = 17, p-value < 2.2e-16


  • p-value is p \approx 0 < 0.05
  • We therefore reject H_0
  • Significant evidence that results of Man Utd games are not uniformly distributed
  • Low goal-scoring rates in soccer mean roughly 1/3 of games end in a draw
  • Hence Man Utd is not actually doing too bad

Part 3:
Chi-squared test
of independence

Testing for independence

Owned Rented Total
North West 2180 871 3051
London 1820 1400 3220
South West 1703 614 2317
Total 5703 2885 8588

  • Consider a two-way contingency table as above

  • To each person we associate two categories:

    • Residential Status: Rental or Owned
    • Region in which they live: NW, London, SW

Testing for independence

Owned Rented Total
North West 2180 871 3051
London 1820 1400 3220
South West 1703 614 2317
Total 5703 2885 8588
  • One possible question is:
    • Does Residential Status depend on Region?
    • In other words: Are rows and columns dependent?

Testing for independence

Owned Rented Total
North West 2180 871 3051
London 1820 1400 3220
South West 1703 614 2317
Total 5703 2885 8588
  • Looking at the data, it seems clear that:
    • London: Rentals are almost comparable to Owned
    • NW and SW: Rentals are almost a third of Owned
    • It appears Residential Status and Region are dependent features
  • Goal: Formulate test for independence

Testing for independence

Y = 1 \ldots Y = C Totals
X = 1 O_{11} \ldots O_{1C} O_{1+}
\cdots \cdots \cdots \cdots \cdots
X = R O_{R1} \ldots O_{RC} O_{R+}
Totals O_{+1} \ldots O_{+C} m

  • Consider the general two-way contingency table as above

  • They are equivalent:

    • Rows and columns are independent
    • Random variables X and Y are independent

Testing for independence

Y = 1 \ldots Y = C Totals
X = 1 O_{11} \ldots O_{1C} O_{1+}
\cdots \cdots \cdots \cdots \cdots
X = R O_{R1} \ldots O_{RC} O_{R+}
Totals O_{+1} \ldots O_{+C} m

  • Hence, testing for independece means testing following hypothesis: \begin{align*} & H_0 \colon X \, \text{ and } \, Y \, \text{ are independent } \\ & H_1 \colon X \, \text{ and } \, Y \, \text{ are not independent } \end{align*}

  • We need to quantify H_0 and H_1

Testing for independence

Y = 1 \ldots Y = C Totals
X = 1 p_{11} \ldots p_{1C} p_{1+}
\cdots \cdots \cdots \cdots \cdots
X = R p_{R1} \ldots p_{RC} p_{R+}
Totals p_{+1} \ldots p_{+C} 1

  • R.v. X and Y are independent iff cell probabilities factor into marginals p_{ij} = P(X = i , Y = j) = P(X = i) P (Y = j) = p_{i+}p_{+j}

  • Therefore the hypothesis test for independence becomes \begin{align*} & H_0 \colon p_{ij} = p_{i+}p_{+j} \quad \text{ for all } \, i = 1, \ldots , R \, \text{ and } \, j = 1 ,\ldots C \\ & H_1 \colon p_{ij} \neq p_{i+}p_{+j} \quad \text{ for some } \, (i,j) \end{align*}

Expected counts

  • Assume the null hypothesis is true H_0 \colon p_{ij} = p_{i+}p_{+j} \quad \text{ for all } \, i = 1, \ldots , R \, \text{ and } \, j = 1 ,\ldots C

  • Under H_0, the expected counts become E_{ij} = m p_{ij} = p_{i+}p_{+j}

  • We need a way to estimate the marginal probabilities p_{i+} and p_{+j}

Estimating marginal probabilities

  • Goal: Estimate marginal probabilities p_{i+} and p_{+j}

  • By definition we have p_{i+} = P( X = i )

  • Hence p_{i+} is probability of and observation to be classified in i-th row

  • Estimate p_{i+} with the proportion of observations classified in i-th row p_{i+} := \frac{o_{i+}}{m} = \frac{ \text{Number of observations in } \, i\text{-th row} }{ \text{ Total number of observations} }

Estimating marginal probabilities

  • Goal: Estimate marginal probabilities p_{i+} and p_{+j}

  • Similarly, by definition p_{+j} = P( Y = j )

  • Hence p_{+j} is probability of and observation to be classified in j-th column

  • Estimate p_{+j} with the proportion of observations classified in j-th column p_{+j} := \frac{o_{+j}}{m} = \frac{ \text{Number of observations in } \, j\text{-th column} }{ \text{ Total number of observations} }

\chi^2 statistic for testing independence

  • Summary: The marginal probabilities are estimated with p_{i+} := \frac{o_{i+}}{m} \qquad \qquad p_{+j} := \frac{o_{+j}}{m}

  • Therefore the expected counts become E_{ij} = m p_{ij} = m p_{i+} p_{+j} = m \left( \frac{o_{i+}}{m} \right) \left( \frac{o_{+j}}{m} \right) = \frac{o_{i+} \, o_{+j}}{m}

  • By the Theorem in Slide 20, the chi-squared statistics satisfies \chi^2 = \sum_{i=1}^R \sum_{j=1}^C \frac{ (O_{ij} - E_{ij})^2 }{ E_{ij} } \ \approx \ \chi^2_{RC - 1 - {\rm fitted}}

  • We need to compute the number of fitted parameters

  • We estimate the first R-1 row marginals by p_{i+} := \frac{o_{i+}}{m} \,, \qquad i = 1 , \ldots, R - 1

  • Since the marginals p_{i+} sum to 1, we can obtain p_{R+} by p_{R+} = 1 - p_{1+} - \ldots - p_{(R-1)+} = 1 - \frac{o_{1+}}{m} - \ldots - \frac{o_{(R-1)+}}{m}

  • Similarly, we estimate the first C-1 column marginals by p_{+j} = \frac{o_{+j}}{m} \,, \qquad j = 1, \ldots, C - 1

  • Since the marginals p_{+j} sum to 1, we can obtain p_{+C} by p_{+C} = 1 - p_{+1} - \ldots - p_{+(C-1)} = 1 - \frac{o_{+1}}{m} - \ldots - \frac{o_{+(C-1)}}{m}

  • In total, we only have to estimate (R - 1) + (C - 1 ) = R + C - 2 parameters

  • Therefore, the fitted parameters are {\rm fitted} = R + C - 2

  • Consequently, the degrees of freedom are \begin{align*} RC - 1 - {\rm fitted} & = RC - 1 - R - C + 2 \\ & = RC - R - C + 1 \\ & = (R - 1)(C - 1) \end{align*}

\chi^2 statistic for testing independence

Conclusion

  • Assume the null hypothesis of row and column independence H_0 \colon p_{ij} = p_{i+}p_{+j} \quad \text{ for all } \, i = 1, \ldots , R \, \text{ and } \, j = 1 ,\ldots C

  • Suppose the counts are O \sim \mathop{\mathrm{Mult}}(m,p), and expected counts are E_{ij} = \frac{o_{i+} \, o_{+j}}{m}

  • By the previous slides, and Theorem in Slide 20 we have that \chi^2 = \sum_{i=1}^R \sum_{j=1}^C \frac{ (O_{ij} - E_{ij})^2 }{ E_{ij} } \approx \ \chi_{RC - 1 - {\rm fitted} }^2 = \chi_{(R-1)(C-1)}^2

\chi^2 statistic for testing independence

Quality of approximation

The chi-squared approximation \chi^2 = \sum_{i=1}^R \sum_{j=1}^C \frac{ (O_{ij} - E_{ij})^2 }{ E_{ij} } \approx \ \chi_{(R-1)(C-1)}^2 is good if E_{ij} \geq 5 \quad \text{ for all } \,\, i = 1 , \ldots , R \, \text{ and } j = 1, \ldots, C

The chi-squared test of independence

Sample:

  • We draw m individuals from population

  • Each individual can be of type (i,j), where

    • i = 1 , \ldots ,R
    • j = 1 , \ldots ,C
    • Total of n = RC types

  • O_{ij} denotes the number of items of type (i,j) drawn

  • p_{ij} is probability of observing type (i,j)

  • p = (p_{ij})_{ij} is probability matrix

  • The matrix of counts O = (o_{ij})_{ij} has multinomial distribution \mathop{\mathrm{Mult}}(m,p)

Data: Matrix of counts, represented by two-way contigency table

Y = 1 \ldots Y = C Totals
X = 1 o_{11} \ldots o_{1C} o_{1+}
\cdots \cdots \cdots \cdots \cdots
X = R o_{R1} \ldots o_{RC} o_{R+}
Totals o_{+1} \ldots o_{+C} m

Hypothesis test: We test for independence of rows and columns \begin{align*} & H_0 \colon X \, \text{ and } \, Y \, \text{ are independent } \\ & H_1 \colon X \, \text{ and } \, Y \, \text{ are not independent } \end{align*}

Procedure: 3 Steps

  1. Calculation:

    • Compute marginal and total counts o_{i+} := \sum_{j=1}^C o_{ij} \,, \qquad o_{+j} := \sum_{i=1}^R o_{ij} \,, \qquad m = \sum_{i=1}^R o_{i+} = \sum_{j=1}^C o_{+j}

    • Compute the expected counts E_{ij} = \frac{o_{i+} \, o_{+j} }{ m }

    • Compute the chi-squared statistic \chi^2 = \sum_{i=1}^R \sum_{j=1}^C \frac{ (o_{ij} - E_{ij})^2 }{E_{ij}}

  1. Statistical Tables or R:
    • Check that E_{ij} \geq 5 for all i and j
    • We fitted R + C - 2 parameters. By the Theorem we get \chi^2 \ \approx \ \chi_{\rm df}^2 \,, \qquad {\rm df} = {\rm degrees \,\, freedom} = (R-1)(C-1)
    • Find critical value \chi^2_{\rm df} (0.05) in chi-squared Table 2
    • Alternatively, compute p-value in R
  2. Interpretation: Reject H_0 when either p < 0.05 \qquad \text{ or } \qquad \chi^2 \in \,\,\text{Rejection Region}
Alternative Rejection Region p-value
X and Y not independent \chi^2 > \chi^2_{\rm{df}}(0.05) P(\chi_{\rm df}^2 > \chi^2)

The chi-squared test of independence in R

  1. Store each row of counts (o_{i1}, o_{i2}, \ldots, o_{iC}) in R vector
    • row_i <- c(o_i1, o_i2, ..., o_iC)
  2. The matrix of counts o = (o_{ij})_{ij} is obtained by assembling rows into a matrix
    • counts <- rbind(row_1, ..., row_R)
  3. Perform a chi-squared goodness-of-fit test on counts with null.p
Alternative R command
X and Y are independent chisq.test(counts)
  1. Read output: In particular look for the p-value

Note: Compute Monte Carlo p-value with option simulate.p.value = TRUE

Part 4:
Worked Example

Example: Residential Status and Region

Owned Rented Total
North West 2180 871 3051
London 1820 1400 3220
South West 1703 614 2317
Total 5703 2885 8588

  • People are sampled at random in NW, London and SW

  • To each person we associate two categories:

    • Residential Status: Rental or Owned
    • Region in which they live: NW, London, SW

  • Question: Are Residential Status and Region independent?

Chi-squared test of independence by hand

  1. Calculation:
    • Total and marginal counts are already provided in the table
Owned Rented Tot
NW 2180 871 o_{1+} = 3051
Lon 1820 1400 o_{2+} = 3220
SW 1703 614 o_{2+} = 2317
Tot o_{+1} = 5703 o_{+2} = 2885 m = 8588

  • Compute the estimated expected counts E_{ij} = \dfrac{o_{i+} \, o_{+j} }{ m }
Owned Rented Tot
NW \frac{3051{\times}5703}{8588} \approx 2026 \frac{3051{\times}2885}{8588} \approx 1025 o_{1+} = 3051
Lon \frac{3220{\times}5703}{8588} \approx 2138 \frac{3220{\times}2885}{8588} \approx 1082 o_{2+} = 3220
SW \frac{2317{\times}5703}{8588} \approx 1539 \frac{2317{\times}1885}{8588} \approx 778 o_{2+} = 2317
Tot o_{+1} = 5703 o_{+2} = 2885 m = 8588

  • Compute the chi-squared statistic \begin{align*} \chi^2 & = \sum_{i=1}^R \sum_{j=1}^C \frac{ (o_{ij} - E_{ij})^2 }{E_{ij}} \\ & = \frac{(2180-2026.066)^2}{2026.066} + \frac{(871-1024.934)^2}{1024.934} \\ & \, + \frac{(1820-2138.293)^2}{2138.293}+\frac{(1400-1081.707)^2}{1081.707} \\ & \, + \frac{(1703-1538.641)^2}{1538.641}+\frac{(614-778.359)^2}{778.359} \\ & = 11.695+23.119 \\ & \, + 47.379+93.658 \\ & \, + 17.557+34.707 \\ & = 228.12 \qquad (2\ \text{d.p.}) \end{align*}

  1. Statistical Tables:
    • Rows are R = 3 and columns are C = 2
    • Degrees of freedom are \, {\rm df} = (R - 1)(C - 1) = 2
    • We clearly have E_{ij} \geq 5 for all i and j
    • Therefore, the following approximation holds \chi^2 \ \approx \ \chi_{(R - 1)(C - 1)}^2 = \chi_{2}^2
    • In chi-squared Table 2, we find critical value \chi^2_{2} (0.05) = 5.99

  1. Interpretation:
    • We have that \chi^2 = 228.12 > 5.99 = \chi_{2}^2 (0.05)
    • Therefore we rejct H_0, meaning that rows and columns are dependent
  • There is evidence (p < 0.05) that Residential Status depends on Region
  • By rescaling table values, we can compute the table of percentages
Owned Rented
North West 71.5\% 28.5\%
London 56.5\% 43.5\%
South West 73.5\% 26.5\%
  • The above suggests that in London fewer homes are Owned and more Rented

Chi-squared test of independence in R

# Store each row into and R vector
row_1 <- c(2180, 871)
row_2 <- c(1820, 1400)
row_3 <- c(1703, 614)

# Assemble the rows into an R matrix
counts <- rbind(row_1, row_2, row_3)

# Perform chi-squared test of independence
ans <- chisq.test(counts)

# Print answer
print(ans)

Output

  • Running the code, we obtain

    Pearson's Chi-squared test

data:  counts
X-squared = 228.11, df = 2, p-value < 2.2e-16


  • This confirms the chi-squared statistic computed by hand \chi^2 = 228.11
  • It also confirms the degrees of freedom \, {\rm df} = 2
  • The p-value is p \approx 0 < 0.05
  • Therefore H_0 is rejected, and Residential Status depends on Region

Exercise: Manchester United performance

Manager Won Drawn Lost
Moyes 27 9 15
Van Gaal 54 25 24
Mourinho 84 32 28
Solskjaer 91 37 40
Rangnick 11 10 8
ten Hag 61 12 28

  • Table contains Man Utd games since 2014 season (updated to 2024)

  • To each Man Utd game in the sample we associate two categories:

    • Manager and Result

  • Question: Is there association between Manager and Team Performance?

Solution

  • To answer the question, we perform chi-squared test of independence in R

  • Test can be performed by suitably modifying the code independence_test.R

# Store each row into and R vector
row_1 <- c(27, 9, 15)
row_2 <- c(54, 25, 24) 
row_3 <- c(84, 32, 28) 
row_4 <- c(91, 37, 40)
row_5 <- c(11, 10, 8)
row_6 <- c(61, 12, 28)

# Assemble the rows into an R matrix
counts <- rbind(row_1, row_2, row_3, row_4, row_5, row_6)

# Perform chi-squared test of independence
ans <- chisq.test(counts)

# Print answer
print(ans)

Output

  • Running the code we obtain

    Pearson's Chi-squared test

data:  counts
X-squared = 12.678, df = 10, p-value = 0.2422


  • p-value is p \approx 0.24 > 0.05
  • We do not reject H_0
  • There is no evidence of association between Manager and Team Performance
  • This suggests that changing the manager alone will not resolve poor performance

Part 5:
Monte Carlo
simulations

For simple counts, we said that:

  • The distribution of the \chi^2 statistic is approximately \chi^2 = \sum_{i=1}^n \frac{(O_i - E_i)^2 }{ E_i } \ \approx \ \chi_{n-1}^2

  • The approximation is:

    Good E_i \geq 5 \, \text{ for all } \, i = 1 , \ldots n
    Bad E_i < 5 \, for some \, i = 1 , \ldots n

  • How to compute the p-value: When approximation is

    • Good: Use \chi_{n-1}^2 approximation of \chi^2
    • Bad: Use Monte Carlo simulations

  • Question: What is a Monte Carlo simulation?

Monte Carlo methods

  • Monte Carlo methods:
    • Broad class of computational algorithms
    • They rely on repeated random sampling to obtain numerical results
    • Principle: use randomness to solve problems which are deterministic
  • Why the name?
    • Method was developed by Stanislaw Ulam
    • His uncle liked to gamble in the Monte–Carlo Casino in Monaco
  • Examples of applications:
    • First used to solve problem of neutron diffusion in Los Alamos 1946
    • Can be used to compute integrals
    • Can be used to compute p-values

Example: Approximation of \pi

  • Throw random points inside square of side 2
  • Count proportion of points falling inside unit circle
  • Such proportion approximates \pi (area of the circle)
    • r = \, Red point
    • b = \, Blue point
    • n = r + b Total points

\frac{\pi}{4} \approx \frac{r}{n} \,\, \implies \,\, \pi \approx \frac{4r}{n}

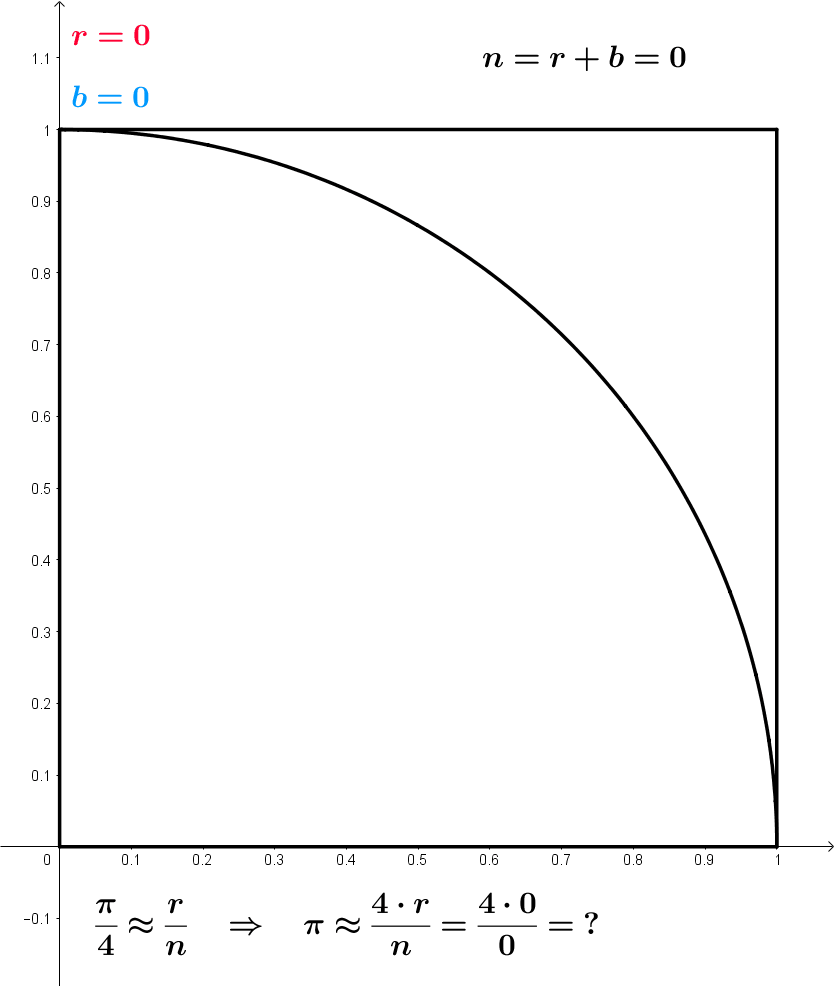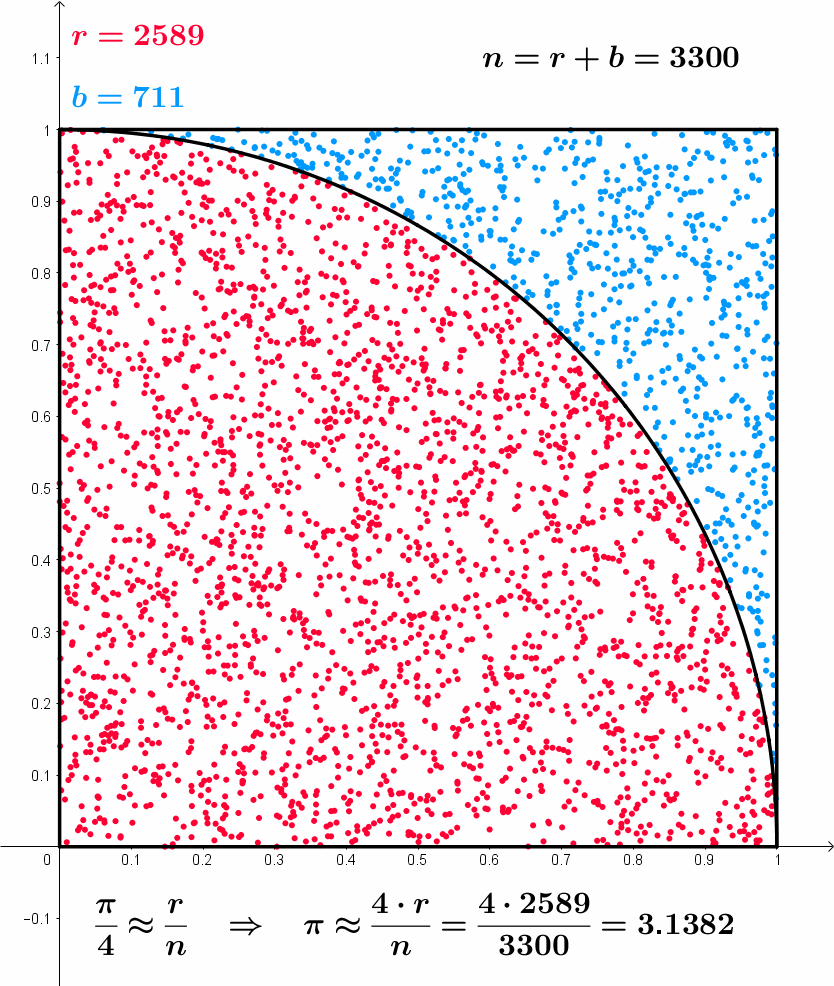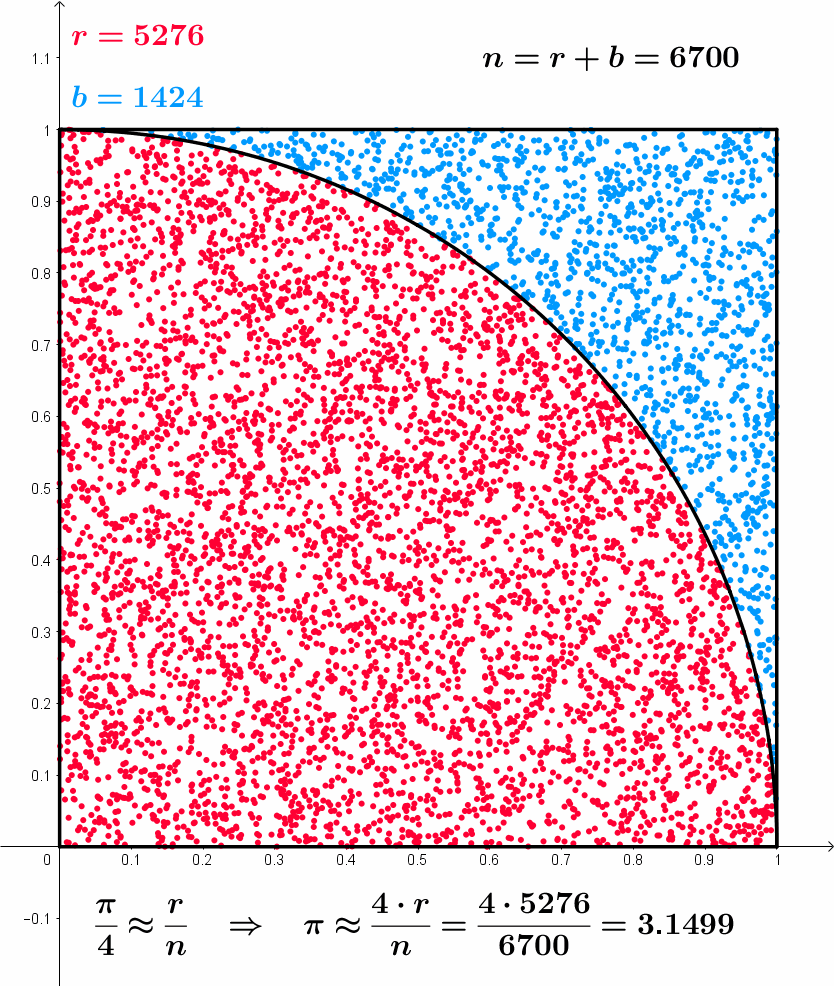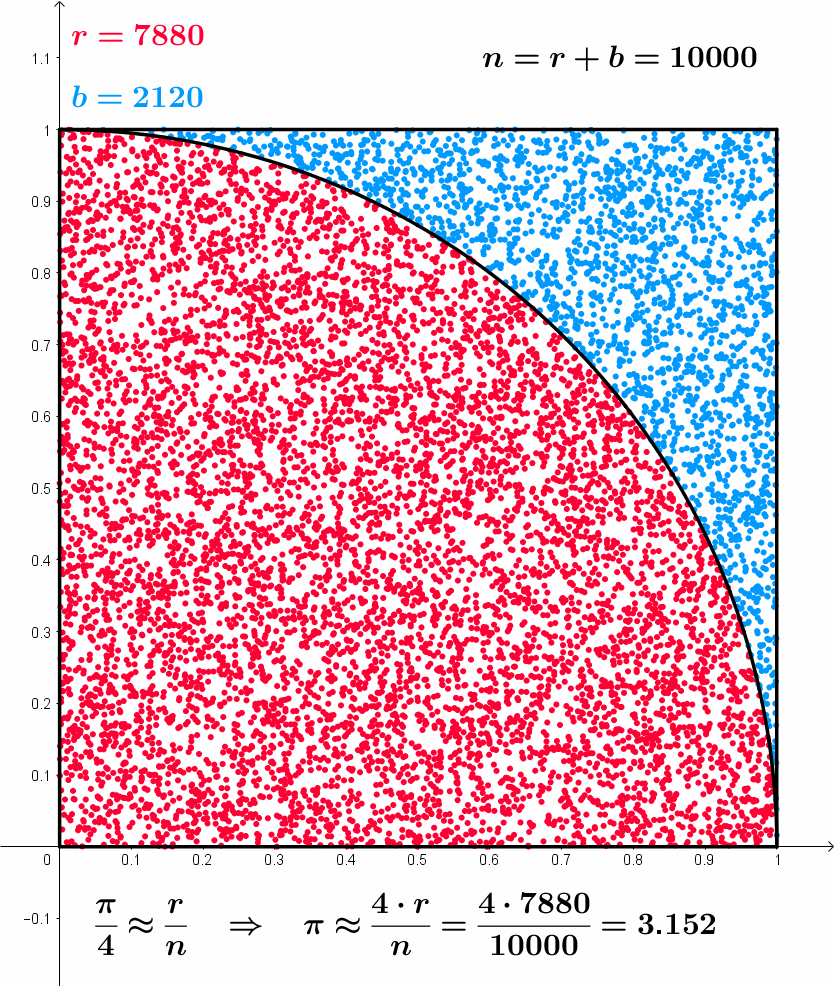
Approximating \pi – Formal model

  • Draw x_1, \ldots, x_N and y_1, \ldots, y_N from {\rm Uniform(-1,1)}

  • Count the number of points (x_i,y_i) falling inside circle of radius 1

  • These are points satisfying condition x_i^2 + y_i^2 \leq 1

  • Area of circle estimated with proportion of points falling inside circle: \text{Area} \ = \ \pi \ \approx \ \frac{\text{Number of points } (x_i,y_i) \text{ inside circle}}{N} \ \times \ 4

  • Note: 4 is the area of square of side 2

Plot: 1000 random points in square of side 2

Approximation of \pi in R

N <- 10000      # We do 100000 iterations and print every 10000
total <- 0      # Counts total number of points
in_circle <- 0  # Counts points falling in circle

for (j in 1:10) {   # This loop is for printing message every N iterations
  for (i in 1:N) {  # Loop in which points are counted
    x <- runif(1, -1, 1); y <- runif(1, -1, 1);  # sample point (x,y)
    if (x^2 + y^2 <= 1) {    
      in_circle <- in_circle + 1  # If (x,y) in circle increase counter
    }
    total <- total + 1  # Increase total counter (in any case)
  }
  
  pi_approx <- ( in_circle / total ) * 4  # Compute approximate area

  cat(sprintf("After %8d iterations pi is %.08f, error is %.08f\n",
     (j * N), pi_approx, abs(pi_approx - pi)))
}

Approximation of \pi in R: Output

After    10000 iterations pi is 3.13600000, error is 0.00559265
After    20000 iterations pi is 3.13280000, error is 0.00879265
After    30000 iterations pi is 3.14480000, error is 0.00320735
After    40000 iterations pi is 3.14700000, error is 0.00540735
After    50000 iterations pi is 3.14280000, error is 0.00120735
After    60000 iterations pi is 3.14080000, error is 0.00079265
After    70000 iterations pi is 3.14405714, error is 0.00246449
After    80000 iterations pi is 3.14530000, error is 0.00370735
After    90000 iterations pi is 3.14217778, error is 0.00058512
After   100000 iterations pi is 3.14212000, error is 0.00052735

Note:

  • The error decreases overall, but there are random fluctuations

  • This is because we are trying to approximate \pi by a random quantity

A word on error estimates

  • Deriving error estimates for numerical methods is not easy (Numerical Analysis)

  • Going back to our example:

    • Let n denote the total number of points drawn
    • Let X_n denote the proportion of points falling inside the unit circle

  • For every \varepsilon> 0 fixed, it can be shown that P( | X_n - \pi/4 | \geq \varepsilon) \leq {\rm Error} = \frac{1}{20 n \varepsilon^2}

  • To get small Error: \,\, \varepsilon has to be small, n has to be large

    • Fixing a small error threshold \varepsilon implies doing more iterations (larger n)
    • Error estimate is probabilistic: Error fluctuates, but decreases with more iterations

  • Estimate can be derived by interpreting the problem as the Monte Carlo integration of \int_0^1 \sqrt{1-x^2} \, dx = \pi /4, see stackexchange post

Simulation: The main point (for us)

Simulation can be used to gain insight into the shape of a distribution:

  • Mean and variance

  • Related probabilities (p-values)

How to simulate in R:

  • Use loops
    • Example: We used a for loop to simulate \pi
  • Use ad hoc R commands
    • replicate(n, expr) repeats expression n times and outputs results
    • apply(x, expr) applies expression to the object x

Example: Estimating mean / variance of \overline{X}

Consider sample X_1, \ldots, X_n from N(\mu,\sigma^2)

  • Recall that the sample mean satisfies {\rm I\kern-.3em E}[\overline{X}] = \mu \,, \qquad {\rm Var}[\overline{X}] = \frac{\sigma^2}{n} (As n gets larger, {\rm Var}[\overline{X}] will be closer to 0 \implies \overline{X} \approx \mu when n is large)

  • For example, if the sample size is n = 10, mean \mu = 0 and sd \sigma = 1, then {\rm I\kern-.3em E}[\overline{X}] = 0 \,, \qquad {\rm Var}[\overline{X}] = \frac{1}{10} = 0.1

  • We can obtain the above quantitites through simulation
    (In fancy terms: Estimating mean and variance of \overline{X})

  • One simulation of \overline{X} can be done as follows:
    1. Generate sample x_1, \ldots, x_n from N(0,1)
    2. Compute sample mean of x_1, \ldots, x_n
# Simulate the sample mean xbar

n <- 10
sim.xbar <- mean(rnorm(n))
  • To simulate M = 1000 values from \overline{X}, replicate the above command M times
# Simulate M = 1000 times the sample mean xbar
n <- 10; M <- 1000

sim.xbar <- replicate(M, mean(rnorm(n)))

  • The vector sim.xbar contains M=1000 simulations from \overline{X}

  • Reasonable to suppose that sim.xbar approximates the random variable \overline{X}
    (This can be made rigorous with Central Limit Thm)

  • Therefore, we can make the following estimation

Quantity Estimation
{\rm I\kern-.3em E}[\overline{X}] Sample mean of sim.xbar
{\rm Var}[\overline{X}] Sample variance of sim.xbar 


# Print mean and variance of sample mean
cat("Expected value:", mean(sim.xbar), "Variance:", var(sim.xbar))
Expected value: 0.005180686   Variance: 0.1058328


These are very close to the theoretical values: \quad {\rm I\kern-.3em E}[\overline{X}] = 0 \,, \quad {\rm Var}[\overline{X}] = \frac{1}{10} = 0.1

Example: Sample mean VS sample median

  • Both sample mean and median can be used to estimate the center of a distribution

  • But which one is better?

  • Suppose the population is N(\mu,\sigma^2)

  • We know that the sample mean \overline{X} satisfies {\rm I\kern-.3em E}[\overline{X}] = \mu \,, \qquad {\rm Var}[\overline{X}] = \frac{\sigma^2}{n}

  • However, no such formulas are available for the sample meadian

Question: How can we compare them? Use simulation

To simulate sample mean and median from N(0,1), we do:

  • Generate sample x_1, \ldots, x_{10} from N(0,1), and compute sample mean and median

  • Repeat M = 1000 times

M <- 1000; n <- 10  
sim.mean <- replicate(M, mean(rnorm(n)))
sim.median <- replicate(M, median(rnorm(n)))

  • To compare simulated sample mean and median, we can produce a boxplot

  • The one with smallest variance, will be the better estimator for the true population mean \mu = 0

boxplot(list("sample mean" = sim.mean, 
             "sample median" = sim.median),
        main = "Normal population N(0,1)")

  • The sample mean has less variability
  • It is the preferred estimator for the true population mean
    (when the population is normal)

Example: Computing probabilities

Question: What is the probability of rolling 7 with two dice?

  • Of course this problem has combinatorial answer: p = \frac16

  • But we can also answer using simulation

  • To simulate the roll of a dice, we use the function sample

    • sample(x, n, replace = T)
    • samples n times from vector x with replacement

  • To roll 2 dice, we input:

# Roll two dice

sample(1:6, 2, replace = T)
[1] 3 1

To compute the probability of rolling 7 with two dice we do:

  • Simulate one roll of the two dice, and sum the outcome
  • Repeat M = 1000 times
  • Estimate the probability of rolling a 7 with P(\text{Rolling } 7) \approx \frac{\# \text{ of times the simulated roll is } 7 }{1000} 
M <- 1000

sim.rolls <- replicate(M, sum( sample(1:6, 2, replace = T) ))

number.of.7s <- sum( sim.rolls == 7 )
p <- number.of.7s / M

cat("The estimated probability of rolling 7 is", p)
The estimated probability of rolling 7 is 0.166
  • This is very close to the theoretical probability p = 1/6

Example: Interpretation of Confidence Intervals

  • Suppose given a normal population N(\mu,\sigma^2)

  • A 95 \% confidence interval for the true mean \mu is a (random) interval [a,b] s.t. P(\mu \in [a,b]) = 0.95

  • Confidence interval is not probability statement about \mu – note \mu is a constant!

  • It is probability statement about [a,b]

Interpretation: The random interval [a,b] contains the mean \mu with probability 0.95

Constructing the confidence interval with t-statistic:

  • Suppose given a sample x_1, \ldots, x_n from N(\mu,\sigma^2)

  • Recall: the t-statistic has t-distribution t = \frac{\overline{x}-\mu}{\mathop{\mathrm{e.s.e.}}} \, \sim \, t_{n-1} \,, \qquad \mathop{\mathrm{e.s.e.}}= \frac{s}{\sqrt{n}}

  • We impose that t is observed with probability 0.95 P(- t^* \leq t \leq t^*) = 0.95 \,, \qquad t^* = t_{n-1}(0.025)

  • The 95\% confidence interval is obtained by solving above equation for \mu P(\mu \in [a,b] ) = 0.95 \,, \qquad a = \overline{x} - t^* \times \mathop{\mathrm{e.s.e.}}, \qquad b = \overline{x} + t^* \times \mathop{\mathrm{e.s.e.}}

  • Interpretation: If you sample over and over again, the interval [a,b] will contain \mu about 95\% of the times

  • Each row of points is a sample from the same normal distribution \qquad (Image from Wikipedia)

  • The colored lines are confidence intervals for the mean \mu

  • At the center of each interval is the sample mean (diamond)

  • The blue intervals contain the population mean, and the red ones do not

Simulating one confidence interval in R:

  • Sample n = 100 times from N(0,1)
    • Running a t-test on the sample gives a confidence interval for the unknown mean \mu
    • The confidence interval can be retrieved with $conf.int
# Sample 100 times from N(0,1)
x <- rnorm(100)

# Compute confidence interval using t.test
interval <- t.test(x)$conf.int
  • interval is a vector containing the simulated confidence interval
    • Left extreme in interval[1] \qquad Right extreme in interval[2]
a <- interval[1];   b <- interval[2]

cat("Simulated confidence interval: a =", a, "  b = ", b)
Simulated confidence interval: a = -0.2262375   b =  0.1689576
  • In this case the interval contains the true mean \mu = 0

Testing the claim: \quad P (\mu \in [a,b]) = 0.95

  • If you sample over and over, the interval [a,b] will contain \mu about 95\% of the times

We test with the following method:

  • Sample n = 100 times from N(0,1) and compute confidence interval

  • Repeat M = 1000 times

  • Check how many times \mu = 0 belongs to simulated confidence intervals

  • Estimate the probability of the CI containing \mu as P(\mu \in [a,b]) \approx \frac{\# \text{ of times } \mu = 0 \text{ belongs to simulated } [a,b]}{M}

  • The estimate should approach 0.95

  • First, we simulate the M = 1000 confidence intervals
# Simulate M confidence intervals for the mean
n <- 100; M <- 10000

intervals <- replicate(M, t.test(rnorm(n)) $ conf.int)
  • intervals is a matrix containing the M = 1000 simulated intervals (as columns)
    • Left extremes are in intervals[1, ]
    • Right extremes are in intervals[2, ]
  • For visualization, we print the first 5 confidence intervals
# Print the first 5 columns of intervals
intervals[ ,1:5]
           [,1]        [,2]       [,3]       [,4]        [,5]
[1,] -0.2262375 -0.07222545 -0.2428610 -0.1788659 -0.07420973
[2,]  0.1689576  0.35116698  0.1201007  0.2189942  0.30661995

  • Now, we have our M = 1000 confidence intervals for \mu = 0

  • Check how many times \mu = 0 belongs to simulated confidence intervals

# Save left and right extremes in vectors
a <- intervals[1, ];   b <- intervals[2, ]

# Check how many times mu = 0 belongs to (a,b)
mu.belongs <- sum( (a < 0) & (0 < b) )

# Estimate the probability that mu = 0 belongs to (a,b)
p <- mu.belongs / M

cat("mu = 0 belongs to the confidence interval with probability", p)
mu = 0 belongs to the confidence interval with probability 0.9494
  • This approximates the theoretical probability P(\mu \in [a,b]) = 0.95 (we would need more confidence intervals for a better estimate)

Part 6:
Simulating p-values

The problem of simulating p-values

Suppose given a random variable X such that

  • The distribution of X is (possibly) unknown

  • A method for simulating X is available

    • This means we can (somehow) sample values from X

Goal: For a given x^*, we want to estimate the p-value

p = P(X > x^*)

General recipe to simulate p-values

Goal: Estimate the p-value p = P(X>x^*)

  1. Simuate the random varible X. You obtain a numerical value X_{\rm sim}

  2. The simulated value is extreme if X_{\rm sim} > x^*

  3. There are two possibilities:

    • X_{\rm sim} is extreme \quad \,\,\, \quad \implies \quad simulation goes in favor of \, p
    • X_{\rm sim} is not extreme \quad \implies \quad simulation goes in favor of \, 1-p

  4. We estimate the p-value as p = P( X > x^* ) \ \approx \ \frac{ \# \text{ of extreme simulated values} }{ \text{Total number of simulations} }

Example: Monte Carlo p-value for goodness-of-fit test

Goal: use Monte Carlo simulations to compute p-value for goodness-of-fit test

  • Consider data counts
Type 1 \ldots n Total
Observed counts o_1 \ldots o_n m
Null Probabilities p_1^0 \ldots p_n^0 1

  • The expected counts are E_i = m p_i^0

  • Under the null hypothesis, the observed counts (o_1, \ldots, o_n) come from (O_1 , \ldots, O_n) \sim \mathop{\mathrm{Mult}}(m, p_1^0, \ldots, p_n^0)

p-value for goodness-of-fit test

  • The chi-squared statistic random variable is \chi^2 = \sum_{i=1}^n \frac{(O_i - E_i)^2 }{ E_i }

  • The observed chi-squared statistics is \chi^2_{\rm obs} = \sum_{i=1}^n \frac{(o_i - E_i)^2 }{ E_i }

  • The p-value is defined as p = P( \chi^2 > \chi^2_{\rm obs} )

Problem: Computing p-value for low counts

  • Suppose E_i < 5 for some i

  • In this case, \chi^2 is not \chi^2_{n-1} distributed

  • In fact, the distribution is unknown \chi^2 = \sum_{i=1}^n \frac{(O_i - E_i)^2 }{ E_i } \ \, \sim \ \, ???

  • If the distribution is unknown, how do we compute the p-value p = P( \chi^2 > \chi^2_{\rm obs} ) \ \ ???

Exercise: Come up with a simulation to approximate p

Method: Simulating p-value for \chi^2 statistic

  1. Simulate counts (o_1^{\rm sim},\ldots,o_n^{\rm sim}) from \mathop{\mathrm{Mult}}(m, p_1^0, \ldots, p_n^0)

  2. Compute the corresponding simulated chi-squared statistic \chi^2_{\rm sim} = \sum_{i=1}^n \frac{ (o_i^{\rm sim} - E_i)^2 }{E_i} \,, \qquad E_i := m p_i^0

  3. The simulated chi-squared statistic is extreme if \chi^2_{\rm sim} > \chi^2_{\rm obs} \,, \quad \text{ where \, } \chi^2_{\rm obs} = \sum_{i=1}^n \frac{(o_i - E_i)^2 }{ E_i } \,, \,\, o_i \, \text{ the observed counts}

  4. We estimate the theoretical p-value by p = P( \chi^2 > \chi^2_{\rm obs} ) \ \approx \ \frac{ \# \text{ of extreme simulated statistics} }{ \text{Total number of simulations} }

Exercise

Data: Number of defects in printed circuit boards, along with null probabilities

# Defects 0 1 2 3
Counts 32 15 9 4
Null Probabilities 0.5 0.3 0.15 0.05
  • Total number of counts is m = 60. Expected counts are E_i = m p_i^0
E_1 E_2 E_3 E_4
30 18 9 3

  • Note: E_4 = 3 < 5 \quad \implies \quad the distribution of \chi^2 is unknown

  • Exercise: Write R code to perform a goodness-of-fit test on above data

    • You may not use the function chisq.test
    • p-value should be simulated (see previous slide)

Solution

  • First, compute the observed chi-squared statistic:
    • Enter observed counts and null probabilities
    • Compute total counts, expected counts and \chi^2_{\rm obs}
# Enter counts and null hypothesis probabilities
counts <- c(32, 15, 9, 4)
null.p <- c(0.5, 0.3, 0.15, 0.05)

# Compute total counts
m <- sum(counts)

# Compute expected counts
exp.counts <- m * null.p

# Compute the observed chi-squared statistic
obs.chi <- sum( (counts - exp.counts)^2 / exp.counts )

We now generate M = 10000 simulated chi-squared statistics:

  1. Simulate counts (o_1^{\rm sim},\ldots,o_n^{\rm sim}) from \mathop{\mathrm{Mult}}(m, p_1^0, \ldots, p_n^0)

  2. Compute the corresponding simulated chi-squared statistic \chi^2_{\rm sim} = \sum_{i=1}^n \frac{ (o_i^{\rm sim} - E_i)^2 }{E_i} 

# Simulate M chi-squared statistics
M <- 10000

sim.chi <- replicate(M, {
                # Simulate multinomial counts under null hypothesis
                sim.counts <- rmultinom(1, m, null.p)
                            
                # Reurn chi-squared statistic from the simulated counts
                sum( (sim.counts - exp.counts )^2 / exp.counts)
                })

  • The vector sim.chi contains M = 10000 simulated chi-squared statistics

  • We approximate the p-value by p = P(\chi^2 > \chi_{\rm obs}^2) \approx \ \frac{ \# \text{ of extreme simulated statistics} }{ M } 

# Check how many simulated statistics are extreme
num.extreme <- sum( sim.chi > obs.chi )

# Estimate the p-value
sim.p.value <- num.extreme / M

  • As cross check, we also simulate the p-value with chisq.test
# Perform chi-squared test using built-in R function
ans <- chisq.test(counts, p = null.p, simulate.p.value = T)

# Extract p-value from chi-squared test result
R.p.value <- ans$p.value

# Print p-values for comparison
cat("\nOur simulated p-value is:", sim.p.value)
cat("\nR simulated p-value is:", R.p.value)

Our simulated p-value is: 0.8169

R simulated p-value is: 0.8195902


  • Note: The simulated p-values are the same! (up to random fluctuations)

  • Conclusion: We see that p > 0.05. There is not enogh evidence to reject H_0

Homepage      License      Contact