Statistical Models

Lecture 3

Dr. Silvio Fanzon
S.Fanzon@hull.ac.uk

University of Hull

Lecture 3:
The t-test and
an introduction to R

Outline of Lecture 3

  1. Hypothesis testing
  2. The t-test by hand
  3. The basics of R
  4. Vectors
  5. The t-test in R
  6. Graphics
  7. Functions
  8. More on Vectors

Part 1:
Hypothesis testing

Definition of Hypothesis

  • Idea:
    • Interested in knowing a population parameter \theta
    • \theta cannot be measured directly
    • We can sample the population and draw conclusions on \theta
    • Such conclusions are called hypotheses

Definition
A hypothesis is a statement about a population parameter

Complementary hypotheses

  • Two hypotheses are complementary if exactly one of them can be true

  • Complementary hypotheses are called:

    • H_0 the null hypothesis
    • H_1 the alternative hypothesis

  • Goal: Find a way to decide which between H_0 and H_1 is true

How to model hypotheses

We denote by:

  • \theta a population parameter
  • \Theta the space of all population parameters

For \Theta_0 \subset \Theta we define the associated null and alternative hypotheses as \begin{align*} H_0 \colon & \theta \in \Theta_0 & \qquad \text{ null hypothesis} \\ H_1 \colon & \theta \in \Theta_0^c & \qquad \text{ alternative hypothesis} \end{align*}

Definition of Hypothesis test

Definition

A hypothesis test is a rule to decide:

  • For which sample values we decide to accept H_0 as true
  • For which sample values we reject H_0 and accept H_1 as true

Acceptance and Critical regions

The sample space is partitioned into two regions:

  • Acceptance region: For samples \mathbf{x} in this region we accept H_0
  • Critical region: For samples \mathbf{x} in this region we reject H_0

In most cases: Critical region is defined in terms of a test statistic W(\mathbf{x})

Example: We could decide to reject H_0 if W(\mathbf{x}) \in R with R \subset \mathbb{R} some rejection region

One-sided vs Two-sided Tests

Let \theta be one dimensional parameter. A hypothesis test is:

  • One-sided: if the null and alternative hypotheses are of the form H_0 \colon \theta \leq \theta_0 \,, \qquad H_1 \colon \theta > \theta_0 or also H_0 \colon \theta \geq \theta_0 \,, \qquad H_1 \colon \theta < \theta_0

  • Two-sided: if the null and alternative hypotheses are of the form H_0 \colon \theta = \theta_0 \,, \qquad H_1 \colon \theta \neq \theta_0

Example 1: Two-sided test

We want to assess whether a coin is fair

  • To test fairness, toss the coin many times and record outcome

  • \theta = proportion of Heads

  • The decision is between:

    • Null hypothesis: The coin is fair \,\, \implies \,\, \theta = \frac12
    • Alternative hypothesis: The coin is not fair \,\, \implies \,\, \theta \neq \frac12

Hypothesis test: \qquad \quad H_0 \colon \theta = \frac12 \,, \qquad H_1 \colon \theta \neq \frac12

Example 2: One-sided test

A University wants to advertise its MBA Program: \text{ MBA } = \text{ higher salary }

  • Is this a true or false statement?

  • The University has only access to incomplete data (could not ask all former students). Need hypothesis testing

  • \theta = average change in salary after completing the MBA program

    • Null hypothesis: No improvement in salary \,\, \implies \,\, \theta \leq 0
    • Alternative hypothesis: Salary increases \,\, \implies \,\, \theta > 0

Hypothesis test: \qquad \quad H_0 \colon \theta \leq 0 \,, \qquad H_1 \colon \theta > 0

Part 2:
The t-test by hand

One-sample Two-sided t-test

Goal: estimate the mean \mu of a normal population N(\mu,\sigma^2). If \mu_0 is guess for \mu H_0 \colon \mu = \mu_0 \qquad H_1 \colon \mu \neq \mu_0

  • One-sample means we sample only from one population
  • The variance \sigma is unknown
  • Suppose the sample size is n, with sample X_1 ,\ldots,X_n
  • We consider the t-statistics T = \frac{\overline{X}-\mu_0}{S/\sqrt{n}}
  • Recall: T \sim t_{n-1} Student’s t-distribution with n-1 degrees of freedom

Procedure for all tests

  1. Calculation
  2. Reference statistical tables or numerical values
  3. Interpretation

One-sample Two-sided t-test

Calculation

  • We have n samples available x_1,\ldots,x_n
  • Compute sample mean \overline{x} = \frac{1}{n} \sum_{i=1}^n x_i
  • Compute the sample standard deviation s = \sqrt{\frac{\sum_{i=1}^n x_i^2 - n \overline{x}^2}{n-1}}

One-sample Two-sided t-test

Calculation

  • Compute the estimated standard error \mathop{\mathrm{e.s.e.}}= \frac{s}{\sqrt{n}}

  • Compute the sample t-statistic t = \frac{\text{estimate } - \text{ hypothesised value}}{\mathop{\mathrm{e.s.e.}}} = \frac{\overline x - \mu_0}{s/\sqrt{n}}

  • \mu_0 is the value of the null hypothesis H_0

One-sample Two-sided t-test

p-value

  • After computing t-statistic, we need to compute the p-value

  • p-value is a measure of likely we are to observe the data if we assume the null hypothesis is true

  • We have 2 options:

    • LOW p-value \quad \implies \quad reject H_0
    • HIGH p-value \quad \implies \quad do not reject H_0

  • In this module we reject H_0 for p-values p<0.05

One-sample Two-sided t-test

p-value

  • For the two-sided t-test, the p-value is defined as p := 2P(t_{n-1} > |t| \, | \, H_0) where t_{n-1} follows the t-distribution with n-1 degrees of freedom

  • In other words, the p-value is p = 2P(\text{Observing values more extreme than |t| }| \, \mu=\mu_0)

One-sample Two-sided t-test

p-value

  • p<0.05 means that the test statistic t is extreme: \,\, P(t_{n-1} > |t|)<0.025

  • t falls in the grey areas in the t_{n-1} plot below: Each grey area measures 0.025

One-sample Two-sided t-test

p-value

  • How to compute p?
    • Use statistical tables – Available here
    • Use R – Next sections

One-sample Two-sided t-test

Reference statistical tables

Find Table 13.1 in this file

  • Look at the row with Degree of Freedom n-1 (or its closest value)
  • Find critical value t^* := t_{n-1}(0.025) in column 0.025
  • Example: n=10, DF =9, t^*=t_{9}(0.025)=2.262

One-sample Two-sided t-test

Reference statistical tables

  • The critical value t^* = t_{n-1}(0.025) found in the table satisfies P(t_{n-1}>t^*) = 0.025

  • By definition of p-value for two-sided t-test we have p := 2P(t_{n-1}>|t|)

  • Therefore, for |t|>t^* \begin{align*} p & := 2P(t_{n-1}>|t|) \\ & < 2P(t_{n-1}>t^*) = 2 \cdot (0.025) = 0.05 \end{align*}

  • Conclusion: \quad |t|>t^* \iff p<0.05 \qquad (Extreme t \iff low p-value)

One-sample Two-sided t-test

Interpretation

Recall that p = 2P ( \text{Observing values more extreme than t } | \mu = \mu_0)

We have two possibilities:

  • |t|>t^*
    • In this case p<0.05
    • The observed statistic t is very unlikely under H_0 \,\, \implies \,\, reject H_0
  • |t| \leq t^*
    • In this case p>0.05
    • The observed statistic t is not unlikely under H_0 \,\, \implies \,\, do not reject H_0

Example: 2008 crisis

  • Data: Monthly Consumer Confidence Index (CCI) in 2007 and 2009
  • Question: Did the crash of 2008 have lasting impact upon CCI?
  • Observation: Data shows a massive drop in CCI between 2009 and 2007
  • Method: Use t-test to see if data is sufficient to prove that CCI actually dropped
Month J F M A M J J A S O N D
CCI 2007 86 86 88 90 99 97 97 96 99 97 90 90
CCI 2009 24 22 21 21 19 18 17 18 21 23 22 21
Difference 62 64 67 69 80 79 80 78 78 74 68 69

Example: 2008 crisis

  • This is really a two-sample problem – CCI data in 2 populations: 2007 and 2009
  • It reduces to a one-sample problem because we have directly comparable units
  • If units cannot be compared, then we must use a two-sample approach
  • Two-sample approach will be discussed later
Month J F M A M J J A S O N D
CCI 2007 86 86 88 90 99 97 97 96 99 97 90 90
CCI 2009 24 22 21 21 19 18 17 18 21 23 22 21
Difference 62 64 67 69 80 79 80 78 78 74 68 69

Example: 2008 crisis

Setting up the test

  • We want to test if there was a change in CCI from 2007 to 2009
  • We are really only interested in the difference in CCI
  • Let \mu be the (unknown) average difference in CCI
  • The null hypothesis is that there was (on average) no change in CCI H_0 \colon \mu = 0
  • The alternative hypothesis is that there was some change: H_1 \colon \mu \neq 0
  • Note that this is a two-sided test

Example: 2008 crisis

Calculation

Using the available data, we need to compute:

  • Sample mean and standard deviation \overline{x} = \frac{1}{n} \sum_{i=1}^n x_i \qquad s = \sqrt{\frac{\sum_{i=1}^n x_i^2 - n \overline{x}^2}{n-1}}

  • Test statistic t = \frac{\overline x - \mu_0}{s/\sqrt{n}}

Example: 2008 crisis

Calculation


CCI J F M A M J J A S O N D
Difference 62 64 67 69 80 79 80 78 78 74 68 69

\begin{align*} \overline{x} & =\frac{1}{n} \sum_{i=1}^{n} x_i=\frac{1}{12} \left(62+64+67+{\ldots}+68+69\right)=\frac{868}{12}=72.33 \\ \sum_{i=1}^{n} x_i^2 & = 62^2+64^2+67^2+{\ldots}+68^2+69^2 = 63260 \\ s & = \sqrt{ \frac{\sum_{i=1}^n x_i^2 - n \overline{x}^2}{n-1} } = \sqrt{\frac{63260-12\left(\frac{868}{12}\right)^2}{11}} = \sqrt{\frac{474.666}{11}} = 6.5689 \end{align*}

Example: 2008 crisis

Calculation

  • The sample size is n=12
  • The sample mean is \overline{x}=72.33
  • The sample standard deviation is s = 6.5689
  • The hypothesized mean is \mu_0 = 0
  • The t-statistic is t = \frac{\overline{x} - \mu_0}{s/\sqrt{n}} = \frac{72.33 - 0}{6.5689/\sqrt{12}} = 38.145

Example: 2008 crisis

Reference statistical tables

Find Table 13.1 in this file

  • Find row with DF = n-1 (or closest). Find critical value t^* in column 0.025
  • In our case: n=12, DF =11, t^*= t_{11}(0.025) =2.201

Example: 2008 crisis

Reference statistical tables

  • Plot of t_{11} distribution. White area is 0.95, total shaded area is 0.05
  • Probability of observing |t|>t^* = 2.201 is p<0.025

Example: 2008 crisis

Interpretation

  • We have computed:

    • Test statistic t = 38.145
    • Critical value t^* = 2.201

  • Therefore |t| = 38.145 > 2.201 = t^*

  • This implies rejecting the null hypothesis H_0 \colon \mu = 0

Example: 2008 crisis

Interpretation

  • t-test implies that mean difference in CCI is \mu \neq 0

  • The sample mean difference is positive (\bar{x}=72.33)

  • Conclusions:

    • CCI has changed from 2007 to 2009 (backed by t-test)
    • CCI seems higher in 2007 than in 2009 (backed by sample mean)
    • The 2008 crash seems to have reduced consumer confidence

Part 3:
The basics of R

What is R?

  • R is a high-level programming language (like Python)
  • This means R deals automatically with some details of computer execution:
    • Memory allocation
    • Resources allocation
  • R is focused on manipulating and analyzing data

References

Slides are based on

  • [1] Dalgaard, P.
    Introductory statistics with R
    Second Edition, Springer, 2008

  • [2] Davies, T.M.
    The book of R
    No Starch Press, 2016

Concise Statistics with R


Comprehensive R manual

Installing R on computer

  • R is freely available on Windows, Mac OS and Linux
  • To install:
    • Download R from CRAN https://cran.r-project.org
    • Make sure you choose the right version for your system
    • Follow the instructions to install

How to use R?

  • We have installed R. What now?

  • Launch the R Console. There are two ways:

    • Find the R application on your computer
    • Open a terminal, type R, exectute

Don’t have a laptop in class: Run R code in browser

R application

This is how the R Console looks on the Mac OS app

R from terminal

This is how the R Console looks on the Mac OS Terminal

What can R do?

  • R Console is waiting for commands
  • You can use the R Console interactively:
    • Type a command after the symbol >
    • Press Enter to execute
    • R will respond

Warning

  • The following slides might look like a lot of information
  • However you do not have to remember all the material
  • It is enough to:
    • Try to understand the examples
    • Know that certain commands exist and what they do
  • Combining commands to create complex codes comes with experience

Simple code can lead to impressive results

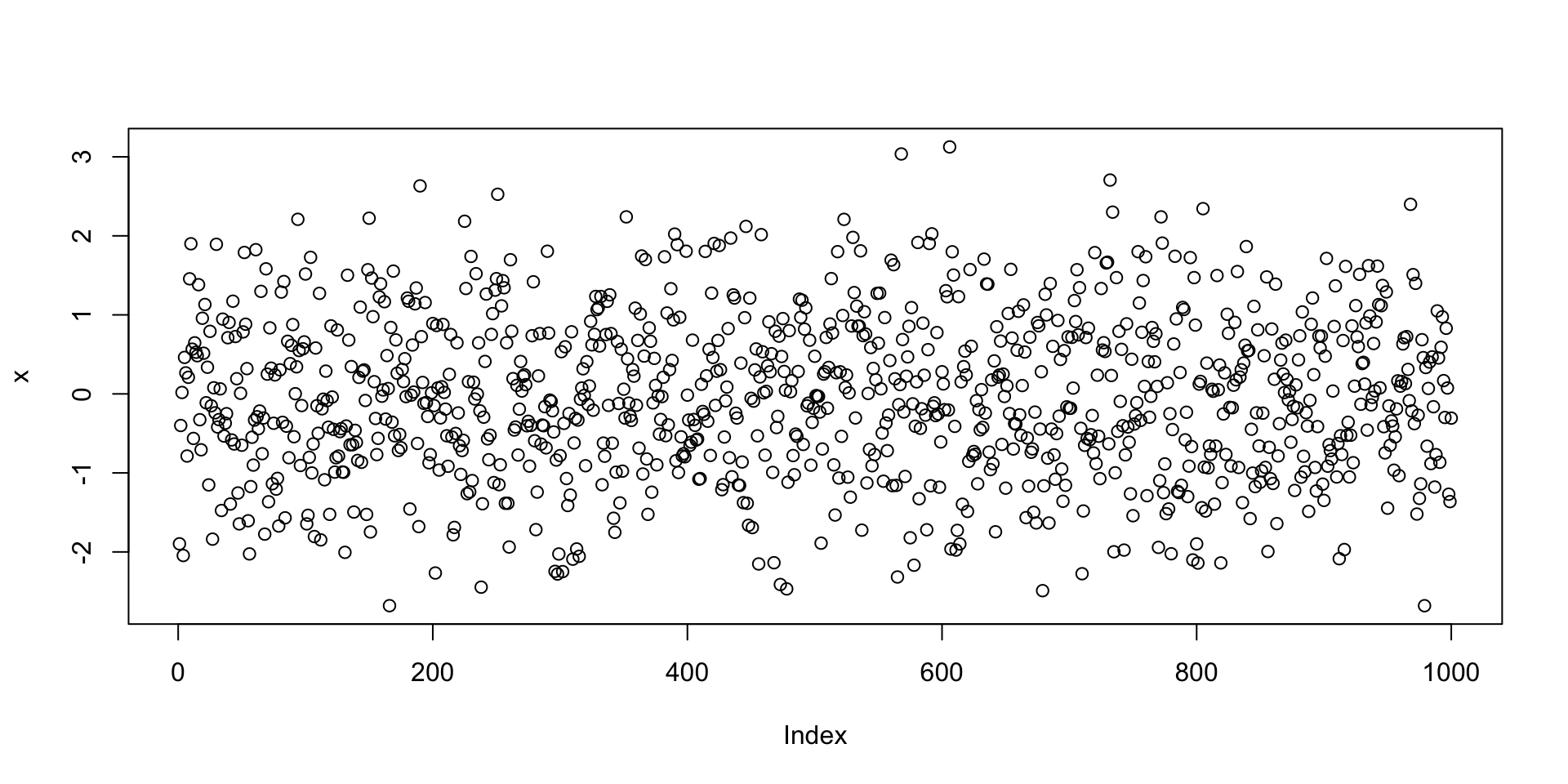
Example: Plotting 1000 values randomly generated from N(0,1) distribution

plot(rnorm(1000))

R as a calculator

R can perform basic mathematical operations

Below you can see R code and the corresponding answer

2 + 2
[1] 4
2 * 3 - 1 + 2 ^ 7
[1] 133
exp(-10)
[1] 4.539993e-05
log(2)
[1] 0.6931472
pi
[1] 3.141593
sin(pi/2)
[1] 1

R Scripts

  • The interactive R Console is OK for short codes

  • For longer code use R scripts

    • Write your code in a text editor
    • Save your code to a plain text file with .txt or .R extension
    • Execute your code in the R Console with source("file_name.R")

  • Examples of text editors

RStudio

  • RStudio is an alternative to R Console and text editors: Download here
    • RStudio is an Integrated Development Environment (IDE)
    • It is the R version of Spyder for Python
  • RStudio includes:
    • Direct-submission code editor
    • Separate point-and-click panes for files, objects, and project management
    • Creation of markup documents incorporating R code

Working Directory

R console

  • R session has a working directory associated with it

  • Unless specified, R will use a default working directory

  • To check the location of the working directory, use the getwd function

  • On my MacOS system I get \qquad

  • File paths are always enclosed in double quotation marks

  • Note that R uses forward slashes (not backslashes) for paths

  • You can change the default working directory using the function setwd

setwd("/folder1/folder2/folder3/")
  • File path can be relative to current working directory or full (system root drive)

Working Directory

RStudio

In RStudio you can set the working directory from the menu bar:

  • Session -> Set Working Directory -> Choose Directory

Comments

  • Good practice to document your code
  • This means adding comments directly in the code
  • Comments should be brief and explain what a chunk of code does
  • To insert a comment, preface the line with a hash mark #
# This is a comment in R
# Comments are ignored by R

1 + 1   # This works out the result of one plus one!
[1] 2

R Packages

  • The base installation of R comes ready with:
    • Commands for numeric calculations
    • Common statistical analyses
    • Plotting and visualization
  • More specialized techniques and data sets are contained in packages (libraries)
# To install a package, run
install.packages("package_name")

# To load a package into your code, type
library("package_name")

# To update all the packages currently installed, type
update.packages()

Help!

  • R comes with help files that you can use to search for particular functionality
  • For example you can check out how to precisely use a given function
  • To call for help type help(object_name)
help(mean)     # Mean is R function to compute average of some values

Further Help

  • Sometimes the output of help() can be cryptic
  • Seek help through Google
    • Qualify the search with R or the name of an R package
    • Paste an error message – chances are it is common error
  • Even better: Search engines specialized for R

Example: Plotting random numbers

Let us go back to the example of the command plot(rnorm(1000))

The function rnorm(n) outputs n randomly generated numbers from N(0,1)

rnorm(5)
[1] 0.6898848 0.4744542 1.2180847 0.8334529 0.6650749

The above values can be plotted by concatenating the plot command

plot(rnorm(5))

Note:

  • The values plotted (next slide) are, for sure, different from the ones listed above

  • This is because every time you call rnorm(5), new values are generated

  • We need to store the generated values if we want to re-use them (more later)

Example: Plotting random numbers

Variables and Assignments

  • Values can be stored (assigned) in symbolic variables or objects
  • The assignment operator in R is denoted by <-
    (an arrow pointing to the variable to which the value is assigned)

Example:

  • To assign the value 2 to the variable x, enter x <- 2
  • To recover the value in x, just type x
# Store 2 in the variable x
x <- 2

# Print x to screen
x
[1] 2

Variables and Assignments

Continuation of Example:

  • From now on, x has the value 2
  • The variable x can be used in subsequent operations
  • Such operations do not alter the value of x
# Assign 2 to x
x <- 2

# Compute x + x and print to screen
x + x
[1] 4
# x still contains 2
x
[1] 2

Example - Your first R code

  1. Open a text editor and copy paste the below code
# This codes sums two numbers and prints result on screen
x <- 1
y <- 2

result <- x + y

# Print the result on screen
cat("Code run successfully!")
cat("The sum of", x , "and", y, "is", result)

Example - Your first R code

  1. Save to a plain text file named either

    • my_first_code.R
    • my_first_code.txt

  2. Move this file to Desktop

  3. Open the R Console and change working directory to Desktop

# In MacOS type
setwd("~/Desktop")

# In Windows type
setwd("C:/Users/YourUsername/Desktop")

Example - Your first R code

  1. Run your code in the R Console by typying either
source("my_first_code.R")
source("my_first_code.txt")
  1. You should get the following output
Code run successfully!
The sum of 1 and 2 is 3

The workspace

  • Variables created in a session are stored in a Workspace
  • To display stored variables use
    • ls()
# Create 3 variables x, y, z
x <- 2
y <- "Dog"
z <- pi

# Workspace contains variables x, y, z
# This can be displayed by using ls()
ls()
[1] "x" "y" "z"

The workspace

You can remove variables from workspace by using

  • rm()
# Create 3 variables x, y, z
x <- 2
y <- "Dog"
z <- pi

# Remove x from workspace
rm(x)

# Now the workspace contains only y and z
ls( )
[1] "y" "z"

The workspace

To completely clear the workspace use

  • rm(list = ls())
# Create 3 variables x, y, z
x <- 2
y <- "Dog"
z <- pi

# Remove all variables from workspace
rm(list = ls())

# Let us check that the workspace is empty
ls( )
character(0)

Saving the Workspace

  • You can save the workspace using the command
    • save.image("file_name.RData")
  • The file file_name.RData
    • Is saved in the working directory
    • Contains all the objects currently in the workspace
  • You can load a saved workspace in a new R session with the command
    • load("file_name.RData")

Project Management

  • Recommended: keep all the files related to a project in a single folder

  • Such folder will have to be set as working directory in R Console

  • Saving the workspace could be dangerous

    • This is because R Console automatically loads existing saved workspaces
    • You might forget that this happens, and have undesired objects in workspace
    • This might lead to unintended results

  • Always store your code in R Scripts

Exiting R and Saving

To quit the R Console type q()

  • You will be asked if you want to save your session
  • If you say YES, the session will be saved in a .RData file in the working directory
  • Such file will be automatically loaded when you re-open the R Console
  • I recommend you DO NOT save your session

Exiting R and Saving

Summary

  • Write your code in R Scripts
  • These are .txt or .R text files
  • For later: Data should be stored in .txt files
  • DO NOT save your session when prompted

Part 4:
Vectors

Vectors

  • We saw how to store a single value in a variable
  • Series of values can be stored in vectors
  • Vectors can be constructed via the command c()
# Constuct a vector and store it in variable "vector"
vector <- c(60, 72, 57, 90, 95, 72)

# Print vector
print(vector)
[1] 60 72 57 90 95 72

Vectorized arithmetic

  • A vector is handled by R as a single object
  • You can do calculations with vectors, as long as they are of the same length
  • Important: Operations are exectuted component-wise
# Constuct two vectors of radius and height of 6 cylinders
radius <- c(6, 7, 5, 9, 9, 7)
height <- c(1.7, 1.8, 1.6, 2, 1, 1.9)

# Compute the volume of each cylinder and store it in "volume"
volume <- pi * radius^2 * height

# Print volume
print(volume)
[1] 192.2655 277.0885 125.6637 508.9380 254.4690 292.4823

Vectorized arithmetic

  • If 2 vectors do not have the same length then the shorter vector is cycled
  • This is called broadcasting
a <- c(1, 2, 3, 4, 5, 6, 7)
b <- c(0, 1)

a + b
[1] 1 3 3 5 5 7 7
  • In the example the vector a has 7 components while b has 2 components
  • The operation a + b is executed as follows:
    • b is copied 4 times to match the length of a
    • a + b is then obtained by a + \tilde{b} = (1, 2, 3, 4, 5, 6, 7) + (0, 1, 0, 1, 0, 1, 0) = (1, 3, 3, 5, 5, 7, 7)

Vectorized arithmetic

Useful applications of broadcasting are:

  • Multiplying a vector by a scalar
  • Adding a scalar to each component of a vector
vector <- c(1, 2, 3, 4, 5, 6)
scalar <- 2

# Multiplication of vector by a scalar
vector * scalar
[1]  2  4  6  8 10 12
# Summing a scalar to each component of a vector
vector + scalar
[1] 3 4 5 6 7 8

Sum and length

Two very useful vector operators are:

  • sum(x) which returns the sum of the components of x
  • length(x) which returns the length of x
x <- c(1, 2, 3, 4, 5)

sum <- sum(x)
length <- length(x)

cat("Here is the vector x:", x)
cat("The components of vector x sum to", sum)
cat("The length of vector x is", length)
Here is the vector x: ( 1 2 3 4 5 )
The components of vector x sum to 15
The length of vector x is 5

Computing sample mean and variance

Using vectorized operations

Given a vector \mathbf{x}= (x_1,\ldots,x_n) we want to compute sample mean and variance \overline{x} = \frac{1}{n} \sum_{i=1}^n x_i \,, \qquad s^2 = \frac{\sum_{i=1}^n (x_i - \overline{x})^2 }{n-1} 

# Computing sample mean of vector x
xbar = sum(x) / length(x)


# Computing sample variance of vector x
n = length(x)
s2 = sum( (x - barx)^2 ) / (n - 1)

Computing sample mean and variance

Using built in functions

  • R is a statistical language
  • There are built in functions to compute sample mean and variance:
    • mean(x) computes the sample mean of x
    • sd(x) computes the sample standard deviation of x
    • var(x) computes the sample variance of x

Exercise

Computing sample mean and variance

  • Let us go back to an Example we saw in Lecure 2
  • Below is the Wage data on 10 Mathematicians
Mathematician x_1 x_2 x_3 x_4 x_5 x_6 x_7 x_8 x_9 x_{10}
Wage 36 40 46 54 57 58 59 60 62 63
  • In Lecture 2, we have computed \overline{x} and s^2 by hand

Question:

  1. Enter the data into R
  2. Compute \overline{x} and s^2 using R

Solution

# First store the wage data into a vector
x <- c(36, 40, 46, 54, 57, 58, 59, 60, 62, 63)

# Compute the sample mean using formula
xbar = sum(x) / length(x)

# Compute the sample mean using built in R function
xbar_check = mean(x)

# We now print both results to screen
cat("Sample mean computed with formula is", xbar)
cat("Sample mean computed with R function is", xbar_check)
cat("They coincide!")
Sample mean computed with formula is 53.5
Sample mean computed with R function is 53.5
They coincide!

Solution

# Compute the sample variance using formula
xbar = mean(x)
n = length(x)
s2 = sum( (x - xbar)^2 ) / (n - 1) 

# Compute the sample variance using built in R function
s2_check = var(x)

# We now print both results to screen
cat("Sample variance computed with formula is", s2)
cat("Sample variance computed with R function is", s2_check)
cat("They coincide!")
Sample variance computed with formula is 90.27778
Sample variance computed with R function is 90.27778
They coincide!

Exercise

  • R contains some data sets by default, e.g. the data set rivers
    • This data set gives the lengths (in miles) of 141 major rivers in North America
  • For a vector x = (x_1,\ldots,x_n) \in \mathbb{R}^n, the average distance from the center is \frac{|x_1 - \bar{x}| + \ldots + |x_n - \bar{x}|}{n}\,, where \bar{x} = \frac{1}{n} \, \sum_{i=1}^n x_i is the mean of the vector x

Question: Compute the average distance from the center for the rivers data set

Hint: The absolute value of y \in \mathbb{R} is computed with abs(y)

Solution

To compute the average distance from the center for the rivers data set, we use the following R functions

  • mean
  • sum
  • abs
  • length
# Compute the average distance from the center for rivers
sum(abs(rivers - mean(rivers))) / length(rivers)    
[1] 313.5508

Part 5:
The t-test in R

The t-test in R

  • We are now ready to do some statistics in R
  • We start by looking at the one-sample t-test

Goal of t-test: Estimate the mean \mu of normal population N(\mu,\sigma^2)

Hypotheses: If \mu_0 is guess for \mu H_0 \colon \mu = \mu_0 \qquad H_1 \colon \mu \neq \mu_0

Method: Given the sample X_1 ,\ldots,X_n, we consider the statistic T = \frac{\overline{X}-\mu_0}{S/\sqrt{n}} \sim t_{n-1}

Reminder: The two-sided t-test by hand

  1. Given the data x_1,\ldots,x_n, compute the t-statistic t = \frac{\text{estimate } - \text{ hypothesised value}}{\mathop{\mathrm{e.s.e.}}} = \frac{\overline x - \mu_0}{s/\sqrt{n}} with sample mean and sample standard deviation \overline{x} = \frac{1}{n} \sum_{i=1}^n x_i \,, \qquad s = \sqrt{\frac{\sum_{i=1}^n x_i^2 - n \overline{x}^2}{n-1}}

  2. Find the critical value t^* = t_{n-1}(0.025) in Statistical Table 13.1

  • If |t|>t^* reject H_0. The mean is not \mu_0
  • If |t| \leq t^* do not reject H_0. There is not enough evidence

The t-test in R

  1. Given the sample x_1,\ldots,x_n, R can compute the t-statistic t = \frac{\text{estimate } - \text{ hypothesised value}}{\mathop{\mathrm{e.s.e.}}} = \frac{\overline x - \mu_0}{s/\sqrt{n}}

  2. R can compute the precise p-value (no need for Statistical Tables) p = 2P(|t_{n-1}|>t)

  • If p < 0.05 reject H_0. The mean is not equal to \mu_0
  • If p \geq 0.05 do not reject H_0. There is not enough evidence

Note: The above steps can be done simultaneously by using the command t.test

The t-test code in R

  1. Store the sample x_1,\ldots,x_n in an R vector using
    • data_vector <- c(x1, ..., xn)
  2. Perform a two-sided t-test on data_vector with null hypothesis mu0 using
    • t.test(data_vector, mu = mu0)
  3. Read the output. R will tell you
    • t-statistic
    • degrees of freedom
    • p-value
    • alternative hypothesis
    • confidence interval (where true mean is likely to be)
    • sample mean

Options of t.test command

  1. mu = mu0 tells R to test the hypothesis H_0 \colon \mu = \mu_0 \,, \qquad H_1 \colon \mu \neq \mu_0

  2. If mu = mu0 is not specified, R assumes \mu_0 = 0

  3. alternative = "greater" tells R to perform one-sided t-test H_0 \colon \mu \leq \mu_0 \,, \qquad H_1 \colon \mu > \mu_0

  4. alternative = "less" tells R to perform one-sided t-test H_0 \colon \mu \geq \mu_0 \,, \qquad H_1 \colon \mu < \mu_0

  5. conf.level = n changes the confidence interval level to n (default is 0.95)

Example: 2008 crisis

Let us go back to the 2008 Crisis example

  • Data: Monthly Consumer Confidence Index (CCI) in 2007 and 2009
  • Question: Did the crash of 2008 have lasting impact upon CCI?
  • Observation: Data shows a massive drop in CCI between 2009 and 2007
  • Method: Use t-test to see if data is sufficient to prove that CCI actually dropped
Month J F M A M J J A S O N D
CCI 2007 86 86 88 90 99 97 97 96 99 97 90 90
CCI 2009 24 22 21 21 19 18 17 18 21 23 22 21
Difference 62 64 67 69 80 79 80 78 78 74 68 69

Example: 2008 crisis

Setting up the test

  • We want to test if there was a change in CCI from 2007 to 2009

  • We interested in the difference in CCI

  • The null hypothesis is that there was (on average) no change in CCI H_0 \colon \mu = 0

  • The alternative hypothesis is that there was some change: H_1 \colon \mu \neq 0

Example: 2008 crisis

R code

# Enter CCI data in 2 vectors using function c()
score_2007 <- c(86, 86, 88, 90, 99, 97, 97, 96, 99, 97, 90, 90)
score_2009 <- c(24, 22, 21, 21, 19, 18, 17, 18, 21, 23, 22, 21)

# Compute vector of differences in CCI
difference <- score_2007 - score_2009

# Perform t-test on difference with null hypothesis mu = 0
# Store answer in "answer"
answer <- t.test(difference, mu = 0)

# Print the answer
print(answer)

Example: 2008 crisis

Output of t.test


    One Sample t-test

data:  difference
t = 38.144, df = 11, p-value = 4.861e-13
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 68.15960 76.50706
sample estimates:
mean of x 
 72.33333

Analysis of Output


    One Sample t-test
data:  difference


  • Description of the test that we have asked for
    • Note: t.test has automatically assumed that a one-sample test is desired
  • This also says which data are being tested
    • In our case we test the data in difference

Analysis of Output


t = 38.144, df = 11, p-value = 4.861e-13


This is the best part:

  • \texttt{t} = \, t-statistic from data
  • \texttt{df} = \, degrees of freedom
  • \texttt{p-value} = \, the exact p-value

Note:

  • You do not need Statistical Tables!
  • You see that p < 0.05
  • Therefore we reject null hypothesis that the mean difference is 0

Analysis of Output


alternative hypothesis: true mean is not equal to 0


  • R tells us the alternative hypothesis is \qquad H_1 \colon \mu \neq 0

  • Hence the Null hypothesis tested is \qquad \quad H_0 \colon \mu = 0

  • Warning:

    • This message is not telling you to accept to alternative hypothesis
    • This message is only stating the alternative hypothesis

Analysis of Output


95 percent confidence interval:
 68.15960 76.50706


95 \% confidence interval for the true mean \mu – an interval [a,b] s.t. P(\mu \in [a,b]) \geq 1 - \alpha = 0.95

Interpretation: If you repeat the experiment (on new data) over and over, the interval [a,b] will contain \mu about 95\% of the times

  • Confidence interval is not probability statement about \mu – note \mu is a constant!
  • It is probability statement about [a,b] – these are rv depending on the sample

Analysis of Output

Constructing the confidence interval for t-test:

  • Recall the t-statistic has t-distribution t = \frac{\overline{x}-\mu}{\mathop{\mathrm{e.s.e.}}} \, \sim \, t_{n-1}

  • We impose that t is observed with probability 1-\alpha P(- t^* \leq t \leq t^*) = 1-\alpha \,, \qquad t^* = t_{n-1}(\alpha/2)

  • The 1-\alpha confidence interval is obtained by solving for \mu P(\mu \in [a,b] ) = 1 - \alpha \,, \qquad a = \overline{x} - t^* \times \mathop{\mathrm{e.s.e.}}, \qquad b = \overline{x} + t^* \times \mathop{\mathrm{e.s.e.}}

Analysis of Output

  • To obtain 95\% confidence, we need \alpha = 0.05, so that 1-\alpha = 0.95

  • In this case the confidence interval is \left[ \overline{x} - t^* \times \mathop{\mathrm{e.s.e.}}, \overline{x} + t^* \times \mathop{\mathrm{e.s.e.}}\right] \,, \qquad t^* = t_{n-1}(0.025)

  • R calculated the above for us, giving the confidence interval \mu \in [68.15960, 76.50706]

Interpretation: If you repeat the experiment (on new data) over and over, the interval [a,b] will contain \mu about 95\% of the times

Analysis of Output


sample estimates:
mean of x 
 72.33333


  • This is the sample mean
  • You could have easily computed this with the code
    • mean(difference)

Conclusion

The key information is:

  • We conducted a two-sided t-test for the mean difference \mu \neq 0
  • Results give significant evidence p<0.05 that \mu \neq 0
  • The sample mean difference \overline{x} = 72.33333 \gg 0
  • This suggest CCI mean difference \mu \gg 0
  • Hence consumer confidence is higher in 2007 than in 2009

Exercise

SUV gas mileage

  • A consumer group wishes to see whether the actual mileage of a new SUV matches the advertised 17 miles per gallon

  • The group suspects it is lower

  • To test the claim, the group fills the SUV’s tank and records the mileage

  • This is repeated ten times. The results are below

11.4 13.1 14.7 14.7 15.0 15.5 15.6 15.9 16.0 16.8

Question: The data is assumed to be normal. Use R to test the claim H_0 \colon \mu = 17 \,, \qquad H_1 \colon \mu < 17

Solution

SUV gas mileage

This is a one-sided t-test. The p-value is computed as p = P( t_{n-1} < t \, | \, \mu = 17 ) 

# Enter the mileage data
mpg <- c(11.4, 13.1, 14.7, 14.7, 15.0, 15.5, 15.6, 15.9, 16.0, 16.8)

# Perform one-sided t-test with null hypothesis mu = 17 
# Store answer in "answer"
answer <- t.test(mpg, mu = 17, alternative = "less")

# Print the answer
print(answer)

Solution

SUV gas mileage


    One Sample t-test

data:  mpg
t = -4.2847, df = 9, p-value = 0.001018
alternative hypothesis: true mean is less than 17
95 percent confidence interval:
     -Inf 15.78127
sample estimates:
mean of x 
    14.87

Conclusion: The p-value is very small \quad p < 0.05 \quad \implies \quad reject H_0

  • The test discredits the claim of 17 miles per gallon
  • The SUV is less efficient than advertised

Part 6:
Graphics

Graphics

R has extensive built in graphing functions:

  • Fancier graphing functions are contained in the library ggplot2 (see link)

  • However we will be using the basic built in R graphing functions

Graphics

Scatter plot

  • Suppose given 2 vectors x and y of same length
  • The scatter plot of pairs (x_i,y_i) can be generated with plot(x, y)

Example: Suppose to have data of weights and heights of 6 people

  • To plot weight against height code is as follows
  • When you run plot() in R Console the plot will appear in a pop-up window
# Store weight and height data in 2 vectors
weight <- c(60, 72, 57, 90, 95, 72)
height <- c(1.75, 1.80, 1.65, 1.90, 1.74, 1.91)

# Plot weight against height
plot(weight, height)

Graphics

Graphics

Scatter plot – Options

  • You can customize your plot in many ways
  • Example: you can represent points (x_i,y_i) with triangles instead of circles
  • This can be done by including the command
    • pch = 2
  • pch stands for plotting character
# Store weight and height data in 2 vectors
weight <- c(60, 72, 57, 90, 95, 72)
height <- c(1.75, 1.80, 1.65, 1.90, 1.74, 1.91)

# Plot weight against height using little triangles
plot(weight, height, pch = 2)

Graphics

Graphics

Plotting 1D function f(x)

  • Create a grid of x values x = (x_1, \ldots, x_n)
  • Evaluate f on such grid. This yields a vector y = (f(x_1), \ldots, f(x_n))
  • Generate a scatter plot with
    • plot(x, y)
  • Use the function lines to linearly interpolate the scatter plot:
    • lines(x, y)

Graphics

Plotting functions - Example

Let us plot the parabola y = x^2 \,, \qquad x \in [-1,1] 

# Input vector for grid of x coordinates
x <- c(-1, -0.5, 0, 0.5, 1)

# Compute the function y=x^2 on the grid
y <- x^2

# Generate scatter plot of (x,y)
plot(x, y)

# Add linear interpolation
lines(x, y)

Graphics

Graphics

Plotting functions - Example

  • The previous plot was quite rough

  • This is because we only computed y=x^2 on the grid x = (-1, -0.5, 0, 0.5, 1)

  • We could refine the grid by hand, but this is not practical

  • To generate a finer grid we can use the built in R function

    • seq()

Seq function

seq(from, to, by, length.out) generates a vector containing a sequence:

  • from – The beginning number of the sequence
  • to – The ending number of the sequence
  • by – The step-size of the sequence (the increment)
  • length.out – The total length of the sequence

Example: Generate the vector of even numbers from 2 to 20

x <- seq(from = 2, to = 20, by = 2)
print(x)
 [1]  2  4  6  8 10 12 14 16 18 20

Seq function

Note: The following commands are equivalent:

  • seq(from = x1, to = x2, by = s)
  • seq(x1, x2, s)

Example: Generate the vector of odd numbers from 1 to 11

x <- seq(from = 1, to = 11, by = 2)
y <- seq(1, 11, 2)

cat("Vector x is: (", x, ")")
cat("Vector y is: (", y, ")")
cat("They are the same!")
Vector x is: ( 1 3 5 7 9 11 )
Vector y is: ( 1 3 5 7 9 11 )
They are the same!

Graphics

Plotting functions - Example

  • We go back to plotting y = x^2 \,, \qquad x \in [-1, 1]
  • We want to generate a grid, or sequece:
    • Starting at 0
    • Ending at 1
    • With increments of 0.2
x <- seq(from = -1, to = 1, by = 0.2)
print(x)
 [1] -1.0 -0.8 -0.6 -0.4 -0.2  0.0  0.2  0.4  0.6  0.8  1.0

Graphics

Plotting functions - Example

# Use seq() to generate x grid
x <- seq(from = -1, to = 1, by = 0.2)

# Plot the function y=x^2
plot(x, x^2)
lines(x, x^2)

Graphics

Scatter plot - Example

Let us go back to the example of plotting random normal values

  • First we generate a vector x with 1000 random normal values
  • Then we plot x via plot(x)
  • The command plot(x) implicitly assumes that:
    • x is the second argument: Values to plot on y-axis
    • The first argument is the vector seq(1, 1000)
    • Note that seq(1, 1000) is the vector of components numbers of x
x <- rnorm(1000)

plot(x)

Graphics

Part 7:
Functions in R

Expressions and objects

  • Basic way to interact with R is through expression evaluation:
    • You enter an epression
    • The system evaluates it and prints the result
  • Expressions work on objects
  • Object: anything that can be assigned to a variable
  • Objects encountered so far are:
    • Scalars
    • Vectors

Functions and arguments

  • Functions are a class of objects

  • Format of a function is name followed by parentheses containing arguments

  • Functions take arguments and return a result

  • We already encountered several built in functions:

    • plot(x, y)
    • lines(x, y)
    • seq(x)
    • print("Stats is great!")
    • cat("R is great!")
    • mean(x)
    • sin(x)

Functions and arguments

  • Functions have actual arguments and formal arguments
  • Example:
    • plot(x, y) has formal arguments two vectors x and y
    • plot(height, weight) has actual arguments height and weight
  • When you write plot(height, weight) the arguments are matched:
    • height corresponds to x-variable
    • weight corresponds to y-variable
    • This is called positional matching

Functions and arguments

  • If a function has a lot of arguments, positional matching is tedious

  • For example plot() accepts the following (and more!) arguments

Argument Description
x x coordinate of points in the plot
y y coordinate of points in the plot
type Type of plot to be drawn
main Title of the plot
xlab Label of x axis
ylab Label of y axis
pch Shape of points

Functions and arguments

Issue with having too many arguments is the following:

  • We might want to specify pch = 2
  • But then we would have to match all the arguments preceding pch
    • x
    • y
    • type
    • xlab
    • ylab

Functions and arguments

  • Thankfully we can use named actual arguments:
    • The name of a formal argument can be matched to an actual argument
    • This is independent of position
  • For example we can specify pch = 2 by the call
    • plot(weight, height, pch = 2)
  • In the above:
    • weight is implicitly matched to x
    • height is implicitly matched to y
    • pch is explicitly matched to 2
  • Note that the following call would give same output
    • plot(x = weight, y = height, pch = 2)

Functions and arguments

  • Named actual arguments override positional arguments
  • Example: The following commands yield the same plot
    • plot(height, weight)
    • plot(x = height, y = weight)
    • plot(y = weight, x = height)

Functions and arguments

We have already seen another example of named actual arguments

  • seq(from = 1, to = 11, by = 2)
  • seq(1, 11, 2)
  • These yield the same output. Why?
  • Because in this case named actual arguments match positional arguments

Functions and arguments

If however we want to divide the interval [1, 11] in 5 equal parts:

  • Have to use seq(1, 11, length.out = 6)
seq(1, 11, length.out = 6)
[1]  1  3  5  7  9 11
  • The above is different from seq(1, 11, 6)
seq(1, 11, 6)
[1] 1 7
  • They are different because:
    • The 3rd positional argument of seq() is by
    • Hence the command seq(1, 11, 6) assumes that by = 6

Functions and arguments

Warning

  • You can call functions without specifying arguments
  • However you have to use brackets ()
  • Example:
    • getwd() – which outputs current working directory
    • ls() – which outputs names of objects currently in memory

Custom functions

  • You can define your own functions in R
  • Syntax for definining custom function my_function is below
  • You can call your custom function by typing
    • my_function(arguments)
my_function <- function(first = "1st argument", 
                        ... ,
                        nth = "n-th argument") {
  
  # Code here: This is where you tell the function what to do

  return(object)      # Object to be returned  
}

Custom functions – Example

  • The R function mean(x) computes the sample mean of vector x

  • We want to define our own function to compute the mean

  • Example: The mean of x could be computed via

    • sum(x) / length(x)

  • We want to implement this code into the function my_mean(x)

    • my_mean takes vector x as argument
    • my_mean returns a scalar – the mean of x
# Definition of custom function my_mean(x)
my_mean <- function(vector = x) {
  
  mean_of_x <- sum(x) / length(x)
  
  return(mean_of_x)  
}

Custom functions – Example

  • Let us use our function my_mean on an example
# Generate a random vector of 1000 entries from N(0,1)
x <- rnorm(1000)

# Compute mean of x with my_mean
xbar <- my_mean(x)

# Compute mean of x with built in function mean
xbar_check <- mean(x)
  
cat("Mean of x computed with my_mean is:", xbar)
cat("Mean of x computed with R mean is:", xbar_check)
cat("They coincide!")
Mean of x computed with my_mean is: -0.01736574
Mean of x computed with R mean is: -0.01736574
They coincide!

Part 8:
More on Vectors

More on vectors

  • We have seen vectors of numbers
  • Further type of vectors are:
    • Character vectors
    • Logical vectors

Character vectors

  • A character vector is a vector of text strings
  • Elements are specified and printed in quotes
x <- c("Red", "Green", "Blue")
print(x)
[1] "Red"   "Green" "Blue"
  • You can use single- or double-quote symbols to specify strings
  • This is as long as the left quote is the same as the right quote
x <- c('Red', 'Green', 'Blue')
print(x)
[1] "Red"   "Green" "Blue"

Character vectors

Print and cat produce different output on character vectors:

  • print(x) prints all the strings in x separately
  • cat(x) concatenates strings. There is no way to tell how many were there
x <- c("Red", "Green", "Blue")
print(x)
cat(x)
[1] "Red"   "Green" "Blue" 
Red Green Blue
y <- c("Red Green", "Blue")
print(y)
cat(y)
[1] "Red Green" "Blue"     
Red Green Blue

Logical vectors

  • Logical vectors can take the values TRUE, FALSE or NA
  • TRUE and FALSE can be abbreviated with T and F
  • NA stands for not available
# Create logical vector
x <- c(T, T, F, T, NA)

# Print the logical vector
print(x)
[1]  TRUE  TRUE FALSE  TRUE    NA

Logical vectors

  • Logical vectors are extremely useful to evaluate conditions

  • Example:

    • given a numerical vector x
    • we want to count how many entries are above a value t
# Generate a vector containing sequence 1 to 8
x <- seq(from = 1 , to = 8, by = 1)

# Generate vector of flags for entries strictly above 5
y <- ( x > 5 )

cat("Vector x is: (", x, ")")
cat("Entries above 5 are: (", y, ")")
Vector x is: ( 1 2 3 4 5 6 7 8 )
Entries above 5 are: ( FALSE FALSE FALSE FALSE FALSE TRUE TRUE TRUE )

Logical vectors – Application

  • Generate a vector of 1000 numbers from N(0,1)
  • Count how many entries are above the mean 0
  • Since there are many (1000) entries, we expect a result close to 500
    • This is because sample mean converges to true mean 0

Question: How to do this?

Hint: T/F are interpreted as 1/0 in arithmetic operations

T + T
[1] 2
T + F
[1] 1
F + F
[1] 0
F + T + 3
[1] 4

Logical vectors – Application

  • The function sum(x) sums the entries of a vector x
  • We can use sum(x) to count the number of T entries in a logical vector x
x <- rnorm(1000)       # Generates vector with 1000 normal entries

y <- (x > 0)           # Generates logical vector of entries above 0

above_zero <- sum(y)   # Counts entries above zero

cat("Number of entries which are above the average 0 is", above_zero)
cat("This is pretty close to 500!")
Number of entries which are above the average 0 is 502
This is pretty close to 500!

Missing values

  • In practical data analysis, a data point is frequently unavailable
  • Statistical software needs ways to deal with this
  • R allows vectors to contain a special NA value - Not Available
  • NA is carried through in computations: operations on NA yield NA as the result
2 * NA
[1] NA
NA + NA
[1] NA
T + NA
[1] NA

Indexing vectors

  • Components of a vector can be retrieved by indexing

  • vector[k] returns k-th component of vector


vector <- c("Cat", "Dog", "Mouse")

second_element <- vector[2]           # Access 2nd entry of vector

print(second_element)
[1] "Dog"

Replacing vector elements

To modify an element of a vector use the following:

  • vector[k] <- value stores value in k-th component of vector


vector <- c("Cat", "Dog", "Mouse")

# We replace 2nd entry of vector with string "Horse"
vector[2] <- "Horse"

print(vector)
[1] "Cat"   "Horse" "Mouse"

Vector slicing

Returning multiple items of a vactor is known as slicing

  • vector[c(k1, ..., kn)] returns components k1, ..., kn
  • vector[k1:k2] returns components k1 to k2
vector <- c(11, 22, 33, 44, 55, 66, 77, 88, 99, 100)

# We store 1st, 3rd, 5th entries of vector in slice
slice <- vector[c(1, 3, 5)]   

print(slice)
[1] 11 33 55

Vector slicing

vector <- c(11, 22, 33, 44, 55, 66, 77, 88, 99, 100)

# We store 2nd to 7th entries of vector in slice
slice <- vector[2:7]

print(slice)
[1] 22 33 44 55 66 77

Deleting vector elements

  • Elements of a vector x can be deleted by using
    • x[ -c(k1, ..., kn) ] which deletes entries k1, ..., kn
# Create a vector x
x <- c(11, 22, 33, 44, 55, 66, 77, 88, 99, 100)

# Print vector x
cat("Vector x is:", x)

# Delete 2nd, 3rd and 7th entries of x
x <- x[ -c(2, 3, 7) ]

# Print x again
cat("Vector x with 2nd, 3rd and 7th entries removed:", x)
Vector x is: 11 22 33 44 55 66 77 88 99 100
Vector x with 2nd, 3rd and 7th entries removed: 11 44 55 66 88 99 100

Logical Subsetting

  • You can index or slice vectors by entering explicit indices
  • You can also index vectors, or subset, by using logical flag vectors:
    • Element is extracted if corresponding entry in the flag vector is TRUE
    • Logical flag vectors should be the same length as vector to subset

Code: Suppose given a vector x

  • Create a flag vector by using

    • flag <- condition(x)

  • condition() is any function which returns T/F vector of same length as x

  • Subset x by using

    • x[flag]

Logical Subsetting

Example

  • The following code extracts negative components from a numeric vector
  • This can be done by using
    • x[ x < 0 ]
# Create numeric vector x
x <- c(5, -2.3, 4, 4, 4, 6, 8, 10, 40221, -8)

# Get negative components from x and store them in neg_x
neg_x <- x[ x < 0 ]

cat("Vector x is:", x)
cat("Negative components of x are:", neg_x)
Vector x is: 5 -2.3 4 4 4 6 8 10 40221 -8
Negative components of x are: -2.3 -8

Logical Subsetting

Example

  • The following code extracts components falling between a and b
  • This can be done by using logical operator and &
    • x[ (x > a) & (x < b) ]
# Create numeric vector
x <- c(5, -2.3, 4, 4, 4, 6, 8, 10, 40221, -8)

# Get components between 0 and 100
range_x <- x[ (x > 0) & (x < 100) ]

cat("Vector x is:", x)
cat("Components of x between 0 and 100 are:", range_x)
Vector x is: 5 -2.3 4 4 4 6 8 10 40221 -8
Components of x between 0 and 100 are: 5 4 4 4 6 8 10

The function Which

  • which() allows to convert a logical vector flag into a numeric index vector
    • which(flag) is vector of indices of flag which correspond to TRUE
# Create a logical flag vector
flag <- c(T, F, F, T, F)

# Indices for  flag which
true_flag <- which(flag)

cat("Flag vector is:", flag)
cat("Positions for which Flag is TRUE are:", true_flag)
Flag vector is: TRUE FALSE FALSE TRUE FALSE
Positions for which Flag is TRUE are: 1 4

The function Which – Application

which() can be used to delete certain entries from a vector x

  • Create a flag vector by using

    • flag <- condition(x)

  • condition() is any function which returns T/F vector of same length as x

  • Delete entries flagged by condition using the code

    • x[ -which(flag) ]

The function Which – Application

Example

# Create numeric vector x
x <- c(5, -2.3, 4, 4, 4, 6, 8, 10, 40221, -8)

# Print x
cat("Vector x is:", x)

# Flag positive components of x
flag_pos_x <- (x > 0)

# Remove positive components from x
 x <- x[ -which(flag_pos_x) ]

# Print x again
cat("Vector x with positive components removed:", x)
Vector x is: 5 -2.3 4 4 4 6 8 10 40221 -8
Vector x with positive components removed: -2.3 -8

Functions that create vectors

The main functions to generate vectors are

  • c() concatenate
  • seq() sequence
  • rep() replicate

We have already met c() and seq() but there are more details to discuss

Concatenate

Recall: c() generates a vector containing the input values

# Generate a vector of values 1, 2, 3, 4, 5
x <- c(1, 2, 3, 4, 5)

# Print the vector
print(x)
[1] 1 2 3 4 5

Concatenate

  • c() can also concatenate vectors
  • This was you can add entries to an existing vector
# Create 2 vectors
x <- c(1, 2, 3, 4, 5)
y <- c(6, 7, 8)

# Concatenate vectors x and y, and also add element 9
z <- c(x, y, 9)

# Print the resulting vector
print(z)
[1] 1 2 3 4 5 6 7 8 9

Concatenate

  • You can assign names to vector elements

  • This modifies the way the vector is printed

# We specify a vector with 3 named entries
x <- c(first = "Red", second = "Green", third = "Blue")

# Print the named vector
print(x)
  first  second   third 
  "Red" "Green"  "Blue"

Concatenate

Given a named vector x

  • Names can be extracted with names(x)
  • Values can be extracted with unname(x)
# Create named vector
x <- c(first = "Red", second = "Green", third = "Blue")

# Access names of x via names(x)
names_x <- names(x)

# Access values of x via unname(x)
values_x <- unname(x)

cat("Names of x are:", names(x))
cat("Values of x are:", unname(x))
Names of x are: first second third
Values of x are: Red Green Blue

Concatenate

  • All elements of a vector have the same type
  • Concatenating vectors of different types leads to conversion
c(FALSE, 2)        # Converts FALSE to 0
[1] 0 2


c(pi, "stats")     # Converts pi to string 
[1] "3.14159265358979" "stats"           


c(TRUE, "stats")   # Converts TRUE to string
[1] "TRUE"  "stats"

Sequence

  • Recall the syntax of seq is
    • seq(from =, to =, by =, length.out =)
  • Omitting the third argument assumes that by = 1
# The following generates a vector of integers from 1 to 6
x <- seq(1, 6)

print(x)
[1] 1 2 3 4 5 6

Sequence

  • seq(x1, x2) is equivalent to x1:x2
  • Syntax x1:x2 is preferred to seq(x1, x2)
# Generate two vectors of integers from 1 to 6
x <- seq(1, 6)
y <- 1:6

cat("Vector x is:", x)
cat("Vector y is:", y)
cat("They are the same!")
Vector x is: 1 2 3 4 5 6
Vector y is: 1 2 3 4 5 6
They are the same!

Replicate

rep generates repeated values from a vector:

  • x vector
  • n integer
  • rep(x, n) repeats n times the vector x
# Create a vector with 3 components
x <- c(2, 1, 3)

# Repeats 4 times the vector x
y <- rep(x, 4)

cat("Original vector is:", x)
cat("Original vector repeated 4 times:", y)
Original vector is: 2 1 3
Original vector repeated 4 times: 2 1 3 2 1 3 2 1 3 2 1 3

Replicate

The second argument of rep() can also be a vector:

  • Given x and y vectors
  • rep(x, y) repeats entries of x as many times as corresponding entries of y
x <- c(2, 1, 3)         # Vector to replicate
y <- c(1, 2, 3)         # Vector saying how to replicate 

z <- rep(x, y)          # 1st entry of x is replicated 1 time
                        # 2nd entry of x is replicated 2 times
                        # 3rd entry of x is replicated 3 times

cat("Original vector is:", x)
cat("Original vector repeated is:", z)
Original vector is: 2 1 3
Original vector repeated is: 2 1 1 3 3 3

Replicate

  • rep() can be useful to create vectors of labels
  • Example: Suppose we want to collect some numeric data on 3 Cats and 4 Dogs
x <- c("Cat", "Dog")     # Vector to replicate

y <- rep(x, c(3, 4))     # 1st entry of x is replicated 3 times
                         # 2nd entry of x is replicated 4 times

cat("Vector of labels is:", y)
Vector of labels is: Cat Cat Cat Dog Dog Dog Dog

References

Homepage      License      Contact

[1]
Dalgaard, Peter, Introductory statistics with R, Second Edition, Springer, 2008.
[2]
Davies, Tilman M., The book of R, No Starch Press, 2016.